Координаты вектора

Определение

Векторы называются компланарными , если при откладывании их из одной и той же точки они будут лежать в одной плоскости .

Определение

z

1

y

1

0

1

x

z

1

y

1

0

1

x

z

Задача.

5

Дано :

B

T

AODMPBTC –

прямоугольный параллелепипед

P

C

ОА = 2, О D = 3, О B = 5, МК = 1

Определить:

координаты векторов : c

3

O

D

y

2

M

A

К

x

z

Задача.

5

Дано :

B

T

AODMPBTC –

прямоугольный параллелепипед

P

C

ОА = 2, О D = 3, О B = 5, МК = 1.

Определить:

координаты векторов :

O

D

D

y

Решение:

2

z = О B = 5

у = О D = 3 ;

х = ОА = 2 ;

M

A

К

x

z

Задача.

5

Дано :

B

T

AODMPBTC –

прямоугольный параллелепипед

C

P

ОА = 2, О D = 3, О B = 5, МК = 1.

Определить:

координаты векторов :

O

D

D

y

Решение:

2

z = О B = 5

у = О D = 3 ;

х = ОА = 2 ;

M

A

у = О D = 3

х = ОА = 2 ;

z = МК = -1;

К

x

z

Задача.

5

Дано :

B

T

AODMPBTC –

прямоугольный параллелепипед

P

C

ОА = 2, О D = 3, О B = 5, МК = 1.

Определить:

координаты векторов :

O

D

D

y

Решение:

2

z = О B = 5

у = О D = 3 ;

х = ОА = 2 ;

M

A

у = О D = 3

х = ОА = 2 ;

z = МК = -1;

К

x

у = О D = 3 ;

z = 0

х = ОА = 2 ;

z

Задача.

5

Дано :

B

T

AODMPBTC –

прямоугольный параллелепипед

P

C

ОА = 2, О D = 3, О B = 5, МК = 1.

Определить:

координаты векторов :

O

D

D

y

Решение:

2

z = О B = 5

у = О D = 3 ;

х = ОА = 2 ;

M

A

у = О D = 3

х = ОА = 2 ;

z = МК = -1;

К

x

у = О D = 3 ;

z = 0

х = ОА = 2 ;

z

Задача.

5

Дано :

B

T

AODMPBTC –

прямоугольный параллелепипед

P

C

ОА = 2, О D = 3, О B = 5, МК = 1.

Определить:

координаты векторов :

O

D

D

y

Решение:

2

z = О B = 5

у = О D = 3 ;

х = ОА = 2 ;

M

A

у = О D = 3

х = ОА = 2 ;

z = МК = -1;

К

x

у = О D = 3 ;

z = 0

х = ОА = 2 ;

z

Задача.

5

Дано :

B

T

AODMPBTC –

прямоугольный параллелепипед

P

C

ОА = 2, О D = 3, О B = 5, МК = 1.

Определить:

координаты векторов :

O

D

D

y

Решение:

2

z = О B = 5

у = О D = 3 ;

х = ОА = 2 ;

M

A

у = О D = 3

х = ОА = 2 ;

z = МК = -1;

К

x

у = О D = 3 ;

z = 0

х = ОА = 2 ;

z

Задача.

5

Дано :

B

T

AODMPBTC –

прямоугольный параллелепипед

P

C

ОА = 2, О D = 3, О B = 5, МК = 1.

Определить:

координаты векторов :

O

D

D

y

Решение:

2

z = О B = 5

у = О D = 3 ;

х = ОА = 2 ;

M

A

у = О D = 3

х = ОА = 2 ;

z = МК = -1;

К

x

у = О D = 3 ;

z = 0

х = ОА = 2 ;

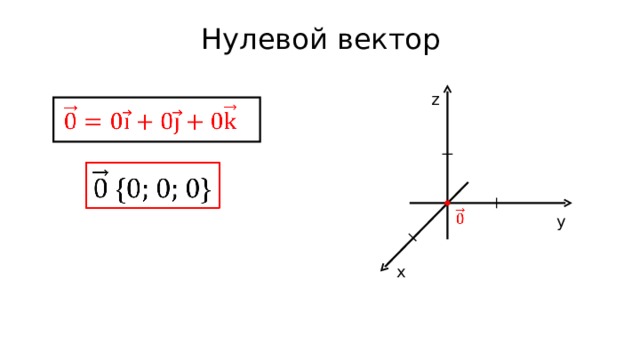
Нулевой вектор

z

y

х

Координаты равных векторов соответственно равны.

х₁ = х₂, у₁ = у₂, z ₁ = z ₂

Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов.

Каждая координата разности двух векторов равна разности соответствующих координат этих векторов.

Каждая координата произведения

вектора на число равна произведению соответствующей координаты вектора на это число.

Задача 1.

Дано:

Найти :

Решение :

х = 2 + 0 – 2 = 0

у = – 4 – 1 + 3 = – 2

z = 0 + 2 + 1 = 3

Задача 2.

Дано:

Решение :