Лекция №1
Тема: Көптүктөр жөнүндө түшүнүк
XIX кылымдын аяндагы математика илиминде функция, үзгүлтүксүздүк ж.б.у.с. негизги түшүнүктөрдү тактоо зарылдыгы келип чыккан. Бул үчүн натуралдык сан түшүнүгүн так аныктоо керек болгон. Мына ушундай татаал суроолорго жооп издөө математикалык идеялардын өнүгүшүнө мүмкүндүк түзгөн. Ошондуктан, XIX кылымдын аягында XXI кылымдын башында математикалык билимдердин бардык тармактарында эски түшүнүктөр кайрадан каралып, такталып чыккан. Натыйжада, XIX кылымдын аягында математиканын жаңы тармагы – көптүктөр теориясы пайда болгон. Анын түзүүчүлөрүнүн бири - немец окумуштуусу Георг Кантор (1845-1918) болгон. Кыска мөөнөттүн ичинде көптүктөр теориясы бүтүндөй математиканын пайдубалы болуп калды.
Көптүк түшүнүгү – математиканын алгачкы түшүнүктөрүнүн бири болуп эсептелет, б.а. ал башка түшүнүктөр аркылуу аныкталбайт, бирок түшүндүрүү жолу менен баяндалат.
Көптүк деп кандайдыр бир объекттердин жыйындысын түшүнөбүз. Мисалы, бүтүн сандардын жыйндысы, латын алфавитинин тамгалары, университеттеги студенттер, асмандагы жылдыздар, дарыялар, көлдөр, тоолор, автоунаалар ж.б. обьекттер көптүк түшүнүгүнө мисал боло алат. Мындан, көптүктү түзгөн обьекттердин жаратылышынын ар түрдүүлүгүн жана көптүктөр теориясынын колдонулушунун кеңири экендигин байкайбыз.
Көптүктү түзгөн объекттер көптүктүн элементтери деп аталат. Демек, ар бир көптүк элементтерден турат. Элементтеринин саны чектүү болгон көптүктү чектүү көптүк деп, ал эми элементтеринин саны чексиз болгон көптүктү чексиз көптүк деп айтабыз.
Көптүктөр латын алфавитинин чоң тамгалары менен, ал эми элементтери латын алфавитинин кичине
тамгалары менен, ал эми элементтери латын алфавитинин кичине  тамгалары менен белгиленет. Көптүктүн элементтери фигуралык кашаалардын ичине жазылып, бири-биринен үтүр аркылуу ажыралат:
тамгалары менен белгиленет. Көптүктүн элементтери фигуралык кашаалардын ичине жазылып, бири-биринен үтүр аркылуу ажыралат:
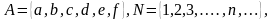
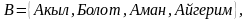
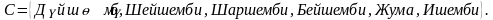
Көптүктөрдүн жана алардын элементтерин башка алфавиттердин тамгалары менен да белгилөөгө болот.
Көптүктөрдүн берилүү жолдору
Көптүктөрдү эки түрдүү жол менен берүүгө болот: 1) элементтерин саноо жолу; 2) элементтеринин касиетин баяндоо (мүнөздөө) жолу менен.
Жогорудагы мисалда  көптүктөрү көптүктүн элементтерин саноо жолу, б.а. 1-жол менен берилди.
көптүктөрү көптүктүн элементтерин саноо жолу, б.а. 1-жол менен берилди.
Көптүктүн элементтеринин касиеттерин баяндоо жолу менен, б.а. 2-жол менен берүү төмөнкүдөй болот. Эгерде  көптүгүнүн бардык элементтери
көптүгүнүн бардык элементтери 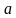 касиетин канааттандырса, анда
касиетин канааттандырса, анда  көптүгүн төмөнкүдөй жазабыз:
көптүгүн төмөнкүдөй жазабыз: 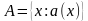 .
.
Мисалы, 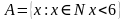 көптүгү элементтеринин касиетин баяндоо жолу менен берилди. Чындыгында бул көптүк
көптүгү элементтеринин касиетин баяндоо жолу менен берилди. Чындыгында бул көптүк 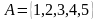 көптүгү менен дал келет.
көптүгү менен дал келет.
Мындан тышкары көптүктү баяндоодо анын элементтеринин көптүгү эске алынбайт. Көптүктү баяндоо жолу менен берүү айрыкча көптүктөрдүн үстүнөн амал жүргүзүүдо ыңгайлуу болот. Кээ бир стандарттык негизги көпртүктор үчун атайын белгилөөлөр кабыл алынган, мисалы: N, Z, Q, R, C ж.б.у.с., алар:
N - натуралдык сандардын көптүгү,
Z - бүтүн сандардын көптүгү,
Q - рационалдык сандардын көптүгү,
R - чыныгы (анык) сандардын көптүгү,
C - комплекстик сандардын көптүгү,
 -
-  сегментинде үзгүлтүксүз болгон фнукциялардын көптүгү.
сегментинде үзгүлтүксүз болгон фнукциялардын көптүгү.
Жогорудагы мисалда элементтеринин саны чектүү болгондуктан A,B,C көптүктөрү чектүү көптүктөр, ал эми элементтеринин саны чексиз болгондуктан N көптүгү чексиз көптүк болуп эсептелет.
Бир да элементи жок болгон көптүктү бош (куру) көптүк деп атайбыз жана аны  символу менен белгилейбиз. Мисалы,
символу менен белгилейбиз. Мисалы, 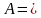 {Жер шаарынын айланасында айланып жүргөн планеталар},
{Жер шаарынын айланасында айланып жүргөн планеталар},  {Биринчи класстын окуучуларынын арасында боюнун узундугу 2 метр болгон окуучулар} – көптүктөрү бош көптүктөргө мисал боло алат.
{Биринчи класстын окуучуларынын арасында боюнун узундугу 2 метр болгон окуучулар} – көптүктөрү бош көптүктөргө мисал боло алат.
х элементи Х көптүгүнө таандык (же тиешелүү) дегенди  аркылуу белгилейбиз. Эгерде х элементи Х көптүгүнө таандык эмес дегенди
аркылуу белгилейбиз. Эгерде х элементи Х көптүгүнө таандык эмес дегенди  (же
(же  ) деп жазабыз.
) деп жазабыз.
Эгерде А көптүгүнүн бардык элементтери В көптүгүнүн да элементтери болсо, анда А көптүгү В көптүгүнүн бөлүкчө(камтылуучу) көптүгү деп аталат жана төмөндөгүдөй жазылат: 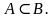 Мында “
Мында “ ” символу көптүктөрдүн камтылуусун түшүндүрөт. Бош көптүк каалаган көптүктүн бөлүкчө көптүгү болот, б.а.
” символу көптүктөрдүн камтылуусун түшүндүрөт. Бош көптүк каалаган көптүктүн бөлүкчө көптүгү болот, б.а. 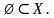
Мисалы, 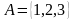 жана
жана  көптүктөрү берилсе, анда
көптүктөрү берилсе, анда  болот, себеби А көптүгүнүн элементтери В көптүгүндө табылат.
болот, себеби А көптүгүнүн элементтери В көптүгүндө табылат.
Камтылуучулук төмөндөгүдөй касиеттерге ээ:
а) 
б)
в)
Кээде көптүктүн элементтери да көптүк болушу мүмкүн. Мисалы,  көптүгү университеттин 4-курсунун студенттик тайпаларынын көптүгү болсун. Бул учурда студенттик тайпалардын ар бири өз учурунда көптүктөрдү түзүшөт. Мындан, көптүктүн бир нече бөлүкчө көптүктөрүнүн жашай тургандыгын байкайбыз.
көптүгү университеттин 4-курсунун студенттик тайпаларынын көптүгү болсун. Бул учурда студенттик тайпалардын ар бири өз учурунда көптүктөрдү түзүшөт. Мындан, көптүктүн бир нече бөлүкчө көптүктөрүнүн жашай тургандыгын байкайбыз.
Эгерде  көптүгүнүн ар бир элементи бир эле учурда
көптүгүнүн ар бир элементи бир эле учурда  көптүгүнүн элементи болсо жана тескерисинче B көптүгүнүн ар бир элементи A көптүгүнүн элементи болсо, анда А жана В көптүктөрү барабар деп аталат жана төмөнкүдөй жазылат: А=В.
көптүгүнүн элементи болсо жана тескерисинче B көптүгүнүн ар бир элементи A көптүгүнүн элементи болсо, анда А жана В көптүктөрү барабар деп аталат жана төмөнкүдөй жазылат: А=В.
Мисалы,  жана
жана  көптүктөрү бирдей элементтерден тургандыктан алар барабар болот.
көптүктөрү бирдей элементтерден тургандыктан алар барабар болот.
Эгерде  болсо, анда А көптүгү В көптүгүнүн өздүк камтылуучу көптүгү деп аталат.
болсо, анда А көптүгү В көптүгүнүн өздүк камтылуучу көптүгү деп аталат.
Эгерде А жана В көптүктөрүнүн арасында өз ара бир маанилүү тиешелештик орнотулса, анда алар эквиваленттүү деп аталышат жана  деп белгиленет.
деп белгиленет.
Чектүү көптүктөрдүн эквиваленттүүлүгү алардын бирдей сандагы элементтерден тураарын түшүндүрөт. Ошондуктан, бир да чектүү көптүк өзүнүн өздүк камтылуучусу менен эквиваленттүү боло албайт. Бирок чексиз көптүктөр өздөрүнүн өздүк камтылуучулары менен эквиваленттүү болуп калышы мүмкүн. Мисалы, болсо,  болот.
болот.
Натуралдык сандардын көптүгүно эквиваленттүү болгон көптүк санаттык көптүк деп аталат.
Универсалдык (негизги) көптүк деп каралып жаткан көптүктөрдү камтып турган көптүктү айтабыз жана аны U тамгасы менен белгилейбиз.
Мисалы, R чыныгы сандардын көптүгү Q рационалдык жана J иррационалдык сандардын көптүктөрү үчүн универсалдык көптүк болот, б.а. U=R.
Текшерүүчү суроолор:
Көптүккө эмне үчүн аныктама берилбейт?
Камтылуучу көптүк деп кандай көптүктү айтабыз?
Кандай эки көптүк барабар болот?
Эквиваленттүу көптүктөр деген кандай көптүктөр?
Көптүктөрдү кантип салыштырабыз?
Санаттык эмес көптүккө аныктама берип, мисал келтиргиле.







 тамгалары менен, ал эми элементтери латын алфавитинин кичине
тамгалары менен, ал эми элементтери латын алфавитинин кичине  тамгалары менен белгиленет. Көптүктүн элементтери фигуралык кашаалардын ичине жазылып, бири-биринен үтүр аркылуу ажыралат:
тамгалары менен белгиленет. Көптүктүн элементтери фигуралык кашаалардын ичине жазылып, бири-биринен үтүр аркылуу ажыралат: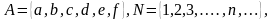
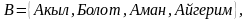
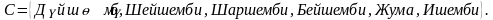
 көптүктөрү көптүктүн элементтерин саноо жолу, б.а. 1-жол менен берилди.
көптүктөрү көптүктүн элементтерин саноо жолу, б.а. 1-жол менен берилди. көптүгүнүн бардык элементтери
көптүгүнүн бардык элементтери 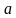 касиетин канааттандырса, анда
касиетин канааттандырса, анда 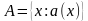 .
.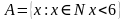 көптүгү элементтеринин касиетин баяндоо жолу менен берилди. Чындыгында бул көптүк
көптүгү элементтеринин касиетин баяндоо жолу менен берилди. Чындыгында бул көптүк 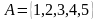 көптүгү менен дал келет.
көптүгү менен дал келет. -
-  сегментинде үзгүлтүксүз болгон фнукциялардын көптүгү.
сегментинде үзгүлтүксүз болгон фнукциялардын көптүгү. символу менен белгилейбиз. Мисалы,
символу менен белгилейбиз. Мисалы, 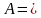 {Жер шаарынын айланасында айланып жүргөн планеталар},
{Жер шаарынын айланасында айланып жүргөн планеталар},  {Биринчи класстын окуучуларынын арасында боюнун узундугу 2 метр болгон окуучулар} – көптүктөрү бош көптүктөргө мисал боло алат.
{Биринчи класстын окуучуларынын арасында боюнун узундугу 2 метр болгон окуучулар} – көптүктөрү бош көптүктөргө мисал боло алат. аркылуу белгилейбиз. Эгерде х элементи Х көптүгүнө таандык эмес дегенди
аркылуу белгилейбиз. Эгерде х элементи Х көптүгүнө таандык эмес дегенди  (же
(же  ) деп жазабыз.
) деп жазабыз.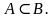 Мында “
Мында “ ” символу көптүктөрдүн камтылуусун түшүндүрөт. Бош көптүк каалаган көптүктүн бөлүкчө көптүгү болот, б.а.
” символу көптүктөрдүн камтылуусун түшүндүрөт. Бош көптүк каалаган көптүктүн бөлүкчө көптүгү болот, б.а. 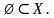
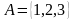 жана
жана  көптүктөрү берилсе, анда
көптүктөрү берилсе, анда 









