Корень n-й степени и свойства

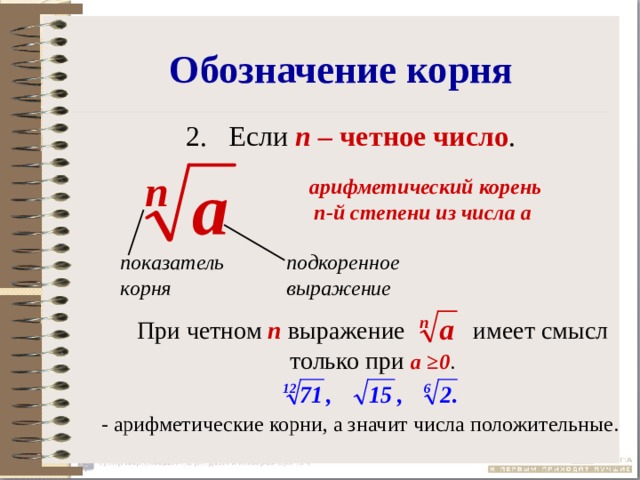
Обозначение корня

• Если n – нечетное число .

Если а ≥0 , то - арифметический корень n-й степени из числа а .

корень n-й степени из числа а

(положительного, отрицательного или нуля).

показатель

подкоренное

выражение

корня

корень5-й

арифметический корень

степени из 12

3-й степени из 7

арифметический корень

5-й степени из 12

Обозначение корня

• Если n – четное число .

При четном n выражение имеет смысл только при а ≥0 .

арифметический корень

n-й степени из числа а

подкоренное

показатель

выражение

корня

- арифметические корни, а значит числа положительные.

Корень n -й степени

• Во множестве действительных чисел существует единственный корень нечетной степени n из любого числа а . ( ).

• Во множестве действительных чисел существует два корня четной степени n из любого положительного числа а , их модули равны, а знаки противоположны.

Свойства корней n -й степени

Когда n – нечетное , то при любом значении а верно равенство

Когда n – четное , то при

любом положительном

значении а верно

равенство

Свойства корней n-й степени

Теорема .

Пусть n

Пусть n

- нечетное число .

- четное число .

Тогда при любом значении а верны равенства:

Свойства корней n -й степени

Теорема . Пусть n и k - натуральные числа. Тогда при любом неотрицательном значении а верны равенства:

(При извлечении корня из корня подкоренное выражение остается прежним, а показатели корней перемножаются.)

Сравнить числа и .

Свойства корней n -й степени

Теорема . Пусть k – целое число. Тогда при любом положительном значении а верно равенство:

Решить уравнение:

Решение.

Тогда

Ответ: 64 ; 117 649 .

Свойства корней n -й степени

Теорема .

Пусть n – нечетное число .

Тогда при любых значениях

а и b верно равенство

Пусть n – четное число . Тогда при любых а ≥ 0 и b ≥ 0 верно равенство

0 верно равенство " width="640"

Свойства корней n -й степени

Теорема .

Пусть n – нечетное число .

Тогда при любых значениях

а и b ≠ 0 верно равенство

Пусть n – четное число . Тогда при любых а ≥ 0 и b 0 верно равенство

Свойства корней n-й степени

Теорема .

Пусть n – нечетное число .

Тогда при любых значениях

а и b верно равенство

Пусть n – четное число . Тогда при любых значениях

а и b ≥ 0 верно равенство

Вынесение множителя из-под знака корня

Преобразование выражения к виду называется вынесением множителя из-под знака корня нечетной степени .

Преобразование выражения к виду называется вынесением множителя из-под знака корня четной степени .

Внесение множителя под знак корня

Преобразование выражения к виду называется внесением множителя под знак корня нечетной степени .

Преобразование выражения к виду называется внесением множителя под знак корня четной степени .

1 – нечетное число; а 1 , а 2 , … , а k - любые числа. Пусть n ≥ 2 – четное число; а 1 , а 2 , … , а k - любые неотрицательныые числа. Корень n-й степени из произведения нескольких чисел равен произведению корней n-й степени из этих чисел. В частности, пологая в этом равенстве а 1 = а 2 = … = а k = а , получим " width="640"

Свойства корней n-й степени

Теорема.

Пусть n 1 – нечетное число; а 1 , а 2 , … , а k - любые числа.

Пусть n ≥ 2 – четное число;

а 1 , а 2 , … , а k - любые

неотрицательныые числа.

Корень n-й степени из произведения нескольких чисел

равен произведению корней n-й степени из этих чисел.

В частности, пологая в этом равенстве

а 1 = а 2 = … = а k = а , получим

Свойства корней n -й степени

n – нечетное число

n – четное число

при любом а

при а ≥ 0

при любом а

при любом а

при любом а

при а = 0

при любых

при любых

если а и b

а и b

одного знака

а и b

при а ≥ 0

и b ≥ 0

0 " width="640"

Свойства корней n -й степени

n – нечетное число

n – четное число

при любых

а и b

при а ≥ 0

и b ≥ 0

при а

при любых

а и b

при любом

и b ≥ 0

при любых

а и b ≥ 0

при любых

а и b ≠ 0

если а и b одного

при а ≥ 0

а и b ≠ 0

знака и b ≠ 0

и b 0

Свойства корней n -й степени

При любых натуральных значениях n ≥ 2

и k ≥ 2 для а ≥ 0 имеют место тождества: