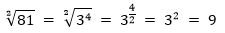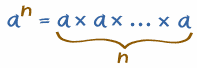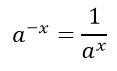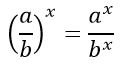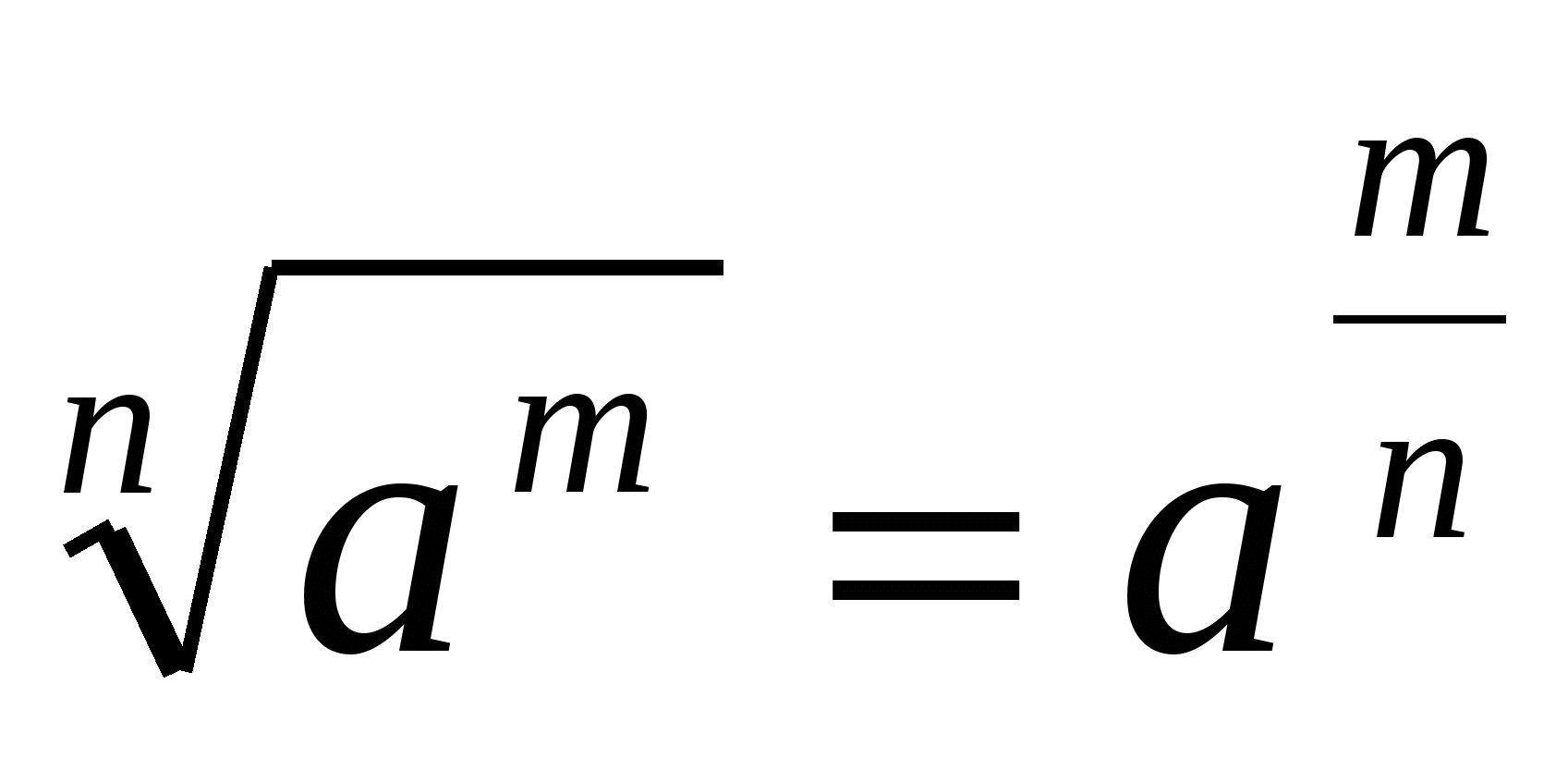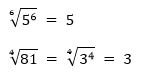Корни и степени

Корни и степени

Свойства степени с действительным показателем

Под степенью некоторого числа "а" с некоторым показателем "n" понимают произведение числа "а" само на себя "n" раз.

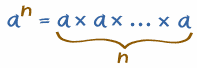
Если в основании степени лежит положительное число, а в качестве показателя используются действительные числа, то можно пользоваться следующими формулами:

1. Так как в основании степени используется положительное число, то, несмотря на знак показателя степени, результат всегда будет числом положительным.

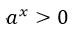
2. Если показатель степени является отрицательным числом, то его можно заменить на равный по модулю положительный показатель, а основание дроби перевернуть.

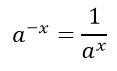
3. При умножении чисел с одинаковыми основаниями, действительные показатели степени следует сложить.

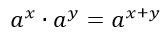
4. При делении чисел с одинаковыми основаниями, действительные показатели степени вычитаются:

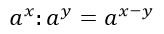
5. При возведении числа в степени в дополнительную степень показатели умножаются.

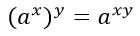
6. При возведении произведения некоторых чисел в действительную степень можно возвести каждое число по отдельности в данную степень и только после этого перемножить.

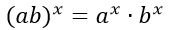
7. При возведении частного некоторых чисел в действительную степень можно возвести каждое число по отдельности в данную дробь и только после этого разделить.

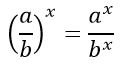
Степень с рациональным показателем

Степень с рациональным показателем - это та, в показателе которой находится конечная обыкновенная или десятичная дробь.

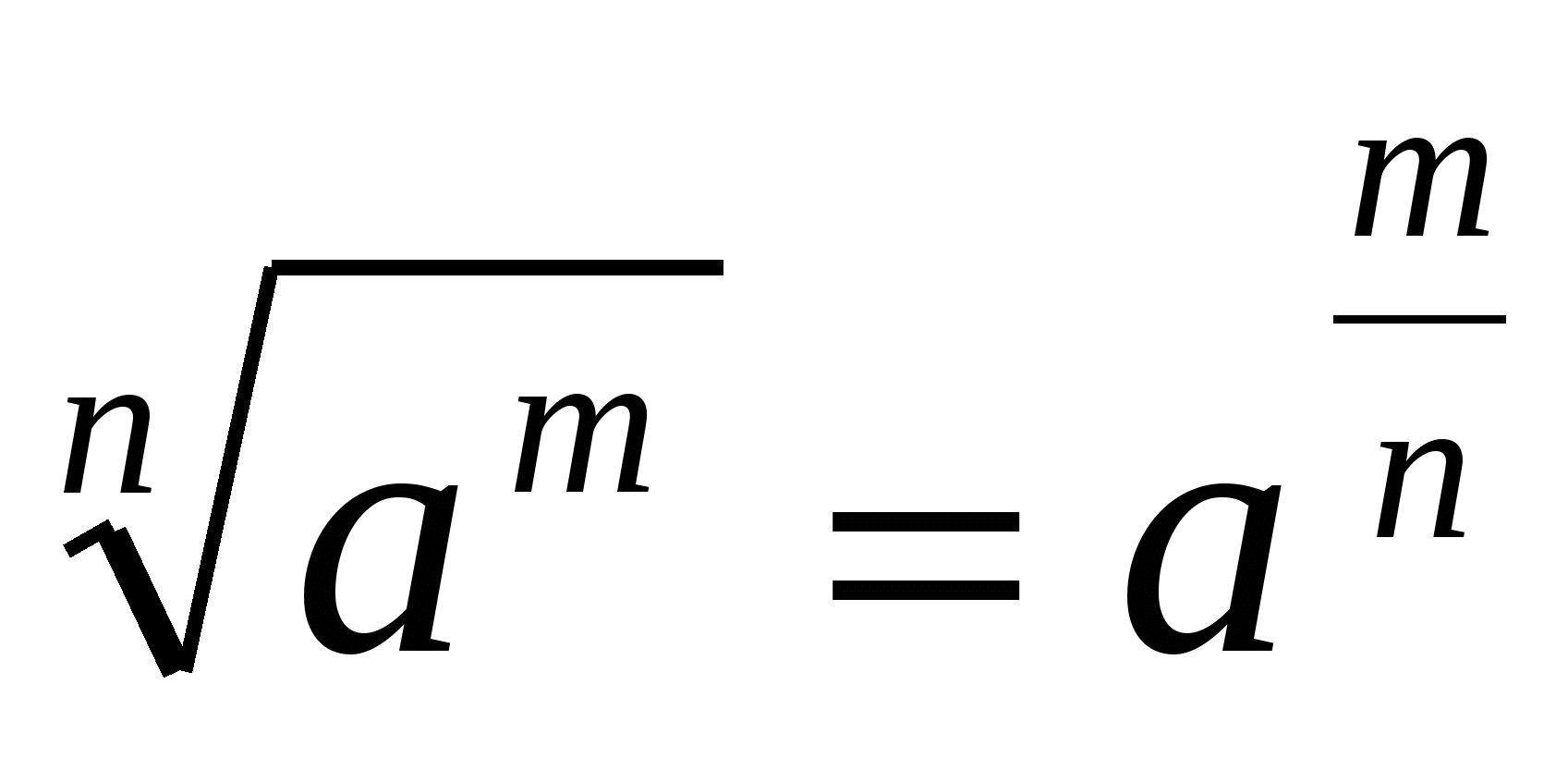
Любую степень с рациональным показателем можно представить в виде корня, чья степень будет равна знаменателю дроби, находящейся в показателе степени, а числитель будет степенью подкоренного выражения.

Свойства степени с рациональным показателем

Все, перечисленные ниже степени используются для рациональных чисел p, q и для положительных a, b.

1. Если Вам необходимо умножить две степени с рациональными показателями, которые имеют одинаковые основания, то в таком случае основание необходимо оставить без изменения, а показатели сложить.

a^p * a^q = a^p+q.

Например:

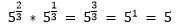
2. Если необходимо разделить две степени c рациональными показателями, которые имеют одинаковые основания, то в таком случае основание необходимо оставить без изменения, а показатели вычесть.

a^p / a^q = a^p-q .

Например,

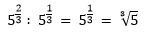
3. Если необходимо возвести одну степень в другую, основанием результата останется то же число, а показатели степени перемножаются.

(a^p )^q = a^p*q

Например,

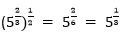
4. Если в некоторую степень необходимо возвести произведение произвольных чисел, то можно воспользоваться неким распределительным законом, при котором получим произведение различных оснований в одной и той же степени.

(a * b)^p = a^p * b^p

5. Аналогичное свойство можно применять для деления степеней, иначе говоря, для возведения обыкновенной двоби в степень.

(a / b)^p = a^p / b^q

6. Если некоторая дробь имеет отрицательный рациональный показатель степени, то для избавления от знака минуса, её следует перевернуть.

Например,

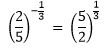
Корни

Любой корень - это иррациональное число. К иррациональным числам относятся корни, непериодические бесконечные дроби.

Квадратный корень - это неотрицательное число "а", подкоренное выражение которого равно данному числу "а" в квадрате.

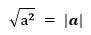
Например,

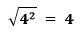
То есть в результате мы получим только положительное значение. Однако в качестве решения квадратного уравнения вида

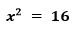
Решением будет х₁ = 4, х₂ = (-4).

Свойства квадратного корня

1. Какое бы значение не принимала величина x, данное выражение верно в любом случае:

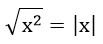
2. Сравнение чисел, содержащих квадратный корень. Чтобы сравнить данные числа, необходимо и одно, и второе число внести под знак корня. То число будет больше, чье подкоренное выражение больше.

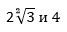
Вносим число 2 под знак корня

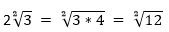
А теперь давайте внесем число 4 под знак корня. В результате этого получим

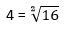
И только теперь два полученных выражения можно сравнить:

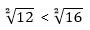
3. Вынесение множителя из под корня.

Если подкоренное выражение может разложиться на два множителя, один из которых можно вынести из под знака корня, то необходимо пользоваться данным правилом.

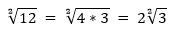
4. Существует свойство, обратное данному - внесение множителя под корень. Этим свойством мы заведомо воспользовались во втором свойстве:

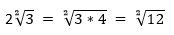
Корень степени n 1

Под корнем n-ой степени некоторого числа "a" понимают число, которое при возведении в степень "n" даст число "а".

Иными словами можно сказать, что это решение следующего уравнения:

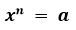
Например,

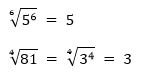
Если под корнем некоторой степени стоит степень, то для вынесения данного числа из под знака корня следует показатель степени разделить на степень корня.