Коррекционная карточка 8 класс:
Сокращение дробей (п.2).
Коррекционная карточка 8 класс:
Сложение и вычитание дробей с одинаковыми знаменателями (п.3).
Коррекционная карточка 8 класс:
Нахождение наименьшего общего знаменателя дробей (п.4).
Коррекционная карточка 8 класс:
Нахождение дополнительных множителей к дробям при приведении дробей к наименьшему общему знаменателю (п.4).
Коррекционная карточка 8 класс:
Приведение дробей к наименьшему общему знаменателю (п.4).
Коррекционная карточка 8 класс:
Сложение и вычитание дробей с разными знаменателями(п.4).
Коррекционная карточка 8 класс:
Умножение дробей (п.5).
Коррекционная карточка 8 класс:
Возведение в степень дроби (п.5).
Коррекционная карточка 8 класс:
Деление дробей (п.6).
Коррекционная карточка 8 класс:
Квадратный корень из произведения и частого. Произведение и частное корней (п.15).
Коррекционная карточка 8 класс:
Квадратный корень из степени(п.16).
Коррекционная карточка 8 класс:
Возведение квадратного корня в четную степень (п.11).
Коррекционная карточка 8 класс:
Решение уравнения х2=а (п.12).
|
Правило | Примеры |
| х2=−9 | х2=16 | х2−27=0 |
| Если а0, то х=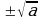 Если а=0, то х=0 Если а | −9 нет решений | х=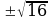 х = 4 | х2=27 х= 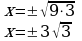
|
Коррекционная карточка 8 класс:
Вынесение множителя из-под знака корня (п.17).
| Правило | Примеры |
| 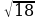
| 
| 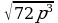
|
| 1. Разложить на множители подкоренное выражение так, чтобы были множители, из которых можно извлечь корень. | 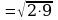
| 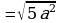
| 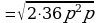
|
| 2. К получившемуся выражению применить свойство 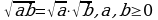 | 
| 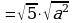
| 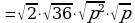
|
| 3. Вычислить значения корней или воспользоваться свойством 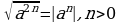
частный случай 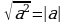
| 
| 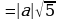
| 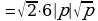
Так как p стоит под знаком корня p0 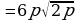
|
| Запись решения: | 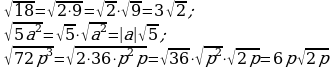
|
Коррекционная карточка 8 класс:
Внесение множителя под знак корня (п.17).
| Правило | Примеры |
| Удвоить показатель степени множителя и записать результат под знак корня. Если множитель отрицателен, поменять знак полученного выражения на противоположный. 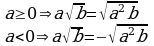
| 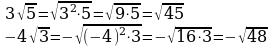
 , т.к. х стоит под знаком корня х , т.к. х стоит под знаком корня х
|
|
|
Коррекционная карточка 8 класс:
Преобразование выражений, содержащих корни (п.18).
| Правило | Примеры |
| Выяснить, какие тождественные и равносильные преобразования и в каком порядке нужно выполнить: 1 ) Раскрыть скобки (если нужно, применить формулы сокращенного умножения); 2) Вынести множитель из-под знака корня; 3) Использовать свойства корней; 4) Привести подобные слагаемые. 2. Поочередно выполнить все действия. | 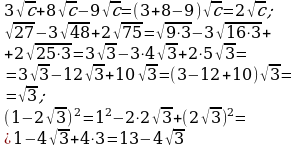
|
Коррекционная карточка 8 класс:
Разложение на множители выражений, содержащих корни (п.18).
| Правило | Примеры |
| 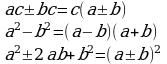
| 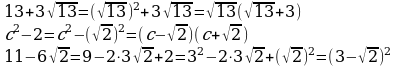
|
|
|
Коррекционная карточка 8 класс:
Сокращение дробей (п.18).
| Правило | Примеры |
| 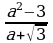
| 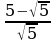
|
| 1. Разложить числитель и знаменатель на множители: вынести общий множитель за скобки; применить способ группировки слагаемых; применить формулы сокращенного умножения; использовать свойства степеней; другой способ. | 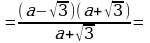
|  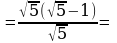
|
| 2. Зачеркнуть в числителе и знаменателе одинаковые множители в одинаковых степенях. |   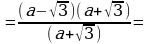
|  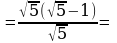
|
| 3. Записать в качестве ответа в числителе и знаменателе не зачеркнутые множители. | 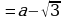
| 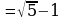
|
|
|
|
Коррекционная карточка 8 класс:
Освобождение от иррациональности в знаменателе (п.18).
| Примеры |
| 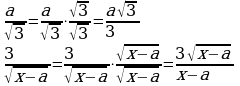 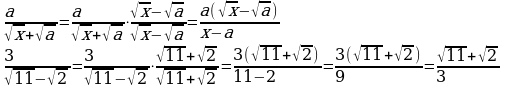
|
|
|
Коррекционная карточка 8 класс:
Решение неполных квадратных уравнений (п.19).
| Правило | Примеры |
| Уравнение вида: ах2=0 (a0) ах2=0 | : a х2=0 х=0 Ответ: х=0 | −6х2=0 | :(−6) x2=0 x=0 Ответ: х=0 |
| Уравнение вида: ах2+bx=0 (a0) ах2+bx=0 х(ax+b)=0 х=0 или ax+b=0 ax=−b | : a 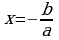 Ответ: х=0;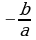 | 3х2−2х=0 х(3х−2)=0 х=0 или 3х−2=0 3х=2 | :3 х=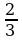 Ответ: х=0;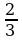 |
| Уравнение вида: ах2+c=0 (a0, c0) ах2+c=0 ах2=−c | :a х2= Если 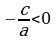 , то нет решений , то нет решений Если 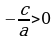 , то , то 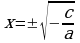 | 2х2+8=0 2х2=-8 | :2 х2=−4 −4 нет решений
Ответ: нет решений | −3х2+27=0 −3х2=−27 | :(−3) х2=9 х=3
Ответ: х=3
| 5(х−2)2-45=0 5(х−2)2=45 | :5 (х−2)2=9 x−2=3 x−2=−3 x=5 x= −1
Ответ: х= −1;5 |
Коррекционная карточка 8 класс:
Решение квадратных уравнений по формуле (п.21).
|
Правило | Примеры |
| –x(x+7)=(x–2)(x+2) | х2−6х+9=0 |
| 1. Определить, явл. ли уравнение уравнением вида 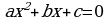 . Если «да», то п. 4, если «нет», то п. 2. . Если «да», то п. 4, если «нет», то п. 2. | нет | да |
| 2. Если нужно, раскрыть скобки; привести к общему знаменателю; поделить на число, не равное нулю; привести подобные слагаемые. | Раскрыть скобки, используя формулу разности квадратов. –x2–7x=x2–4 |
___________ |
| 3.Перенести все члены получившегося уравнения в левую часть уравнения меняя при этом знак на противоположный. Привести подобные слагаемые. Т.е. привести уравнение к виду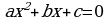 . . | –x2–7x– x2+4=0 –2x2–7x+4=0
|
__________ |
| 4. Выписать коэффициенты уравнения (a, b, c). | a= –2 b= –7 c=4 | a=1, b= −6, c=9 |
| 5. Вычислить дискриминант по формуле: D=b2-4ac | D= b2−4ac=(−7)2−4.(−2).4= =49+32=81 | D=b2−4ac= =(−6)2−4.1.9= =36−36=0
|
| 6. Если D Если D=0, то 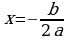 Если D0, то 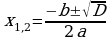 | D0 2 решения 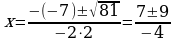
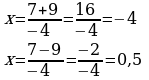
Ответ: x=-4; 0,5 | D=0 Один корень 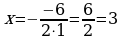
Ответ: х=3 |
Коррекционная карточка 8 класс:
Решение дробно-рациональных уравнений (п.24).
| Правило | Примеры |
| 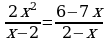
| 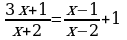
|
| 1. Найти наименьший общий знаменатель всех слагаемых, входящих в уравнение. | x – 2 | (x + 2)(x – 2) |
| 2. Найти область допустимых значений наименьшего общего знаменателя | ОДЗ: R\{2} | ОДЗ: R\{−2; 2} |
| 3. Умножить каждое слагаемое в уравнении на наименьший общий знаменатель. | 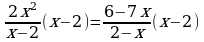
| 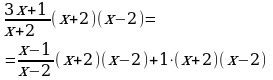
|
| 4. Упростить уравнение − сократить дроби − раскрыть скобки − перенести слагаемые − привести подобные слагаемые | 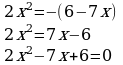
| 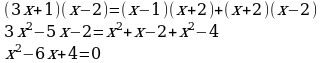
|
| 5. Решить получившееся уравнение | 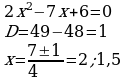
| 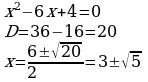
|
| 6. Проверить: входят ли полученные значения в область допустимых значений общего знаменателя | x =2 – не входит в ОДЗ | 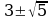 входят в ОДЗ входят в ОДЗ
|
| 7. Записать ответ. | 1,5 | 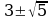
|







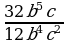
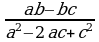
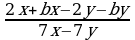
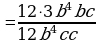
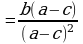
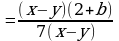


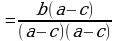
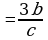

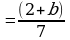
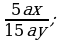 2)
2) 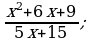 3)
3)  4)
4) 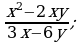 5)
5) 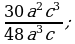 6)
6) 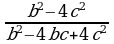
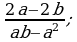 2)
2) 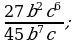 3)
3) 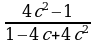 4)
4)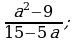 5)
5)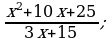 6)
6) 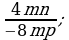
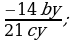 2)
2) 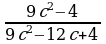 3)
3)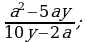 4)
4)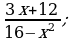 5)
5) 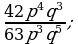 6)
6) 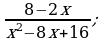
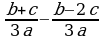
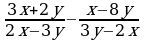
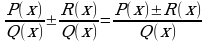

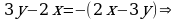
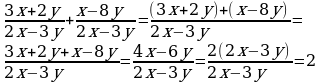
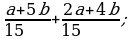 2)
2) 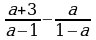 3)
3)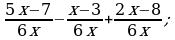 4)
4) 
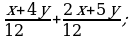 2)
2)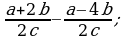 3)
3) 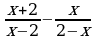 4)
4) 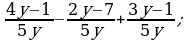
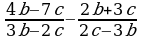 2)
2)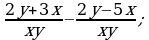 3)
3) 4)
4)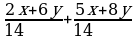
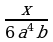 и
и 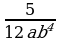
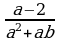 и
и 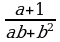
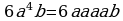 ;
; 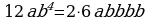
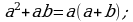
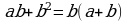
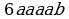 ;
; 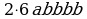

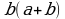
 =
=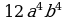
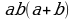
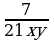 и
и  2)
2) 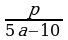 и
и 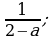 3)
3)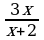 и
и 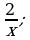 4)
4) 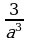 и
и 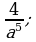 5)
5)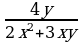 и
и 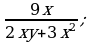
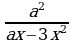 и
и 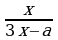 2)
2)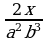 и
и 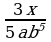 3)
3)  и
и 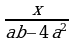 4)
4)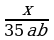 и
и 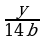
 и
и 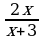
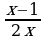 и
и 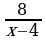 2)
2)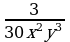 и
и 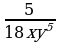 3)
3) 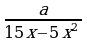 и
и 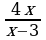 4)
4) 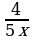 и
и 
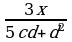 и
и 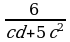

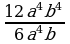


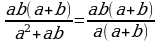
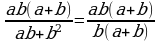
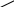
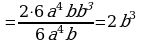
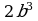 – дополнительный множитель к
– дополнительный множитель к 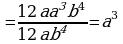
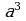 – дополнительный множитель к
– дополнительный множитель к 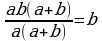
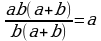
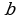 – дополнительный множитель к
– дополнительный множитель к 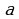 – дополнительный множитель к
– дополнительный множитель к 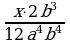
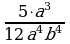
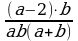
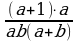
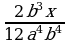 и
и 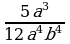
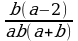 и
и 
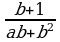
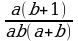
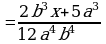



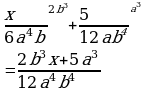
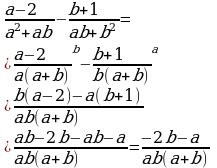
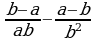 2)
2) 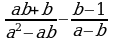 3)
3) 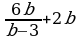 4)
4) 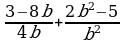 5)
5) 
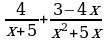 2)
2)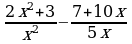 3)
3) 4)
4)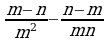 5)
5)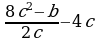
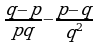 2)
2) 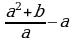 3)
3)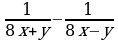 4)
4) 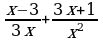 5)
5) 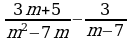
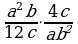
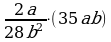
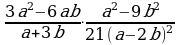

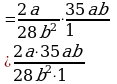
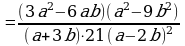
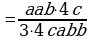
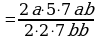

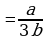
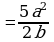
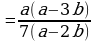
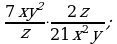 2)
2) 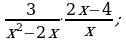 3)
3)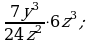 4)
4) 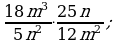 5)
5)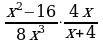
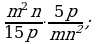 2)
2)  3)
3) 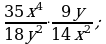 4)
4) 5)
5) 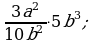
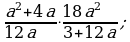 2)
2)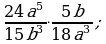 3)
3)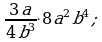 4)
4) 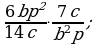 5)
5)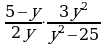
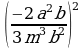
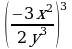
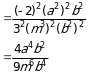
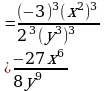
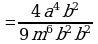
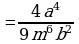
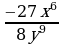
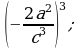 2)
2) 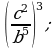 3)
3) 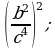 4)
4) 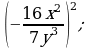 5)
5) 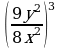
 2)
2)  3)
3) 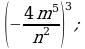 4)
4) 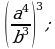 5)
5) 
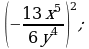 2)
2)  3)
3) 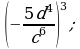 4)
4) 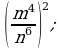 5)
5) 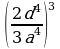
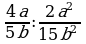
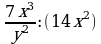
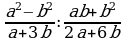
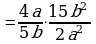
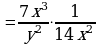

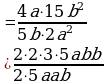
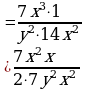
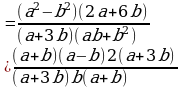
 2)
2)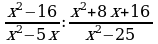 3)
3) 4)
4)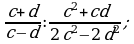
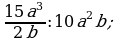
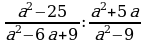 2)
2)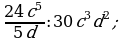 3)
3)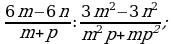 4)
4) 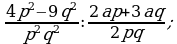
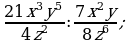
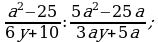 2)
2)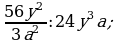 3)
3)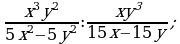 4)
4)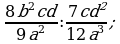
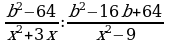
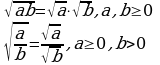
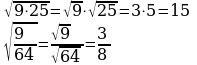
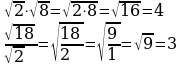
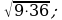 2)
2)  3)
3) 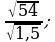 4)
4) 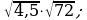 5)
5)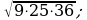
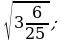 7)
7) 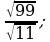 8)
8) 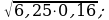 9)
9) 10)
10) 
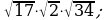 12)
12) 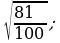 13)
13) 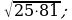 14)
14) 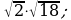 15)
15)
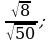 17)
17) 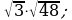 18)
18) 19)
19) 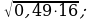 20)
20)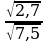
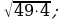 2)
2) 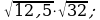 3)
3) 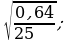 4)
4) 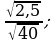 5)
5)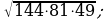
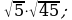 7)
7) 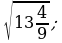 8)
8) 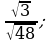 9)
9)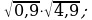 10)
10) 
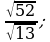 12)
12) 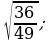 13)
13)  14)
14)  15)
15)
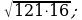 17)
17) 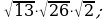 18)
18)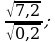 19)
19) 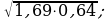 20)
20)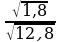
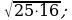 2)
2) 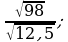 3)
3)  4)
4) 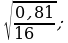 5)
5)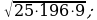
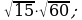 7)
7) 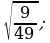 8)
8)  9)
9) 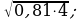 10)
10)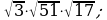
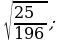 12)
12) 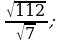 13)
13) 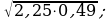 14)
14)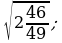 15)
15) 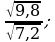
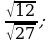 17)
17) 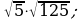 18)
18) 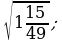 19)
19) 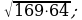 20)
20)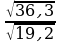
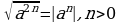
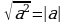
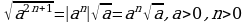
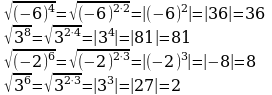
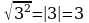

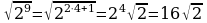
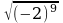 – не имеет смысла, т.к.–2 (–2)9
– не имеет смысла, т.к.–2 (–2)9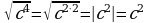 ,т.к с2 всегда положительно
,т.к с2 всегда положительно если x0, то
если x0, то 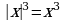
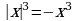
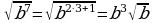
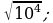 2)
2) 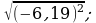 3)
3) 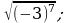 4)
4) 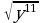 5)
5) 6)
6) 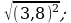 7)
7)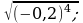 8)
8) 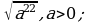
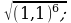 10)
10)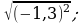 11)
11) 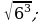 12)
12) 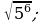 13)
13) 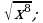 14)
14)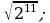 15)
15) 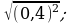 16)
16) 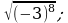
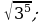 18)
18) 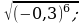 19)
19)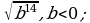 20)
20) 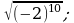
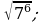 2)
2) 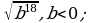 3)
3)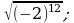 4)
4) 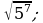 5)
5)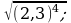 6)
6) 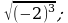 7)
7) 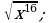 8)
8)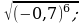
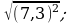 10)
10)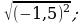 11)
11) 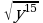 12)
12)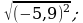 13)
13)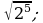 14)
14)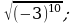 15)
15)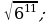 16)
16)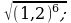
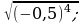 18)
18) 19)
19) 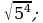 20)
20) 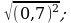
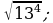 2)
2)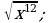 3)
3)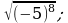 4)
4) 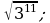 5)
5)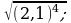 6)
6)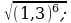 7)
7)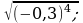 8)
8)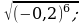
 10)
10)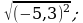 11)
11)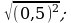 12)
12)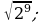 13)
13)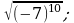 14)
14)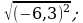 15)
15)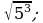
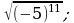 17)
17) 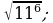 18)
18)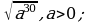 19)
19)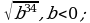 20)
20)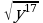
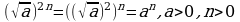 частный случай
частный случай 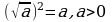
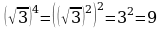
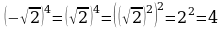
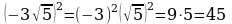
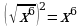
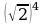 2)
2) 3)
3)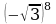 4)
4)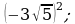 5)
5)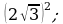 6)
6)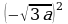 7)
7)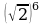 8)
8)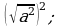 9)
9) 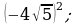
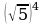 2)
2) 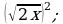 3)
3)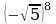 4)
4)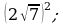 5)
5)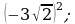 6)
6) 7)
7)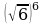 8)
8)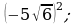 9)
9)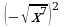
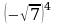 2)
2)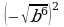 3)
3)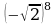 4)
4) 5)
5) 6)
6)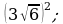 7)
7)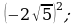 8)
8)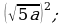 9)
9) 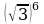
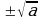
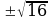

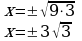
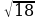

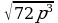
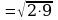
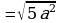
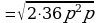
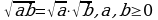
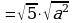
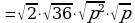

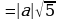
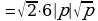
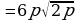
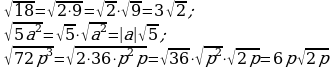
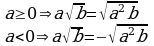
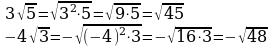
 , т.к. х стоит под знаком корня х
, т.к. х стоит под знаком корня х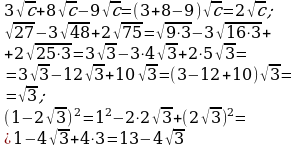
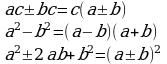
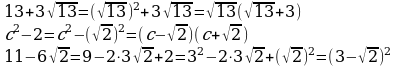
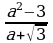
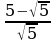
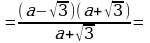

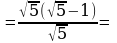
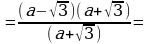
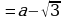
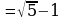
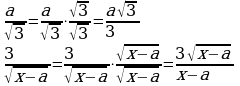
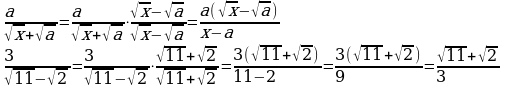
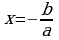
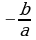
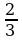

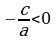 , то нет решений
, то нет решений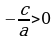 , то
, то 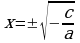
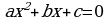 . Если «да», то п. 4, если «нет», то п. 2.
. Если «да», то п. 4, если «нет», то п. 2.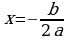
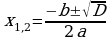
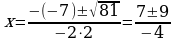
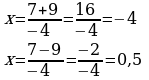
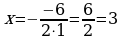
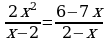
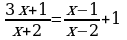
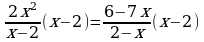
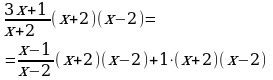
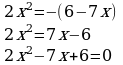
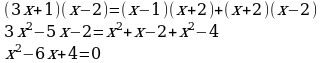
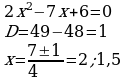
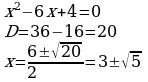
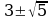 входят в ОДЗ
входят в ОДЗ



















