Управление образования администрации Тогучинского района Новосибирской области
Муниципальная научно-практическая конференция школьников
Секция: Математика
(название)
Беседина Анна Владимировна
(Ф.И.О. автора)
«Квадратичная функция в архитектуре и строительстве»
(тема работы)
МКОУ Тогучинского района «Тогучинская средняя школа № 4», 8 класс
(ОО, класс)
Руководитель
Ладошкина Надежда Сергеевна
Учёная степени нет
Квалификационная категория первая
Стаж работы 16
Место работы МКОУ Тогучинского района
«Тогучинская средняя школа № 4»
Должность учитель математики
2019-2020 гг
Содержание
| 1. Введение. | 3 |
| 2. История появления параболы. | 4 |
| 3. Определение функции и графика параболы. | 5 |
| 4. Квадратичная функция и архитектура. | 8 |
| 5. Архитектура и графики квадратичной функций. | 10 |
| 6. Задачи с использованием квадратичной функции | 11 |
| 7. Способы построения параболы | 16 |
| 8. Опрос | 17 |
| 9. Вывод | 18 |
| 10. Список использованной литературы | 18 |
| 11. Приложение | 19 |
Введение.
Каждый человек хоть раз, но видел дугообразные элементы в современной архитектуре, напоминающие радугу на небе. Посещая Новосибирск и другие города России, я обратила внимание, что есть современные построения, своей формой напоминающие график параболы. А если сильно быстро размешивать чай в стакане, то получается воронка, напоминающая параболу. Что это случайность или мы действительно можем встретить параболу в жизни и в сооружениях, созданных человеком. Мне стало интересно, как создаются элементы и чертежи таких зданий, сооружений и мостов и имеют ли они какое-то отношение к математике.
Считаю данную тему актуальной, т.к. в скором будущем мне необходимо будет сдавать экзамены и разобравшись с данной темой, мне удастся решить задачи связанные с квадратичной функцией.
Цель моей работы: определить есть ли элементы графика квадратичной функции в архитектуре
Определив цель своей работы, ставлю следующие задачи:
изучить литературу о параболе;
научиться строить график функции различных видов;
найти задачи, включающие в себя квадратичную функцию;
найти взаимосвязь между элементами зданий и параболой;
провести опрос и сделать выводы.
Методы и приемы исследования: наблюдение, моделирование на компьютере, поисковый метод, анализ и сравнение данных.
Объект исследования: график квадратичной функции, здания и сооружения.
Гипотеза: я считаю, что параболу можно встретить в строениях, созданных человеком и некоторые объекты, не только в строительстве, имеют форму параболы.
История появления параболы.
Математики Древней Греции открыли параболу еще в 260-170 гг. до нашей эры при изучении конических сечений.
По легенде которая дошла до нашего времени, Архимед построил вогнутые зеркала и с их помощью сжег римские корабли. (приложение 1) Но во время бурного развития оптики в XVII веке над этим утверждением стали смеяться, т.к., во-первых, линзы и зеркала с заданными поверхностями для оптики стали делать только с конца XVI века (и греки не знали свойств этих устройств), а во-вторых, даже если бы знали, то изготовление таких устройств размером больше метра требовало технологий, которых у древних греков просто не было.
Действительно, греки не умели изготавливать метровые оптические приборы, но это не означало, что Архимед не мог поджечь римские корабли. Греческий исследователь Ионис Саккас в 1973 году придумал и осуществил изящный эксперимент, возможно, повторивший историческое событие. У защитников Сиракуз точно были плоские бронзовые щиты. А если направить отраженный свет от этих щитов в одно место, фактически совместив много больших солнечных зайчиков? Сколько таких щитов нужно? Саккас оценил, что необходимо от 30 до 100 щитов размером от одного до двух квадратных метров каждый и провел эксперимент.
50 человек для чистоты эксперимента взяли частично поцарапанные и загрязненные плоские бронзовые листы размером метр на полтора и направили солнечные «зайчики» от них на макет римской триеры, расположенной в сорока метрах от них. Время эксперимента и день выбрали так, чтобы поток солнечных лучей был средним, а не максимальным. Несмотря на это, не прошло и двух минут, как под возгласы удивленной публики макет триеры загорелся. Саккас считает, что при более сильном солнце и большем числе «щитов» лодка могла бы загореться и буквально за несколько секунд, а значит, таким образом можно было бы быстро сжечь несколько рядом стоящих кораблей. Получается, что легенда об Архимеде скорее всего — быль, и не требует хитроумных и больших зеркал.
Итог, полученный Архимедом, основан на следующем утверждении: любая прямая, параллельная оси симметрии параболы, после отражения от параболы проходит через ее фокус.
Уже в 17 веке Галилео Галилей доказал, что тело, брошенное под углом к горизонту, двигается по параболе. (приложение 2) Параболу мы наблюдаем в жизни, как траекторию движения какого-либо тела. В баскетболе, брошенный мяч в корзину, летит по параболе (приложение 3). Струя фонтана, «вычерчивает» линию, которая очень схожа с параболой (приложение 4).
Определение функции и графика параболы.
Понятие функции уходит своими корнями в ту далёкую эпоху, когда люди впервые поняли, что окружающие их предметы взаимосвязаны. Они ещё не умели считать, но уже знали, что чем больше оленей удастся убить на охоте, тем дольше племя не будет голодать. В Древнем Вавилоне были составлены таблицы для функций у=х², у=х³, у=х²+х³. Понятие переменной величины было введено в науку французским учёным и математиком Рене Декартом (1596-1650г.г.) (приложение 5). Он ввёл идею числовой функции числового аргумента. При записи зависимостей между величинами Декарт стал применять буквы. Он начал геометрически изображать не только пары чисел, но и уравнения, связывающие два числа.
С квадратичной функцией мы уже имели дело при работе с некоторыми формулами на уроках математики в 6 классе. Например, формула S=πr² задаёт площадь круга как квадратичную функцию его радиуса r. Формула S=a² задаёт площадь квадрата как квадратичную функцию его стороны. А в 8 классе мы начали изучать квадратичную функцию y=ax2. Графиком данной функции является парабола. Мне стало интересно, для чего мы её изучаем, и где её можно увидеть. Я решила найти информацию в энциклопедии и открыла для себя много интересного. Оказалось, что парабола окружает нас повсюду. Начнём с простого. Параболическая антенна, ее можно увидеть около любого аэродрома (приложение 6). Используется для того, чтобы собрать в одну точку сигналы радиолокатора, отраженные от самолета. В прожекторах свет, исходящий из фокуса параболического зеркала, после отражения образует параллельный пучок и не рассеивается (приложение 7). Поэтому автомобильные фары имеют форму параболоида.
Анализируя полученную информацию я решила поделится ею и написать исследовательскую работу. И начала я с классического определения парабола.
Пара́бола (греч. παραβολή — приложение) — геометрическое место точек, равноудалённых от данной прямой (называемой директрисой параболы) и данной точки (называемой фокусом параболы) (приложение 8 ). Вершина данной параболы находится в точке (0;0), основные свойства функции : 1) D(f) R, 2) E(f) R+; 3) функция имеет ось симметрии – ось ординат.
Квадратичная функция — целая рациональная функция второй степени вида, F(x)=ax2+bx+c, где x переменная и a, b, c – коэффициенты квадратичной функции.
Коэффициент - это числовой множитель, в общем виде коэффициенты обозначаются маленькими латинскими буквами, у параболы существуют 3 коэффициента, a, b и c, каждый из них определяет расположение параболы в системе координат.
а – старший коэффициент, определяет направление ветвей параболы, их сжатие/растяжение вдоль оси oy
b – второй коэффициент, показывает сдвиг вершины по оси ОХ
с - свободный член, это координата пересечения параболы с осью ординат
Рассмотрим на примере нескольких функций: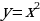 ,
, 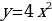 ,
,  ,
, 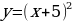 ,
, 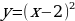
Первая пара функций, которые я рассмотрела - это y = x2 и y = 4x2. Для построения функций, использовала таблицы значений. Ветви данных парабол направлены вверх, т.к. старший коэффициент 0. Из таблиц видно (приложение 9 ), что при одних и тех же значениях аргумента значения функции у = 4x2 графика больше в 4 раза. Графически это означает, что график функции 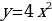 сужается по сравнению с графиком функции
сужается по сравнению с графиком функции 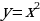 (приложение 10 ).
(приложение 10 ).
Если необходимо построить график функций  , то из таблиц видно (приложение 11 ), что при одних и тех же значениях аргумента значения функции у графика
, то из таблиц видно (приложение 11 ), что при одних и тех же значениях аргумента значения функции у графика  меньше в 5 раз, чем у
меньше в 5 раз, чем у 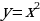 . Графически это означает, что график функции
. Графически это означает, что график функции  расширяется по сравнению с графиком функции
расширяется по сравнению с графиком функции 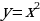 , ветви парабол направлены вверх (приложение 12 ).
, ветви парабол направлены вверх (приложение 12 ).
Следующую пару функций, которые я рассматривала, это функции y = x2 и y = (x + 5)2. Из таблиц видно (приложение 13), что одинаковым значениям функции соответствуют значения аргумента, отличающиеся на 5 единиц. Это означает, что график данной функции переместился на 5 единиц относительно оси ординат влево (приложение 14), так как для получения одинаковых значений функций приходится брать значения аргумента на 5 меньше:
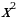 =0, при x=0
=0, при x=0
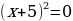 при x=-5
при x=-5
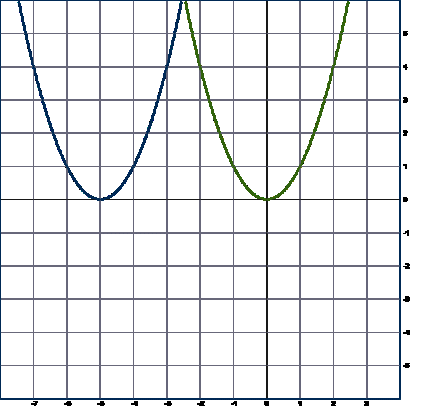
Следовательно, если необходимо было построить график функции 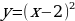 , то сдвиг на 2 единицы относительно оси ординат был бы вправо (по сравнению с графиком функции
, то сдвиг на 2 единицы относительно оси ординат был бы вправо (по сравнению с графиком функции 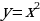 ) (приложение 15 ).
) (приложение 15 ).
Следующие функции, которые я исследовала, это функции y = x2 и y = x2 + 7 и y = x2 - 3
Из таблиц видно (приложение 16), что значения функции y = x2 + 7 отличаются от значений функции y = x2 на 7 единиц, т.е. график функции y = x2 + 7 смещается по оси oy вверх, а график функции y = x2 – 3 смещается вниз на 3 единицы.
Следующую функцию, которую я исследовала, эта функция была представлена квадратичной функцией полного вида y = ax2 + bx + c. Я рассмотрела функцию y = 3x2 - 3x + 4. Ветви параболы направлены вверх, т.к. старший коэффициент а = 3, 3 0. Для того, чтобы построить график данной функции, определила сначала координаты вершины параболы. Воспользовалась формулой: xв = 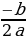 , xв =
, xв = 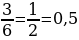 , yв = 3 * 0,52 – 3 * 0,5 + 4 = 3,25. Получилась координата вершины параболы (0,5; 3,25). Затем использовала для построения параболы таблицу и построила график функции по точкам (приложение 17).
, yв = 3 * 0,52 – 3 * 0,5 + 4 = 3,25. Получилась координата вершины параболы (0,5; 3,25). Затем использовала для построения параболы таблицу и построила график функции по точкам (приложение 17).
Квадратичная функция и архитектура.
Квадратичная функция является самой популярной функцией, как в математике, так и в архитектуре.
В современном понимании архитектура — это искусство проектировать и строить здания, сооружения и их комплексы.
Сложность этого процесса заключается в необходимости создания архитектурных объектов, которые сочетают в себе высокое качество строительства и функциональность предлагаемых помещений.
В основах множества строений часто встречается парабола, ветви которой идут по направлению вниз.
Симметричность же данной функции относительно оси абсцисс позволяет достигать равномерного распределения нагрузки, что способствует устойчивости и прочности сооружений, в основе которых так или иначе она применяется.
Строения такого вида очень привлекательны. Большинство мостов и арок по всему миру построены именно таким образом.
В применении параболической дуги при постройке мостов и кровельных перекрытий можно различать не менее четырех различных типов.
Первый тип представляют висячие мосты с тросами, провисающими по кривой параболической формы (приложение 18).
Ко второму типу, относится вершина параболической арки, находится под проезжей частью (приложение 19).
Третий тип, параболическая арка пересекает проезжую часть (приложение 20).
Сооружения, у которых параболическая арка целиком расположена над путем, как в случае перекрытий, принадлежат к четвертому типу (приложение 21).
В России множество подобных строений, рассмотрим некоторые из них:
Филиал Казанского (Приволжского) федерального университета в г. Елабуга (приложение 22) .
Крестовоздвиженская церковь Казанско-Богородицкого монастыря в г. Казань (приложение 23). Купола этих архитектурных сооружений являются конструкциями параболической формы. Плавность и в тоже время четкость изгибов параболической функции, лежащей в основе куполов, позволяет им гармонично вписываться во внешний облик здания, не утяжеляя его.
Арка влюбленных в Парке Черное озеро в г. Казань (приложение 24). Благодаря особенностям конструкции арка обладает удивительным акустическим эффектом. Двое влюбленных, находящихся по разные стороны арки, могут шепотом признаваться друг другу в любви, и каждое слово будет услышано любимым человеком.
Лебедевский (Горбатый) мост, г. Казань (приложение 25).
Тогучинский мост (приложение 26).
Бугринский мост (приложение 27).
Архитектура и графики квадратичной функции
Мне стало интересно сравнить элементы мостов и графики функции в изображение, можно увидеть это в данной таблице
|

балхейвенский мост | 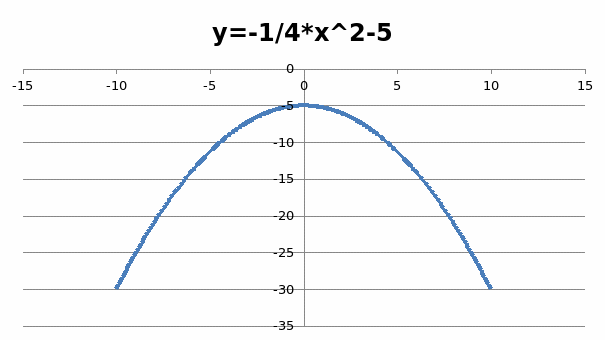
|
| 
Бычихинский мост | 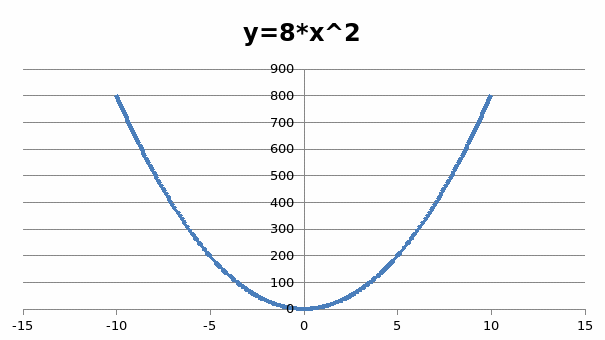
|
|

грантс пасс мост | 
|
| 
Мост в Пскове | 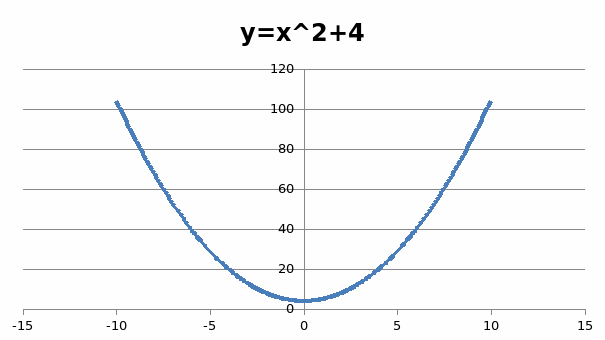
|
| 
Тогучинский мост | 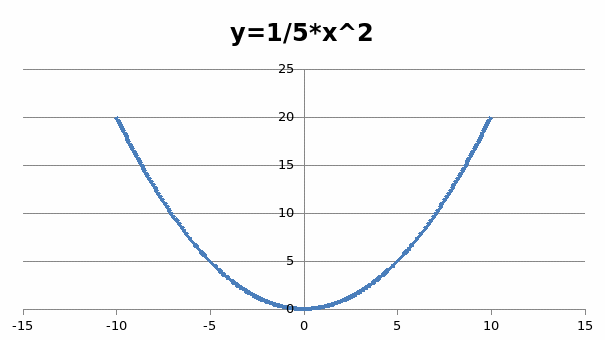
|
Задачи с использованием квадратичной функции
Работая над данной темой, я рассмотрела много различных задач, где используется квадратичная функция. Приведу некоторые из них.
Задача 1. Найти нули квадратичной функции y = x2 – 4. Чтобы найти координаты точек нулей функции, нужно в исходную функцию подставить вместо «y» число нуль.
Решение: х2 -4 = 0
х2 = 4
х1 = 2; х2 = -2
Ответ: нули функции (2;0) и (-2;0)
Задача 2. Определить, при каких значениях х, квадратичная функция y = 2x2 – x – 6, принимает заданное числовое значение -6. Чтобы найти значение х, необходимо вместо y подставить числовое значение -6 и решить полученное квадратное уравнение, относительно переменной х.
Решение: 2х2 – х – 6 = - 6 2х2 - х = 0
2х2 – х = -6 + 6 х(2х – 1) = 0
х = 0 или 2х -1 = 0
х = 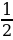
Ответ: при х = 0 и х = 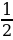 функция y = 2x2 – x – 6, принимает значение -6.
функция y = 2x2 – x – 6, принимает значение -6.
Задача 3. Определить координаты точек пересечения квадратичной функции и линейной функции. Функции заданы формулами y = x2 – 3x – 7 и y = -6x – 3. Чтобы найти координаты точек пересечения данных функций необходимо: 1) приравнять правые части функций (те части функций, которые содержат переменную «х»); 2) решить полученное уравнение относительно переменной х; 3) полученные значения переменной х, подставить в любую из функций, чтобы получить значение переменной y.
Решение: x2 -3x – 7 = -6x – 3
x2 – 3x + 6x – 7 + 3 = 0
x2 + 3x – 4 = 0, a = 1, b = 3, c = - 4
Вычислим дискриминант, по формуле D = b2 - 4*a*c, D = 32 – 4*1*(-4) = 25, D0, значит функция имеет 2 корня. Найдем корни уравнения по формуле 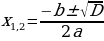 .
. 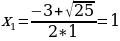 ,
, 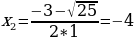 . Подставим в функцию y = -6x – 3 и найдем значения функции. у1 = -6 * 1 - 3 = - 9, у2 = - 6 * (- 4) – 3 = 21. Получили две точки пересечения параболы и прямой.
. Подставим в функцию y = -6x – 3 и найдем значения функции. у1 = -6 * 1 - 3 = - 9, у2 = - 6 * (- 4) – 3 = 21. Получили две точки пересечения параболы и прямой.
Ответ: координаты точек пересечения (1; -9) и (-4; 21)
Задача 4. Определить, принадлежит ли точка с координатами (-4; 7), графику функции y = -2x2 – 4x + 9. Чтобы определить принадлежит ли точка графику функции, необходимо подставить координаты точки в функцию и если получится верное равенство, то точка принадлежит графику функции.
Решение: Подставим в y = -2x2 – 4x + 9 координаты. 7 = -2 * (-4)2 – 4 * (-4) + 9. Получим: 7 = -7. Вывод: точка не принадлежит графику функции y = -2x2 – 4x – 9
Задача 5. Определить при каких значениях х функция принимает положительные или отрицательные значения.
Ч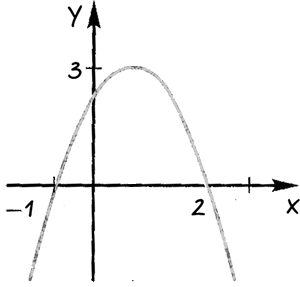 тобы по графику функции определить, где функция принимает положительные или отрицательные значения нужно:
тобы по графику функции определить, где функция принимает положительные или отрицательные значения нужно:
провести прямые через точки в местах, где график пересекает ось «Ox»;
определить положительные или отрицательные значения принимает функция на промежутках между проведенными прямыми;
записать ответ для каждого промежутка относительно «x».
Р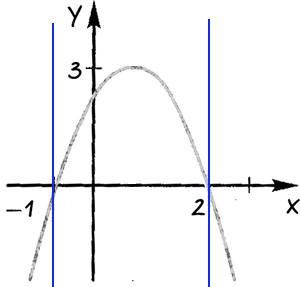 ассмотрим пример, задан график функции, по графику определить при каких значениях х, функция принимает положительные и отрицательные значения.
ассмотрим пример, задан график функции, по графику определить при каких значениях х, функция принимает положительные и отрицательные значения.
Проведем через точки, где график функции пересекает ось «Ox» прямые.
О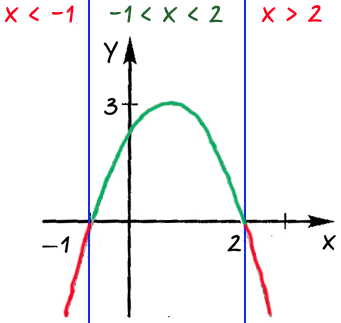 пределим области, где функция принимает отрицательные или положительные значения.
пределим области, где функция принимает отрицательные или положительные значения.
П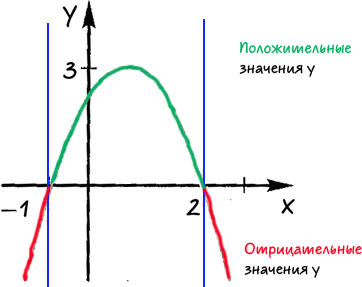 одпишем над каждой полученной областью, какие значения принимает «x» в каждой из выделенных областей.
одпишем над каждой полученной областью, какие значения принимает «x» в каждой из выделенных областей.
Ответ: при «x » и «x 2» функция принимает отрицательные значения; при «−1 » функция принимает положительные значения.
Задача 6. Парабола проходит через точки K(0; –5), L(3; 10), M( –3; –2). Найдите координаты её вершины.
Решение: Для того чтобы найти координаты вершины параболы, нужно знать формулу, которая задает квадратичную функцию. Для этого необходимо найти коэффициенты a, b, c. А для того, чтобы их найти необходимо подставить координаты точек, через которые проходит парабола и решить систему.
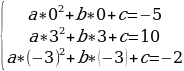
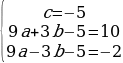
Сложим второе и третье уравнение, получим: 18a - 10 = 8. Решим получившееся уравнение, получим 18a = 18, a = 1. Подставим 9*1 + 3b – 5 = 10, 3b = 6, b = 2. Значит 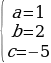 , составим формулу заданной квадратичной функции: y = x2 + 2x -5. Найдем для данной функции, координаты вершины, воспользуемся формулой
, составим формулу заданной квадратичной функции: y = x2 + 2x -5. Найдем для данной функции, координаты вершины, воспользуемся формулой 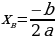 .
. 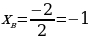 , yв = (-1)2 + 2*(-1) -5 = -6.
, yв = (-1)2 + 2*(-1) -5 = -6.
Ответ: Координаты вершины квадратичной функции (-1; -6)
В жизни встречаются такие задачи, решение которых напрямую связаны с квадратичной функцией, либо с формулой, либо с графиком. Вот некоторые из них:
1) Шуточная задача: Когда Таня перестанет плакать?
Наша Таня громко плачет
Уронила в бассейн мячик
Тише, Танечка, не плачь,
Включим воду, всплывет мяч
Математическое условие: После открытия крана в бассейн начинает поступать вода, при этом высота столба, выраженная в метрах, меняется по закону Н(t)=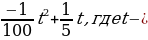 время, в минутах. Через какое время заполниться бассейн?
время, в минутах. Через какое время заполниться бассейн?
Решение. Построим параболу со следующими данными (приложение 28)
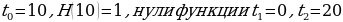 и учитывая жизненные условия, получим, что Таня перестанет плакать через 10 мин.
и учитывая жизненные условия, получим, что Таня перестанет плакать через 10 мин.
2) Один из способов измерения глубины пещер, колодцев, шахт и т.д. заключается в следующем: сверху сбрасывают камень и с максимально возможной точностью засекают время, через которое будет услышан звук от его удара о землю. Заполнить необходимо таблицу, если закон свободно падающего тела вычисляется по формуле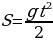 , g≈10 м/с2 (9,8 м/с2)
, g≈10 м/с2 (9,8 м/с2)
| h, м | 5 | 20 | 15 | 250 |
| t, с | 1 | 4 | 3 | 50 |
Решение: h = 5 t
2 t
2=
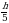
=
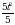
; то 1c
t2=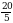 =4, то 2с и т.д.
=4, то 2с и т.д.
Эти данные помогают определить глубину объекта с подручными средствами, без всяких приборов.
3) Брандспойт, закреплённый под определённым углом на пожарной машине, выстреливает струю воды с постоянной начальной скоростью. Высота струи воды описывается формулой у = ах2 + bх + с, где а =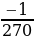 , b =
, b =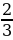 , с =
, с =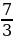 постоянные параметры. На каком максимальном расстоянии в метрах от забора нужно поставить машину, чтобы вода перелетала через верх? (приложение 29)
постоянные параметры. На каком максимальном расстоянии в метрах от забора нужно поставить машину, чтобы вода перелетала через верх? (приложение 29)
Высота забора равна 19 м.
Р е ш е н и е: траектория струи – парабола, ветви вниз, т. к. струя перелетает забор данной высоты, то прямая, проходящая через точку (0; 19),имеет две общие точки с параболой,
которые являются корнями трёхчлена.
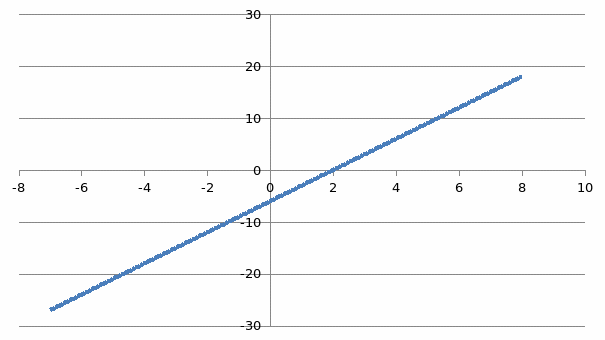
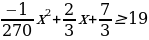 ,
,
– х2 + 180х + 630 ≥ 5130,
х2 – 180х + 4500 ≤ 0,
(х – 30)(х – 150) ≤ 0
30 ≤ х ≤ 150.
Наибольшее расстояние равно 150 метров.
О т в е т: 150 м.
Способы построения
Работая над данной темой, я рассмотрела несколько способов построения графика. На уроках математики рассматривается единственный способ построения параболы, а я нашла еще четыре способа.
1) Возьмем прямоугольный лист бумаги и отметим около его большой стороны точку N. Сложим лист так, чтобы точка N совместилась с какой-нибудь точкой M на большой стороне, и на бумаге образовалась линия сгиба h. Линия сгиба будет серединным перпендикуляром к отрезку MN и, следовательно, касательной к параболе. Разогнем лист и снова согнем его, совместив точку N с другой точкой большой стороны. Сделаем так несколько раз, пока вся бумага не покроется линиями сгибов. Линии сгибов будут касательными к параболе. Граница участка внутри этих сгибов будет иметь форму параболы (приложение 30)
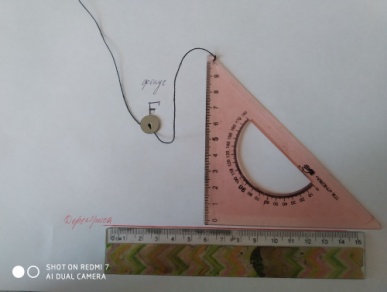
2) На листе бумаги нужно закрепить линейку (ее край будет директрисой будущей параболы), в точке, которая станет фокусом параболы, булавкой или кнопкой прикрепить конец нити, другой конец которой закрепить в вершине острого угла чертежного треугольника, притом так, чтобы длина нити равнялась катету этого треугольника. Перемещая второй катет вдоль линейки и, прижимая нить острием карандаша к первому катету треугольника, мы получим кривую, точки которой находятся на одинаковых расстояниях от края линейки и от точки, т.е. параболу (приложение 31). Оказывается, что парабола график квадратичной функции — обладает интересным свойством: есть такая точка и такая прямая, что каждая точка параболы одинаково удалена от этой точки и от этой прямой (точку называют фокусом параболы, а прямую — ее директрисой).
3) Способ третий такой: Построим прямую D, возьмем две точки: А принадлежащую прямой и В не принадлежащую прямой. Соединим эти точки взаимно перпендикулярными прямыми, точку пересечения назовем С. Отрезки АС и ВС делим на равное количество отрезков. Из точек на АС проводим параллельные прямые отрезка AD. Из точки А проводим прямые к каждой из точек на стороне СВ. в точках пересечения прямых последовательно, ставим точки, соеденеям их и получаем ветвь параболы (приложение 32).
4) Следующий способ построения параболы с использованием острого угла. Рассмотрим угол с вершиной О и сторонами n и m. На сторонах угла, отметим две фиксированные точки N0 и M0 соответственно, равноудаленные от вершины угла О. На сторонах n и m рассмотрим соответствующие последовательности точек N1, N2, N3, … и M1, M2, M3, …, при чем M0 M1 = N0 N1 и точки M1 и N1 расположены по разные стороны от прямой M0- N0
Перегибая угол по прямым M1N1 и разгибая, получим следы сгибов. Рассмотренное семейство прямых имеет огибающую, являющуюся параболой (приложение 33)
Опрос
Я решила провести опрос среди учащихся 7-8 классов, чтобы узнать, знают ли учащиеся моей школы о квадратичной функции, ее графике и можно ли встретить график параболы в жизни. Были заданы следующие вопросы:
вопрос 1: Выберете график квадратичной функции?
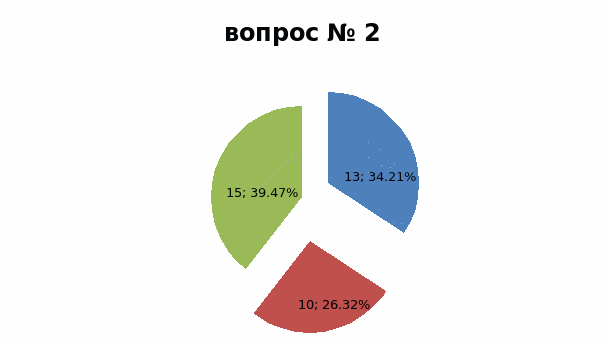
Вопрос 2: Кто был одним из первых ученных изучающих квадратичную функцию?
1) Пифагор 2) Фалес 3) Архимед
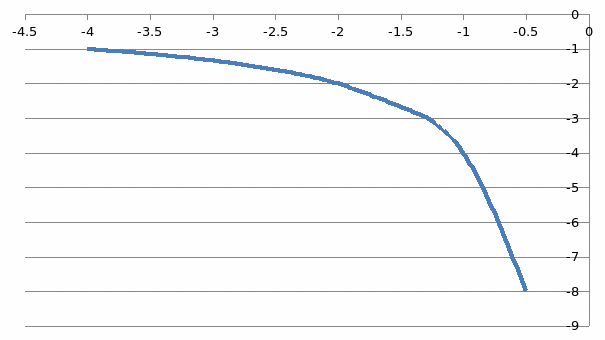
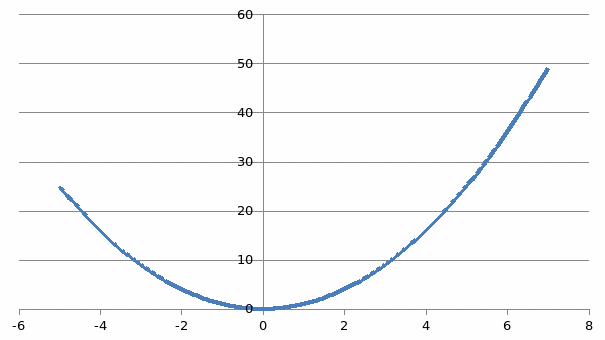
Вопрос 3: Выберите архитектурные сооружения, где можно встретить элементы, похожие на квадратичную функцию?
1) 2)
2)  3)
3) 
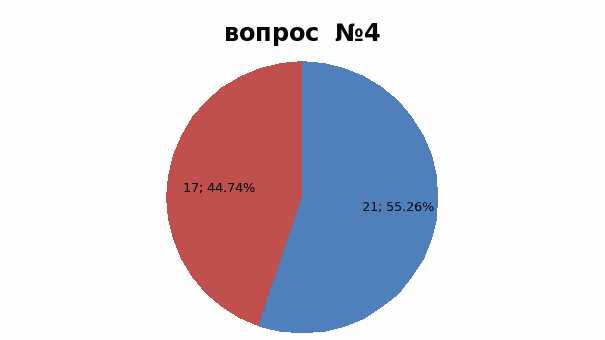
Вопрос 4: Имеет ли квадратичная функция свойство расширяться или сужаться?
1)да 2)нет
Результаты опроса представлены на диаграммах (приложении 34). Проанализировав результаты, можно сделать следующие выводы:
1) Третья часть опрошенных (37%) знают, как выглядит график квадратичной функции, т.к. изучали на уроках математики; 2) Около половины опрошенных (40%) верно отметили первого из ученых, открывших параболу. Учащиеся мало интересуются историей на уроках математики; 3) Ни один из учащихся, не выбрал оба правильных ответа, но 1 вариант выбрали 21%, а 2 - 47%; 4) Больше половины опрошенных (55%) выбрало верный ответ, что график квадратичной функции может сужаться и расширяться.
Выводы
По проделанной работе можно сделать следующие выводы: 1) человеком много создано сооружений, в которых встречается парабола. Да и не только здания и мосты имеют форму параболы, как оказалось много предметов в жизни окружают нас с такой формой. Так что гипотеза моя подтвердилась; 2) решение задач, которые я рассмотрела, мне пригодятся и на уроках математики, и при сдачи экзамена; Интересно было работать над не стандартными задачами, которые неожиданно стали связаны с математикой, а тем более с квадратичной функцией; 3) интересно было узнать новые способы построения параболы. Возникали трудности в построении, особенно когда необходимо использовать одновременно два или три инструмента. Думаю самый простой и более точный способ построения параболы, это по точкам.
Список использованной литературы
1. u.m.wikipedia.org
2. math-prosto.ru
3. infourok.ru
4. ege-ok.ru
5. interneturok.ru
ПРИЛОЖЕНИЯ
| Приложение 1

Архимед | П риложение 2 риложение 2
Галилео Галилей |
| П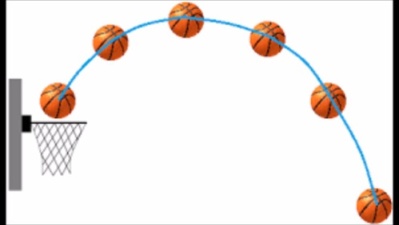 риложение 3 риложение 3
Траектория мяча
| Приложение 4
Ф онтан онтан |
| П риложение 5 риложение 5
Рене Декарт
| П риложения 6 риложения 6
Параболическая антенна |
| Приложения 7
Фара автомобиля 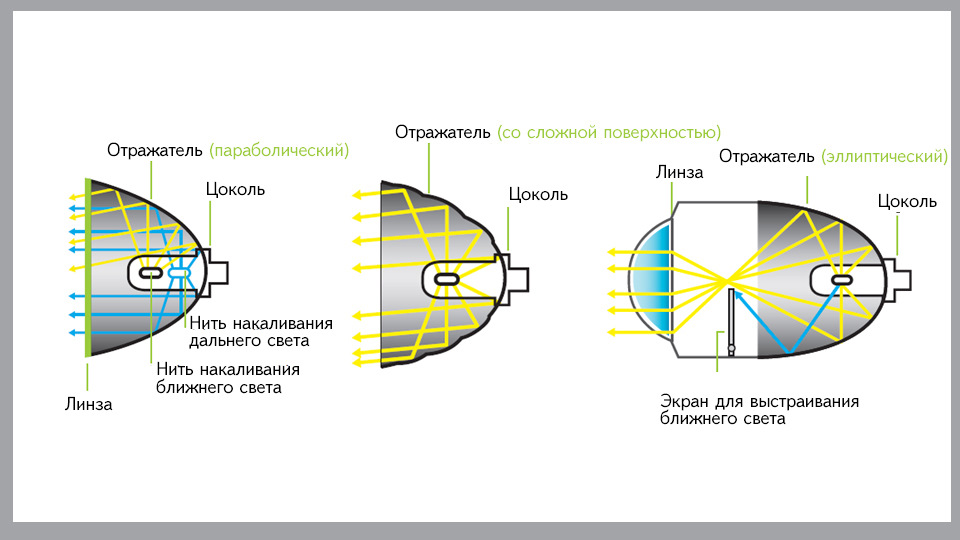  | Приложение 8 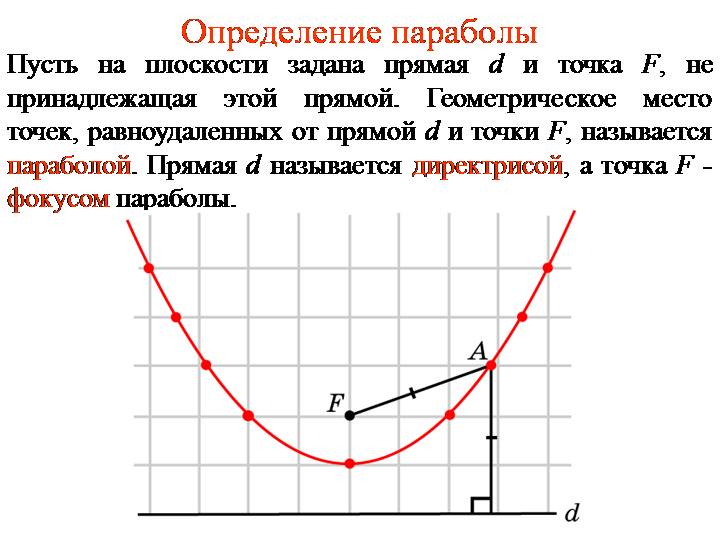
F-фокус параболы d- директриса
Парабола
|
| Приложение 9 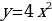
| x | 0 | -1 | 1 | -2 | 2 | -3 | 3 | | y | 0 | 4 | 4 | 16 | 16 | 36 | 36 |
y = x2
| x | 0 | -1 | 1 | -2 | 2 | -3 | 3 | | y | 0 | 1 | 1 | 4 | 4 | 9 | 9 |
| Приложение 10 Построение 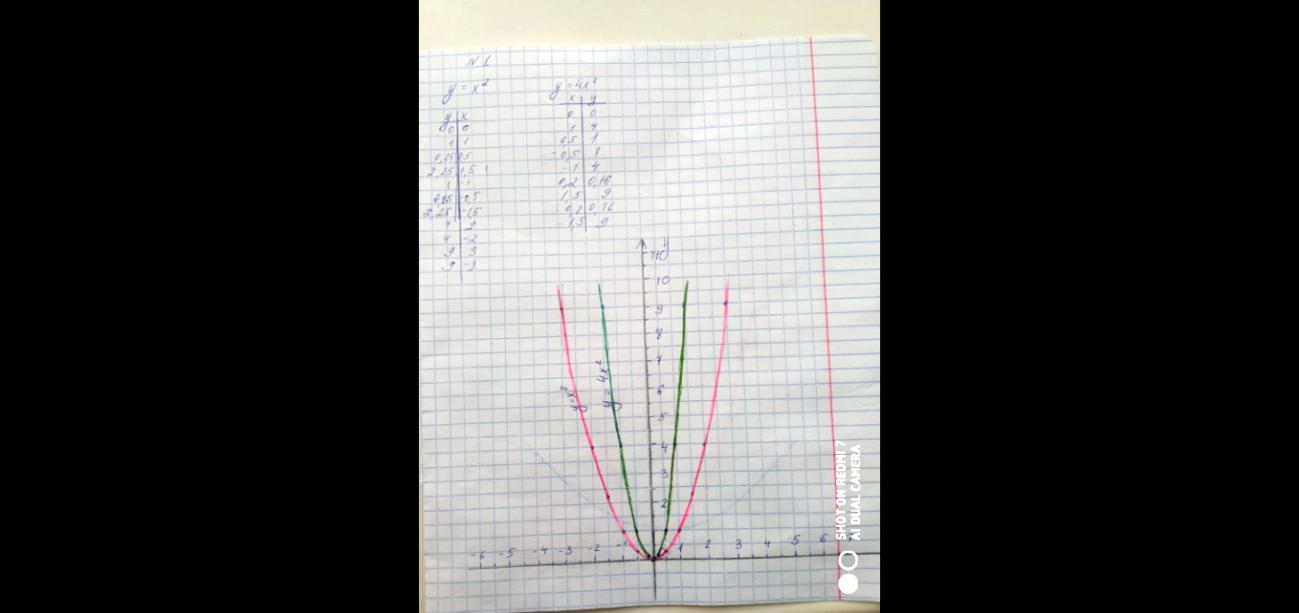
н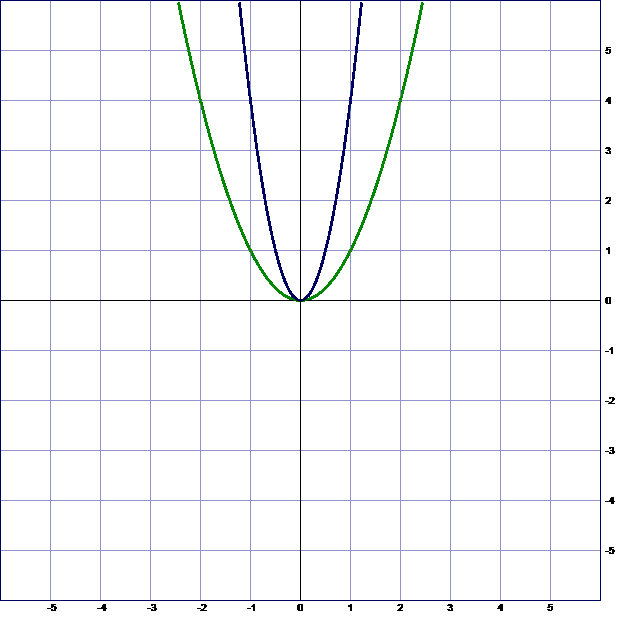 а компьютере в тетради а компьютере в тетради |
| Приложение 11 
| x | 0 | -1 | 1 | -2 | 2 | -3 | 3 | | y | 0 | 0,2 | 0,2 | 0,8 | 0,8 | 1,8 | 1,8 |
y = x2 | x | 0 | -1 | 1 | -2 | 2 | -3 | 3 | | y | 0 | 1 | 1 | 4 | 4 | 9 | 9 |
| Приложение 12 Построение в тетради на компьютере 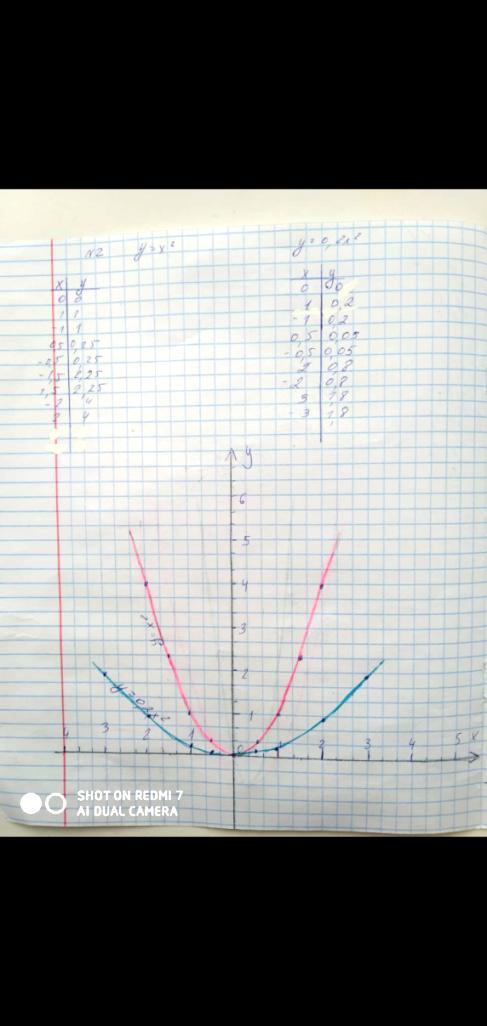 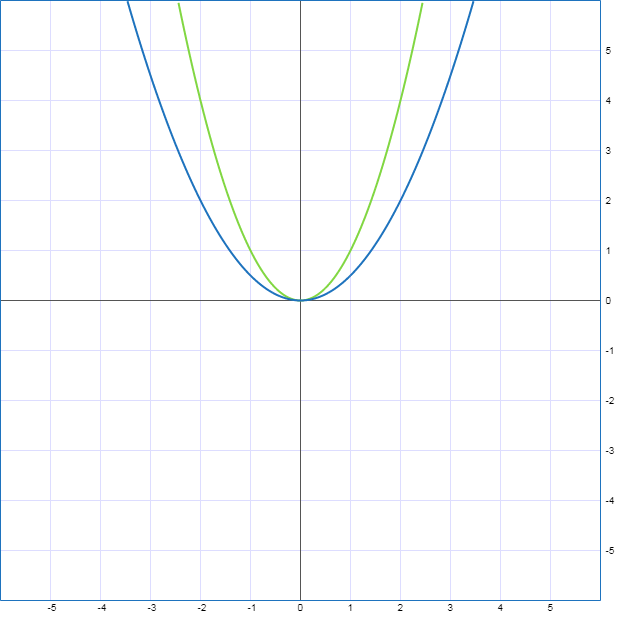
|
| Приложения 13 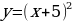
| x | 0 | -1 | -2 | -3 | -4 | -5 | -6 | -7 | -8 | | y | 25 | 16 | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
y = x2 | x | 0 | -1 | 1 | -2 | 2 | -3 | 3 | | y | 0 | 1 | 1 | 4 | 4 | 9 | 9 |
| П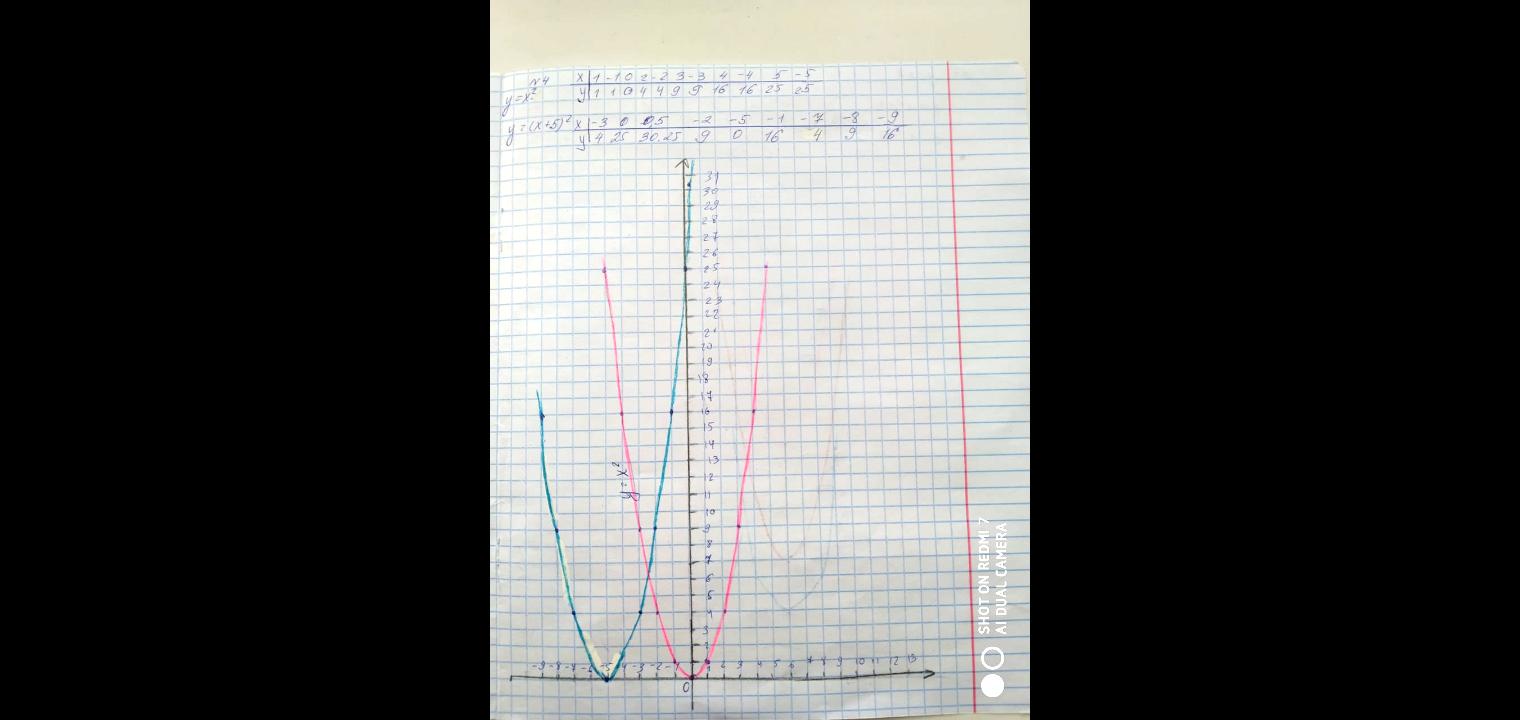 риложение 14 риложение 14 Построение на компьютере
в тетради |
| Приложение 15 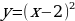
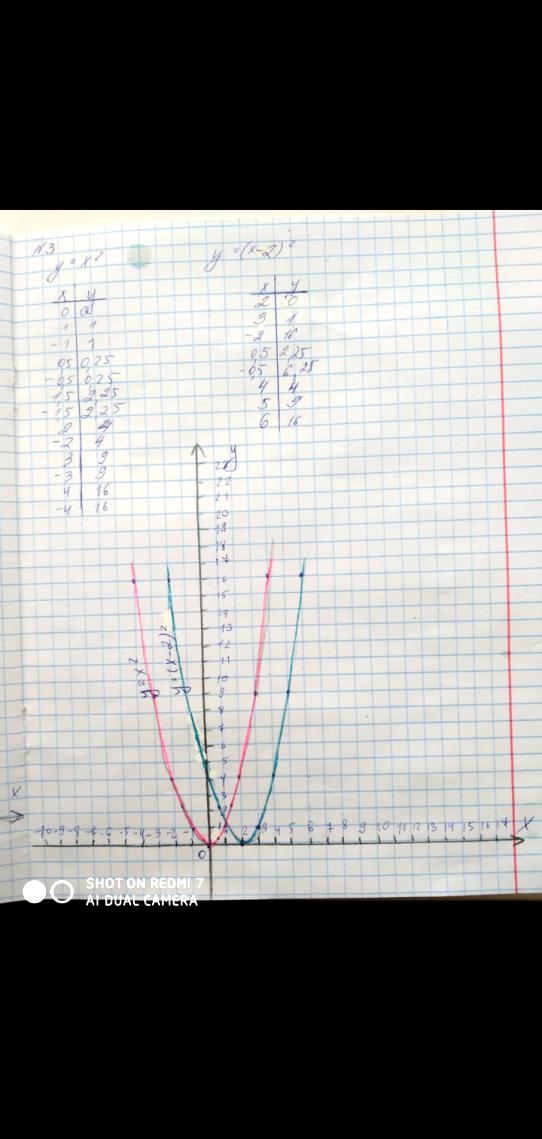
| x | 0 | -1 | 1 | -2 | 2 | -3 | 3 | | y | 4 | 9 | 1 | 16 | 0 | 25 | 1 |
y = x2 | x | 0 | -1 | 1 | -2 | 2 | -3 | 3 | | y | 0 | 1 | 1 | 4 | 4 | 9 | 9 |
| 
|
| Приложение 16 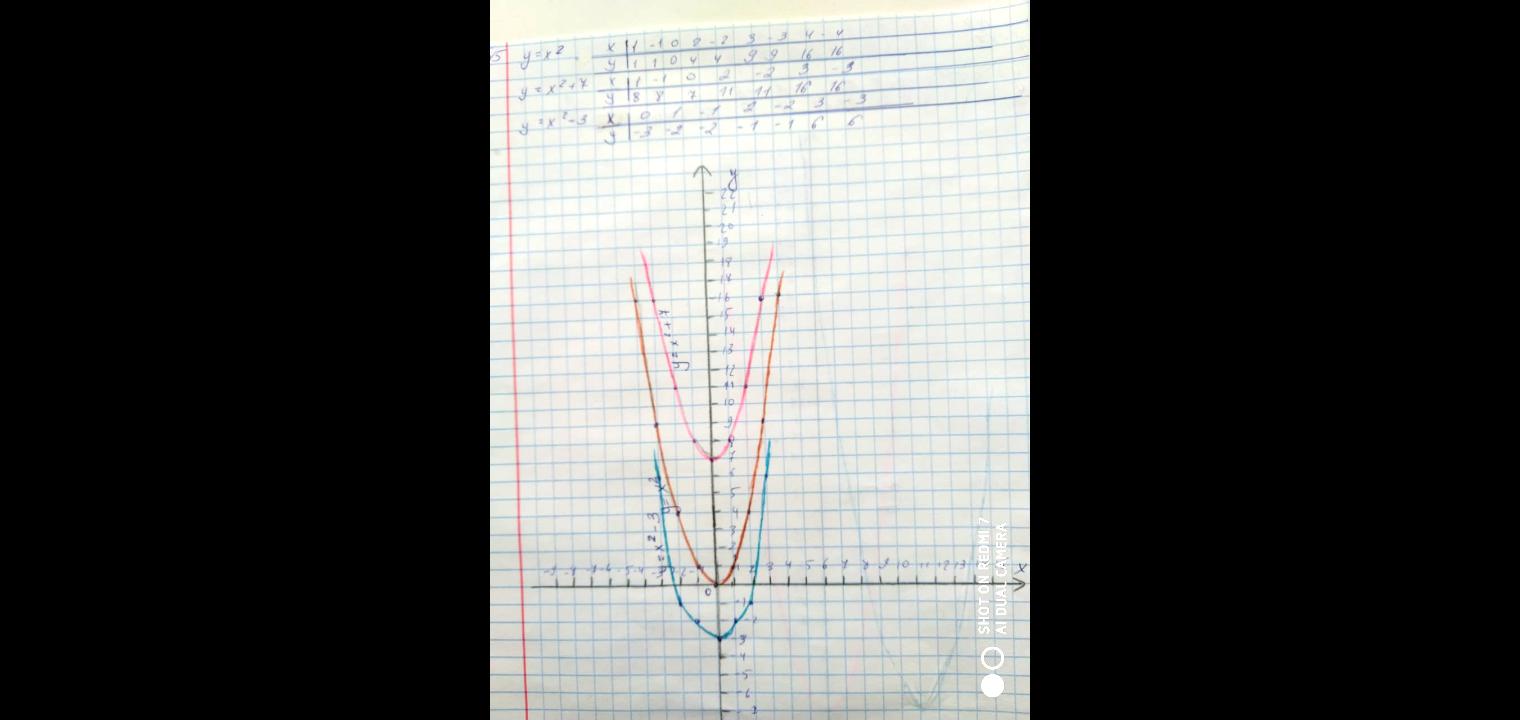
| П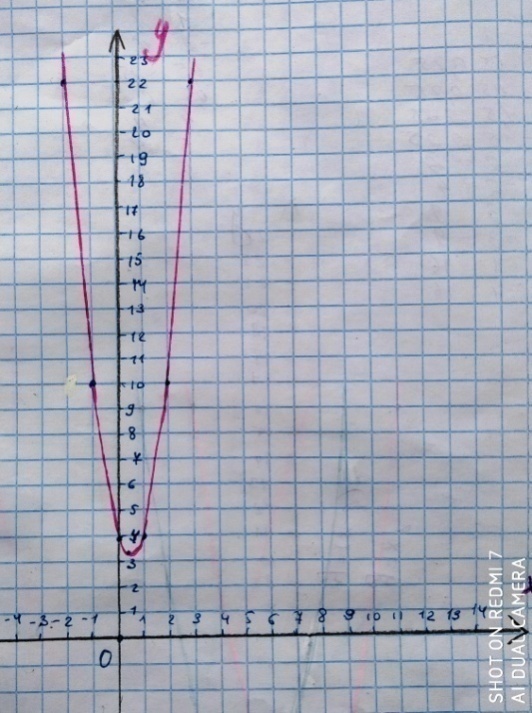 риложение 17 риложение 17
|
| П риложение 18 риложение 18 | Приложение 19

|
| Приложение 20 
| Приложение 21 
|
| Приложение 22 
| Приложение 23 
|
| Приложение 24 
| Приложение 25 
|
| Приложение 26

Тогучинский мост | Приложение 27

Бугримский мост в Новосибирске |
| Приложение 28 
| Приложение 29

|
| Приложение 30

|
| П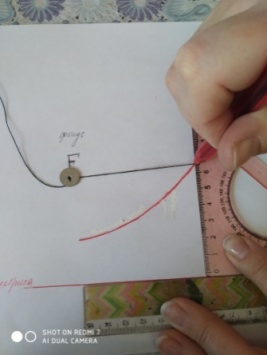 риложение 31 риложение 31 1) 2) 3)
  |
| Приложение 32 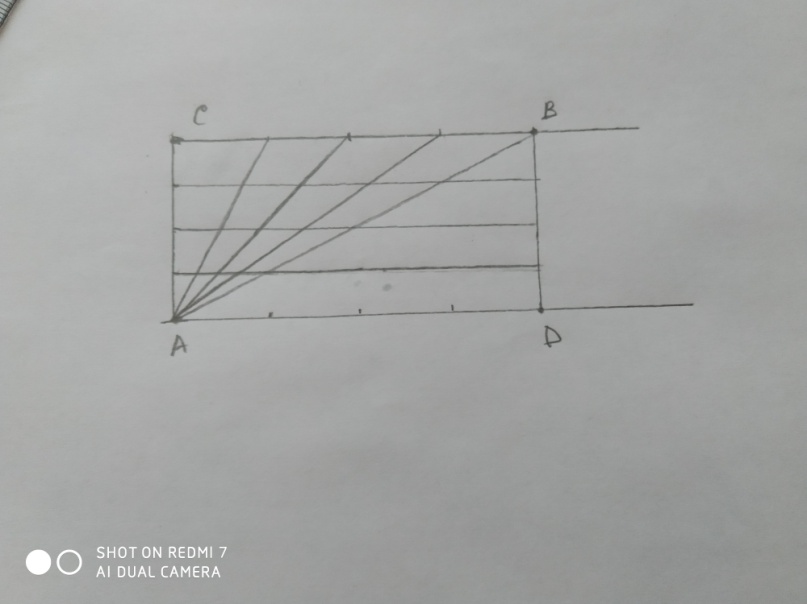 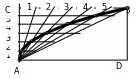 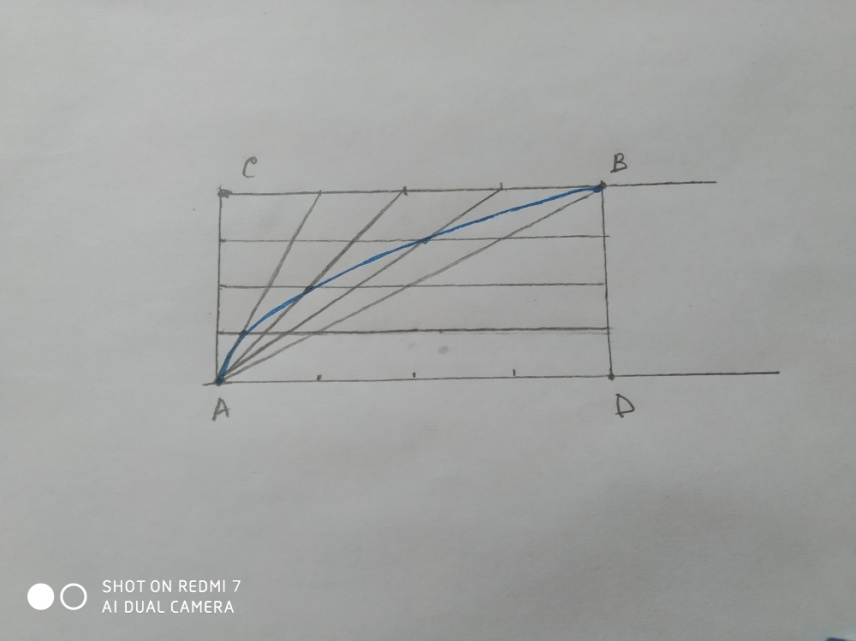
|
| Приложение 33 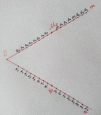 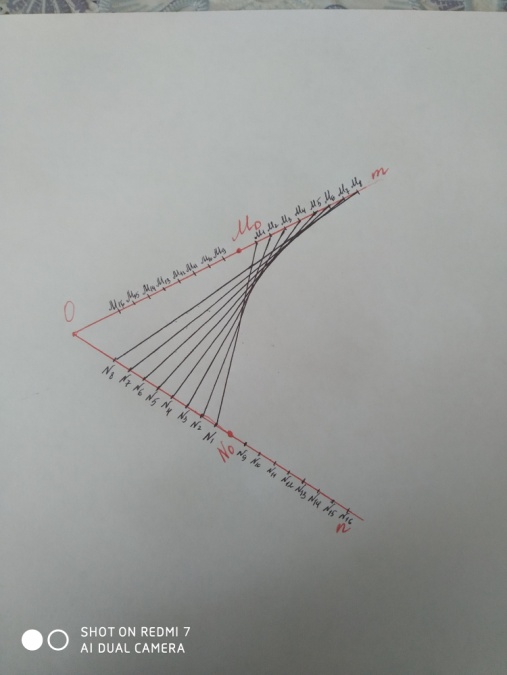 
|
| Приложение 34 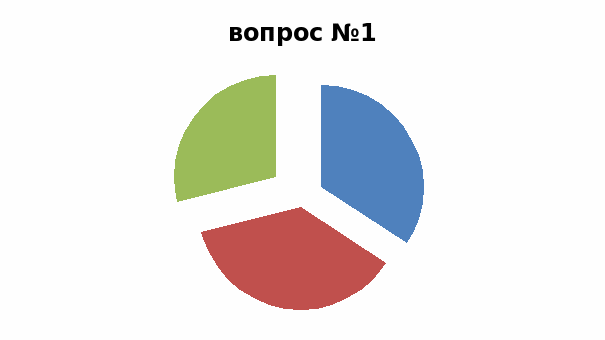 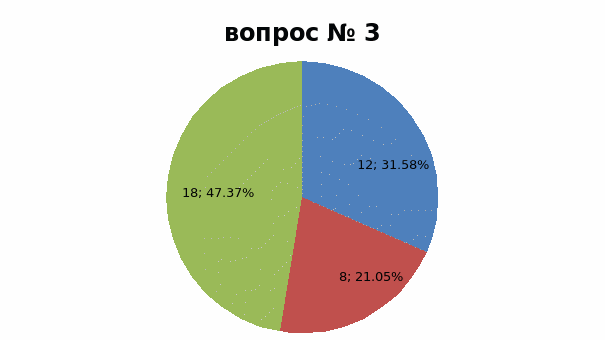
|
5







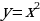 ,
, 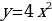 ,
,  ,
, 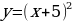 ,
, 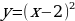
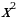 =0, при x=0
=0, при x=0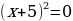 при x=-5
при x=-5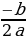 , xв =
, xв = 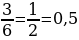 , yв = 3 * 0,52 – 3 * 0,5 + 4 = 3,25. Получилась координата вершины параболы (0,5; 3,25). Затем использовала для построения параболы таблицу и построила график функции по точкам (приложение 17).
, yв = 3 * 0,52 – 3 * 0,5 + 4 = 3,25. Получилась координата вершины параболы (0,5; 3,25). Затем использовала для построения параболы таблицу и построила график функции по точкам (приложение 17).








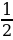
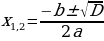 .
. 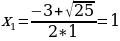 ,
, 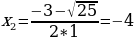 . Подставим в функцию y = -6x – 3 и найдем значения функции. у1 = -6 * 1 - 3 = - 9, у2 = - 6 * (- 4) – 3 = 21. Получили две точки пересечения параболы и прямой.
. Подставим в функцию y = -6x – 3 и найдем значения функции. у1 = -6 * 1 - 3 = - 9, у2 = - 6 * (- 4) – 3 = 21. Получили две точки пересечения параболы и прямой. 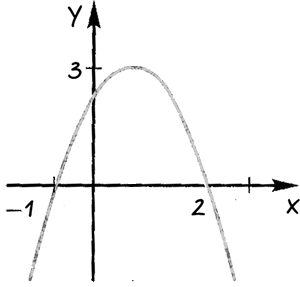 тобы по графику функции определить, где функция принимает положительные или отрицательные значения нужно:
тобы по графику функции определить, где функция принимает положительные или отрицательные значения нужно: ассмотрим пример, задан график функции, по графику определить при каких значениях х, функция принимает положительные и отрицательные значения.
ассмотрим пример, задан график функции, по графику определить при каких значениях х, функция принимает положительные и отрицательные значения. пределим области, где функция принимает отрицательные или положительные значения.
пределим области, где функция принимает отрицательные или положительные значения. одпишем над каждой полученной областью, какие значения принимает «x» в каждой из выделенных областей.
одпишем над каждой полученной областью, какие значения принимает «x» в каждой из выделенных областей.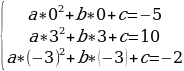
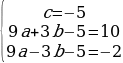
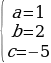 , составим формулу заданной квадратичной функции: y = x2 + 2x -5. Найдем для данной функции, координаты вершины, воспользуемся формулой
, составим формулу заданной квадратичной функции: y = x2 + 2x -5. Найдем для данной функции, координаты вершины, воспользуемся формулой 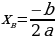 .
. 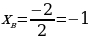 , yв = (-1)2 + 2*(-1) -5 = -6.
, yв = (-1)2 + 2*(-1) -5 = -6. 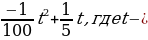 время, в минутах. Через какое время заполниться бассейн?
время, в минутах. Через какое время заполниться бассейн?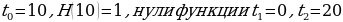 и учитывая жизненные условия, получим, что Таня перестанет плакать через 10 мин.
и учитывая жизненные условия, получим, что Таня перестанет плакать через 10 мин.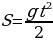 , g≈10 м/с2 (9,8 м/с2)
, g≈10 м/с2 (9,8 м/с2)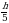 =
=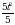 ; то 1c
; то 1c 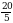 =4, то 2с и т.д.
=4, то 2с и т.д.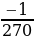 , b =
, b =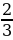 , с =
, с =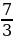 постоянные параметры. На каком максимальном расстоянии в метрах от забора нужно поставить машину, чтобы вода перелетала через верх? (приложение 29)
постоянные параметры. На каком максимальном расстоянии в метрах от забора нужно поставить машину, чтобы вода перелетала через верх? (приложение 29) 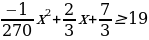 ,
,
 2)
2)  3)
3) 

 риложение 2
риложение 2 риложение 3
риложение 3 онтан
онтан  риложение 5
риложение 5 риложения 6
риложения 6



 а компьютере в тетради
а компьютере в тетради

 риложение 14
риложение 14


 риложение 17
риложение 17 риложение 18
риложение 18











 риложение 31
риложение 31