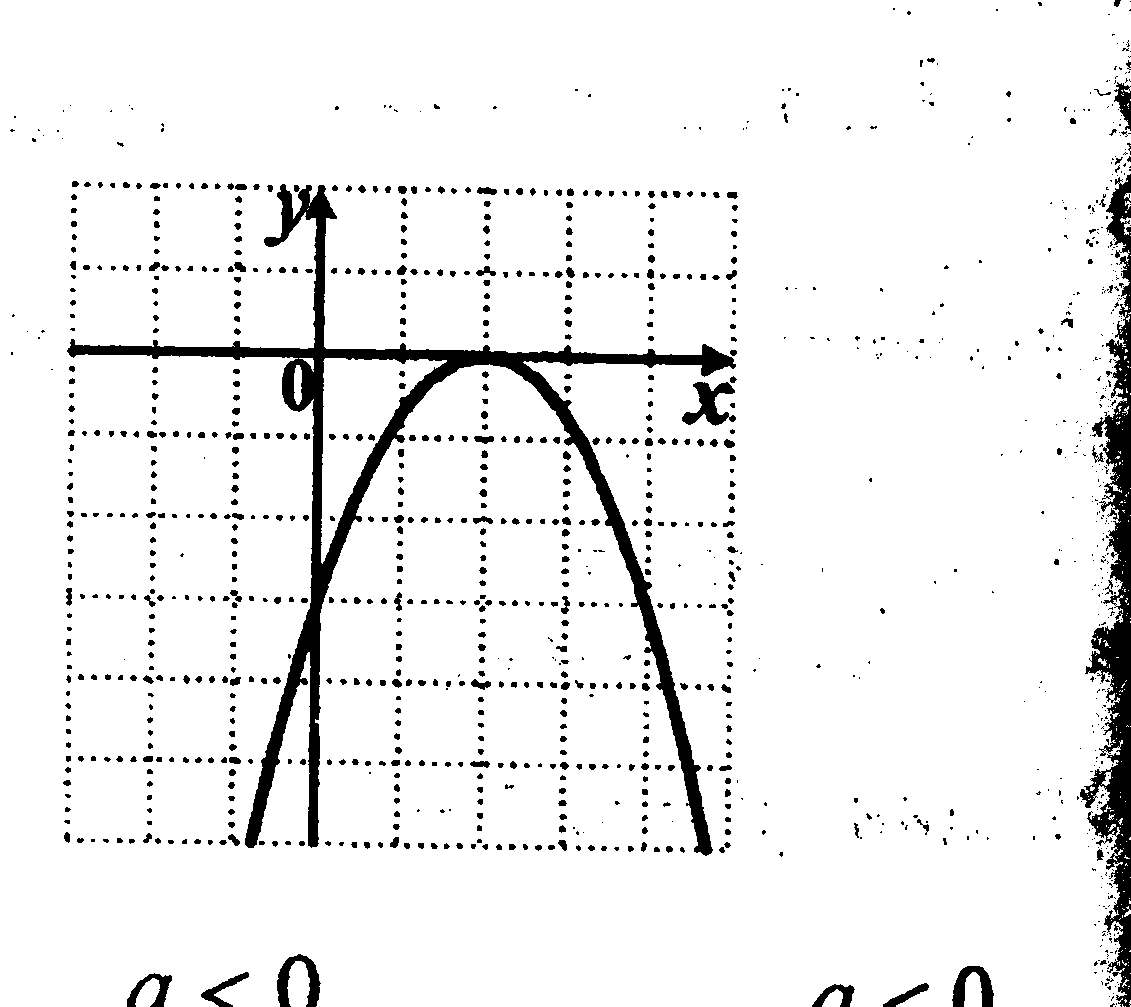Тема: «Квадратичная функция»
Цели урока:
образовательные: обобщить и систематизировать теоретические знания учащихся; совершенствовать знания, закрепить навыки решения задач по данной теме;
развивающие: развивать наблюдательность, логическое мышление, математическую речь учащихся, умение анализировать и сравнивать, осуществлять дифференцированное развивающее обучения, развивать познавательный интерес к предмету;
воспитательные: воспитывать коммуникативную культуру учащихся; навыки коллективной деятельности, сотрудничества, взаимопомощи, умение работать в парах.
Оборудование: интерактивная доска, карточки с заданием разноуровневой самостоятельной работы.
Тип урока: урок практической работы.
План урока:
Организационный момент
Устная работа
Решение разноуровневых заданий (с проверкой)
Проверочная самостоятельная работа
Итог урока
Домашнее задание
Историческая справка о Лейбнице
ХОД УРОКА
I Организационный момент. Сегодня у нас урок по теме «Квадратичная функция и ее график». Повторяем, обобщаем, приводим в систему изученный материал по данной теме. Ваша задача: показать свои знания, умения и навыки по данной теме при решении задач, при необходимости совершенствовать имеющиеся знания.
II Устная работа
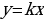
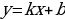
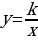

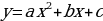
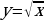
Вопросы:
Дать определение функции.
Что такое независимая переменная?
Что такое зависимая переменная?
Указать формулу, которой задается квадратичная функция, название графика.
Дать определение квадратичной функции.
Указать свойства функции: область определения, множество значений.
№1
Какие из этих графиков не являются графиками функций?
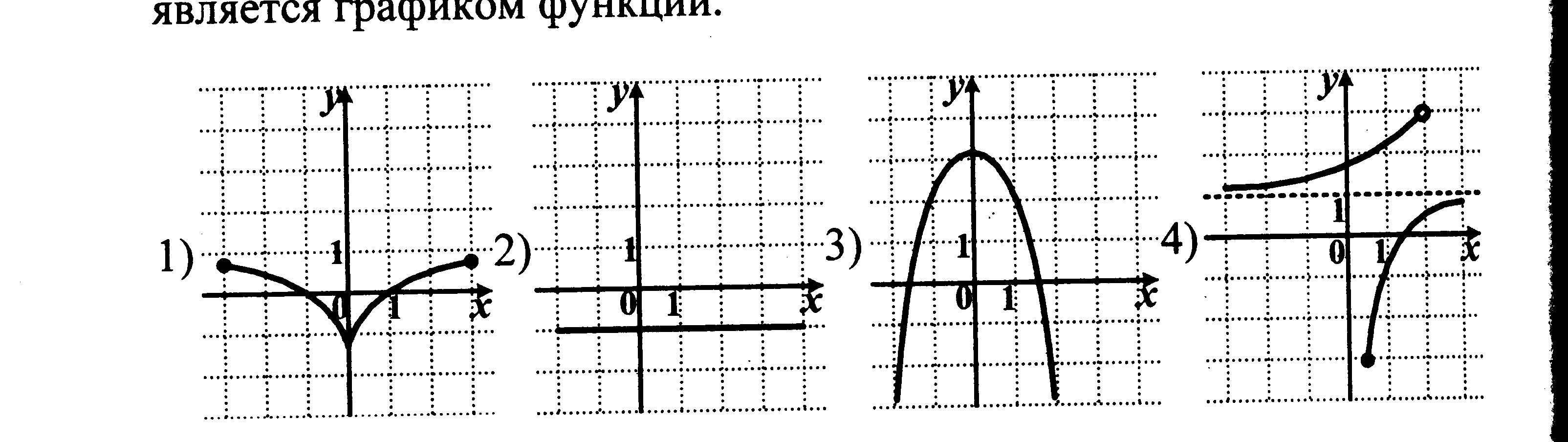 Ответ: 4
Ответ: 4
№2
Найдите соответствия
|
|
|
у = х2 – 5 |
у = 0,3х2 |
у = – (х – 3)2 |
у = – (х+ 2)2 +5
|
№3 На рисунке изображен график квадратичной функции. Какая из перечисленных формул задает эту функцию?
| 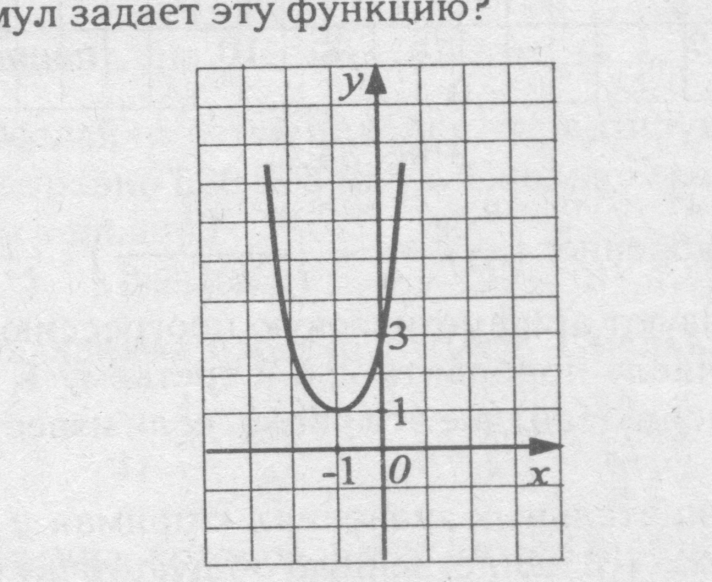
| у = – 2х2 +4х – 3 |
у = – 5х2 +10х + 3 |
у = х2 +2х + 3 |
у = 2х2 +4х + 3 |
|
|
№4
На рисунке изображен график квадратичной функции. Какая из перечисленных формул задает эту функцию?
| 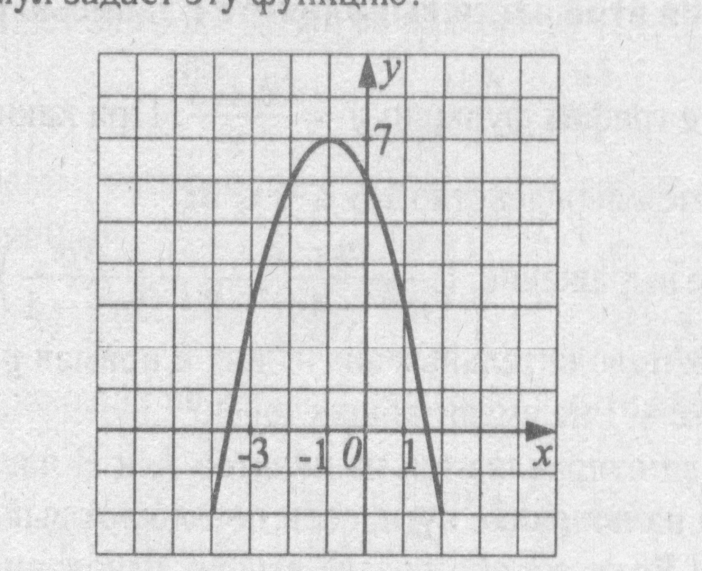
Что можете сказать о дискриминанте? | у = – х2 –2х + 6 |
у = – х2 +2х + 6 |
у = – х2 –2х + 8 |
у = – х2 +2х +8 |
|
|
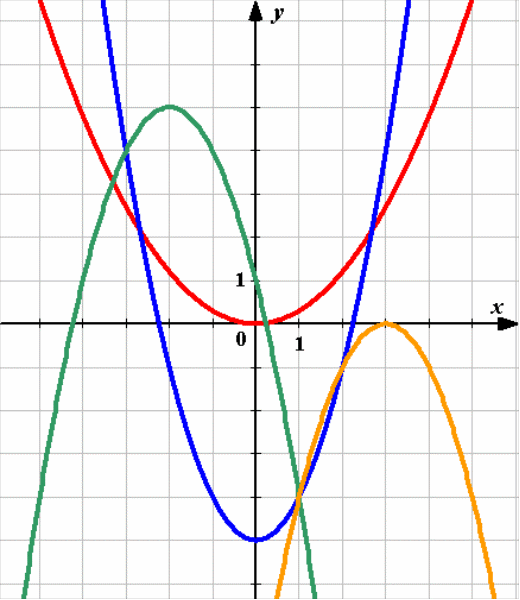
№5
На рисунке изображён график функции у = ах2 +bх + c. Определите знаки коэффициента а и дискриминанта D.
| 
| a 0, D 0 |
a 0, D 0 |
a 0, D 0 |
a 0, D 0 |
|
|
Ответ: 2
№6
На рисунке изображён график функции у = ах2 +bх + c. Определите знаки коэффициентов а, b и c.
III Решение разноуровневых заданий (с проверкой)
Карточка №1
Укажите координаты вершины параболы у = х2 +4х+ 1.
Решение.
х0 = 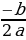 ; х0 =
; х0 = 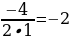 ; у0 = ( – 2)2 +4·(– 2) +1 = 4 – 8+1 = – 3.
; у0 = ( – 2)2 +4·(– 2) +1 = 4 – 8+1 = – 3.
Ответ: (– 2; – 3).
Карточка №2
Найдите координаты точек пересечения параболы у = х2 –3х + 2 с осями координат.
Решение.
Парабола пересекает ось ОУ (х = 0). Если х = 0, то у = 2.
Парабола пересекает ось ОХ (у = 0). Если у = 0, то х2 –3х + 2 = 0; х1 =1; х2 =2.
Ответ: (0;2); (1;0); (2;0).
Карточка №3
Найдите наименьшее значение функции у = 2х2 +4х – 3 при х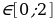 .
.
IV Проверочная работа (карточки)
Учащиеся самостоятельно выбирают оценку карточки для самостоятельной работы.
Карточки 3или 4
| 1 вариант Укажите координаты вершины параболы у = х2 –6х – 7. Найдите координаты точек пересечения параболы у = – 2х2 +3х – 1 с осями координат. Укажите верный набор неравенств для дискриминанта и коэффициентов a, b, c, если на рисунке изображен график функции у = ах2 +bх + c. 
a0, b0, D 0, c0 a 0, b 0, D 0 a 0, b 0, D 0 a 0, b 0, c 0, D
| 2 вариант Укажите координаты вершины параболы у = х2 +2х – 3. Найдите координаты точек пересечения параболы у = – х2 –2х + 3 с осями координат. Укажите верный набор неравенств для дискриминанта и коэффициентов a, b, c, если на рисунке изображен график функции у = ах2 +bх + c. 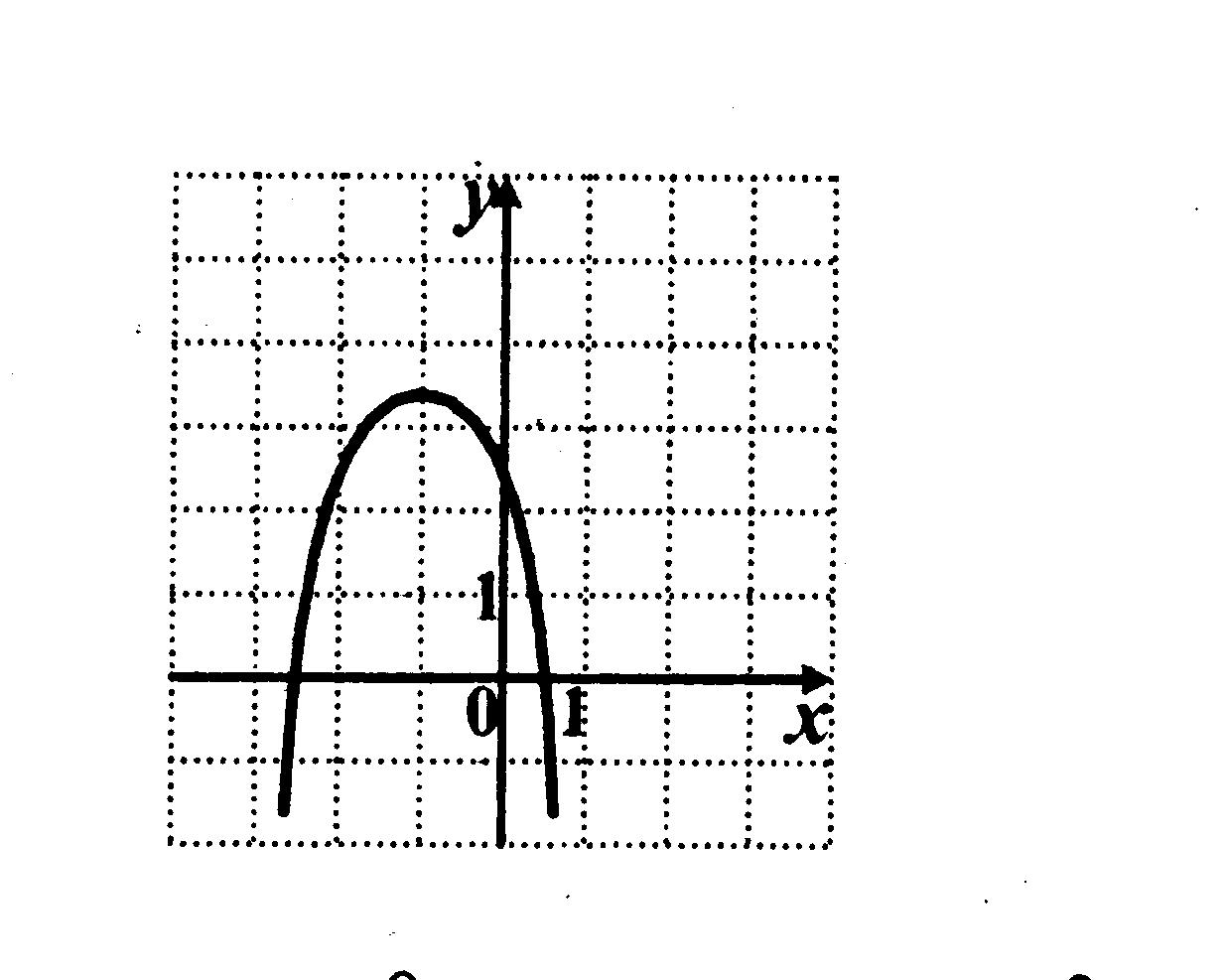
a 0, b 0, D 0, c 0 a 0, D 0, c 0 3)a 0 4)a 0, c
|
Карточки 4 или 5
вариант Укажите верный набор неравенств для дискриминанта и коэффициентов a, b, c, если на рисунке изображен график функции у = ах2 +bх + c. 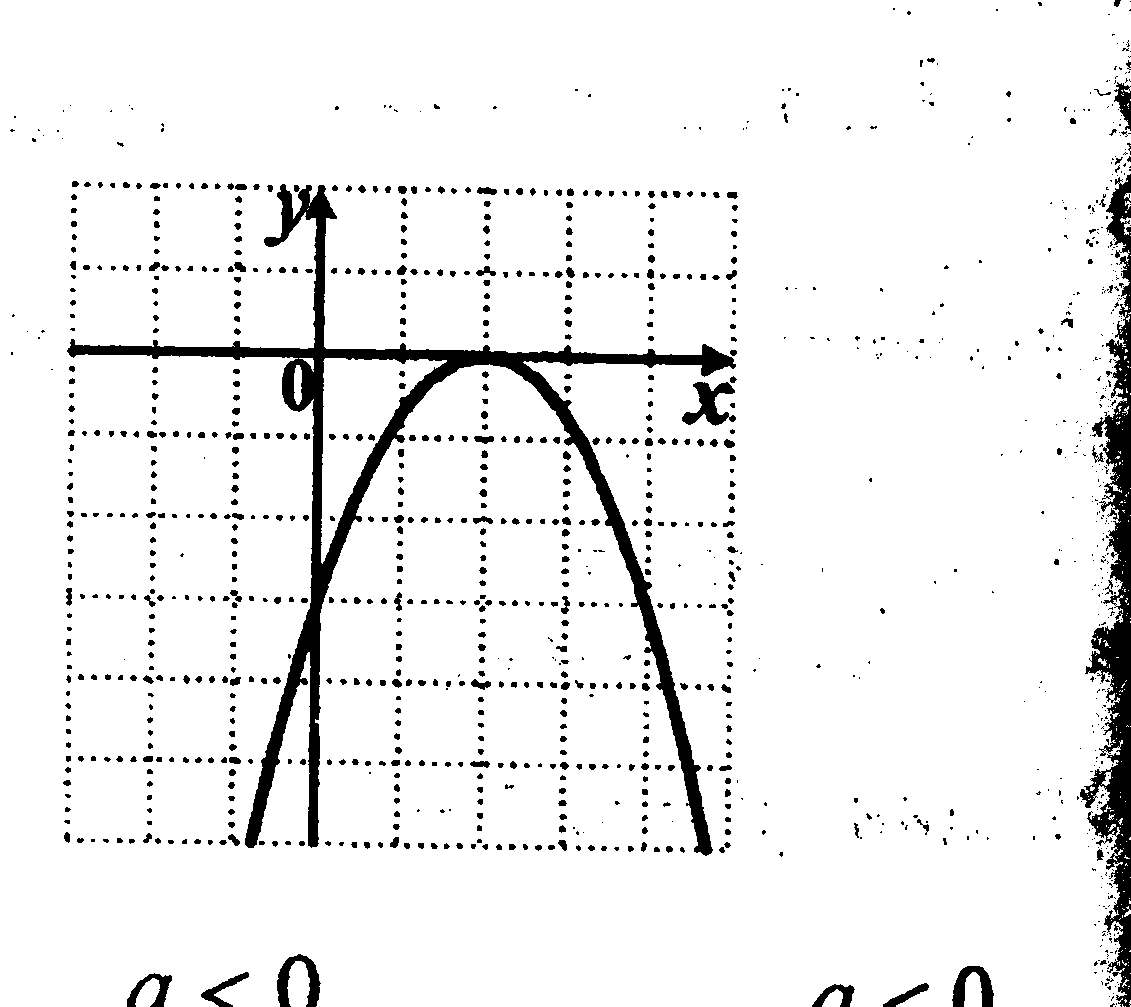
a 0, D 0 a 0, c 0, D 0 a 0, D = 0 a 0, c При каких значениях параметра а вершина параболы у = (6а – 5)х2 – 5х + 1 имеет отрицательную абсциссу?
| вариант Укажите верный набор неравенств для дискриминанта и коэффициентов a, b, c, если на рисунке изображен график функции у = ах2 +bх + c. 
a0, D 0, c0,b a 0, b 0, D 0, c 0 a 0, b 0, c a 0, b 0 При каких значениях параметра а вершина параболы у = 4х2– (–4а +1)х – 5 имеет отрицательную абсциссу? |
V Итог урока
Учитель подводит итог урока, оценивает работу учеников и ориентирует в домашнем задании.
VI Домашнее задание. Задание учителя






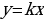
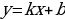
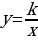

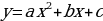
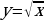
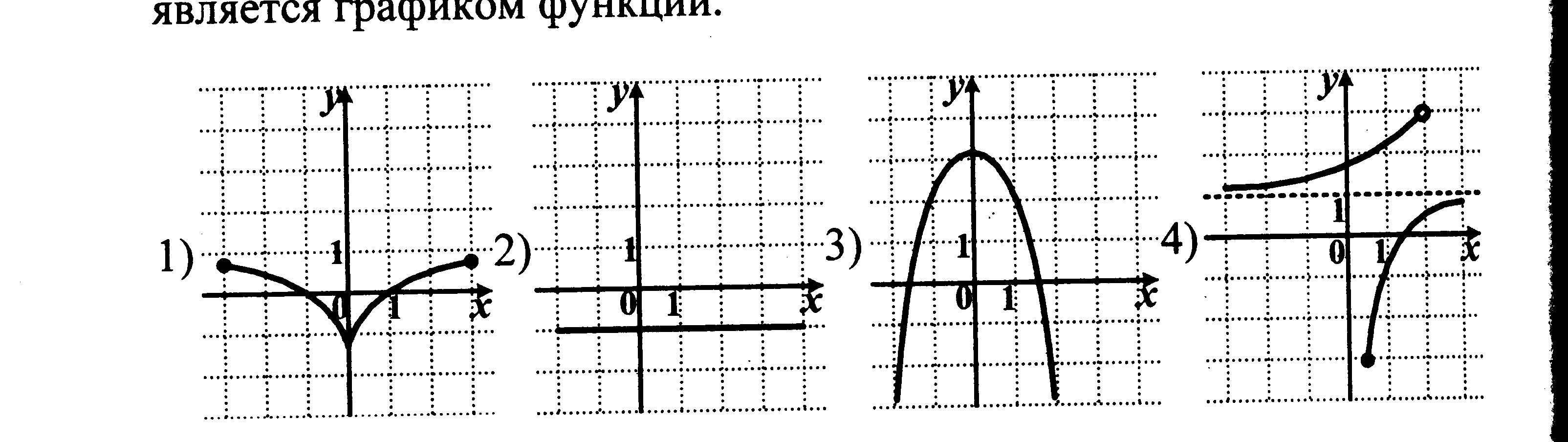 Ответ: 4
Ответ: 4



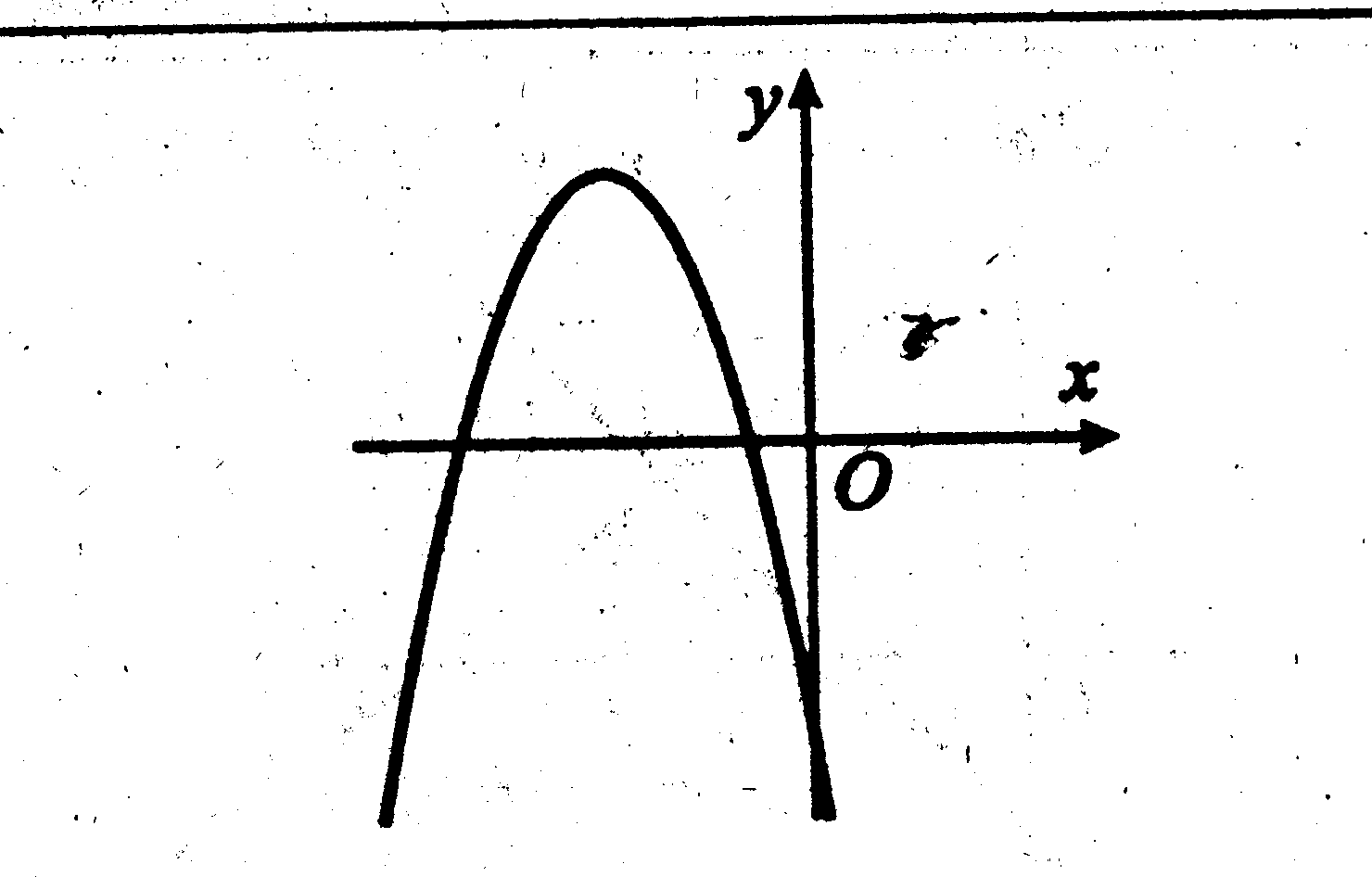
 ; х0 =
; х0 = 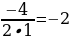 ; у0 = ( – 2)2 +4·(– 2) +1 = 4 – 8+1 = – 3.
; у0 = ( – 2)2 +4·(– 2) +1 = 4 – 8+1 = – 3.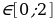 .
.