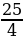Технологическая карта
открытого урока
по алгебре в 9 классе
на тему: «Квадратичная функция, ее график и свойства»
Провел: учитель математики
Аюбов Рамазан Курбанович
МКОУ «Талцухская СОШ», с. Талсух
МО Тляратинский район РД
Место проведения:
МКОУ «Талцухская СОШ»
Класс: 9
Дата проведения: 18.01.2021 г.
Учебник: Алгебра. 9 класс. Учебник для общеобразовательных организаций.
С.М. Никольский и др. – М., «Просвещение», 2016.
Цели урока: Обобщить и систематизировать основные знания, умения и навыки по теме «Квадратичная функция и её график», используя возможности ИКТ технологий и использовать эти знания для решения задач, входящих в раздел «Алгебра» ОГЭ .
Тип урока: урок – обобщения и систематизации изученного материла с использованием презентации и практической работы по теме «Квадратичная функция и её график».
Основные понятия, изучаемые на уроке: координатная плоскость, координата вершины параболы, дискриминант квадратного трехчлена, корни квадратного трехчлена, координаты точки пересечения графика с осью ординат, координаты точки пересечения двух графиков.
Технологии: проблемного обучения, развития исследовательских умений.
Формы организации деятельности учащихся на уроке: фронтальная работа с классом, индивидуальная работа, индивидуальная при закреплении материала, групповая работа при закреплении материала.
Цели:
образовательные:
-
находить координаты пересечения графика функции с осями системы координат;
-
находить координаты вершины параболы;
-
определение координат пересечения графиков двух функций;
-
формировать навыки самостоятельной работы;
развивающие:
- развивать навыки умений анализировать, сопоставлять и делать выводы;
- развивать познавательную активность, творческие способности обучающихся;
- развивать логическое мышление, математическую речь, навыки упрощения выражений.
воспитывающие:
-
воспитание интереса и любовь к предмету с привлечением мультимедийных возможностей компьютера;
-
содействовать в постановке самых высоких целей и достижению поставленной цели;
-
содействовать развитию умения общаться между собой и вести совместную работу;
-
развивать усидчивость, самостоятельность, самоконтроль, наблюдательность.
Оборудование:
- проектор, компьютер учителя.
Демонстрационный материал:
- презентация «Квадратичная функция»,
- папка с раздаточным материалом.
Раздаточный материал:
-
приложение №1: «Квадратичная функция»;
-
приложение №2: «Построение графика квадратичной функции»;
-
приложение №3: «Самостоятельная работа: Исследование графика квадратичной функции»;
-
приложение №4: «Совместная работа: График квадратичной и линейной функций»;
-
приложение №5: «Домашнее задание по теме: Координата середины отрезка»;
Требования к уровню подготовки обучающихся:
знать:
-
определение корня многочлена;
-
определение квадратного трехчлена;
-
определение квадратного уравнения;
-
определение квадратичной функции;
-
определение линейной функции.
уметь:
-
определять координаты вершины параболы;
-
определять корни трехчлена;
-
разложить многочлен на множители
-
строить график линейной функции.
Технологическая карта урока:
| Этап | Деятельность учителя | Деятельность учащихся | Формируемые умения |
| 1. Мотивационно-ориентировочный блок |
| 1.1. Мотивация к учебной деятельности. | Учитель приветствует учащихся. Читает эпиграф к уроку: Математика – самая надежная форма пророчества. В. Швебель (слайд 3). Как вы думаете, какую форму пророчества имел виду? В. Швебель? Мне бы хотелось, сегодня на уроке разобрать некоторые задания из КИМов ОГЭ, в частности задание 22. 22 задание ОГЭ по математике очень интересное и не самое сложное. Идеи заложенные в основе решения этой задачи довольно просты и нам нужно просто не боятся этого задания и пробовать его решить. Успешное решение этого задания обеспечить вам правильное выполнение еще 4 заданий из первой части ОГЭ Поэтому я надеюсь, что сегодня на уроке все будут активно работать.
Учитель читает высказывание А.Н. Крылова «Рано или поздно всякая правильная математическая идея находит применение в том или ином деле». (А.Н. Крылов) Как вы думаете: как вам и вашим родителям может помочь правильная математическая идея для успешной подготовки и сдачи ОГЭ?
Учитель обобщает рассуждения обучающихся и подводит итог беседы: Для успешной сдачи ОГЭ изучите таблицу Обобщённого плана вариант КИМ
основного государственного экзамена и ваши сильные и слабые стороны. | Записывают в тетради число, вид работы.
Высказывают предположения. Беседуют с учителем, между собой.
| Л: осознание необходимости получения новых знаний, мотивация познавательной деятельности. К: умения слушать, вступать в диалог, вырабатывать совместную точку зрения, участвовать в коллективном обсуждении. П: развитие мыслительных операций
|
| 1.2 Этап выделения проблемного поля и целеполагания | В настоящее время в нашей стране большое внимание уделяется вопросам повышения эффективности и качества во всех сферах производства. В этой связи особую значимость приобретает умение решать так называемые задачи на оптимизацию, которые возникают там, где необходимо выяснить как с помощью имеющихся средств достичь наилучшего результата, как получить нужный результат с наименьшей затратой средств, материалов, времени, труда и т.п.
Задание 7. При каких отрицательных значениях k прямая y = kx – 4 имеет с параболой y = x2 +3x ровно одну общую точку? Найдите координаты этой точки и постройте данные графики в одной системе координат.
(Уметь выполнять преобразования алгебраических
выражений, решать уравнения, неравенства и их сис-
темы, строить и читать графики функций, строить и
исследовать простейшие математические модели.) Читает высказывание Конфуция «Когда вам покажется, что цель недостижима, не изменяйте цель - изменяйте свой план действий» (слайд 7). Учитель систематизирует и обобщает выводы и ответы учащихся. Определить тему урока и образовательную цель урока. (слайд 2). Тема «Функции и их графики» Цели: -
Построение графика квадратичной функции. -
Определение коэффициентов квадратичной функции по его графику. -
Нахождение точек пересечения квадратичной и линейной функций |
Вступают в диалог с учителем. Предлагают варианты ответов на его вопросы.
Вступают в диалог с учителем. Предлагают варианты ответов на его вопросы
Анализируют информацию, проводят ее синтез, сравнивают, делают выводы. Формулируют тему "Функции и их графики» и цель "Учиться применять знания по изучаемой теме при решении практических задач".
Записывают тему урока. | К: умение высказывать собственные мысли, умение слушать и воспринимать другого, понимать собеседника. П: умение перерабатывать информацию, выделять существенные признаки Р: самостоятельное выделение и формулирование целей. Л: личностное самоопределение, осознание необходимости получения новых знаний. |
| 2. Организационно-деятельностный блок |
| 2.1 Этап актуализации опорных знаний и фиксация проблемы при выполнении заданий | Выдаёт на каждую парту по четыре листа с заданиями (листы разных цветов).
Давайте вспомним, какую функцию называют квадратичной и алгоритм построения графика квадратичной функции?
Задание 1. На рисунке изображены графики функций вида y = ax2 + bx + c. Для каждого графика укажите соответствующее ему значения коэффициента a и дискриминанта D (2431); Даны четыре графика квадратичной функции. Для каждого графика определить промежутки возрастания(убывания) функции, наибольшее(наименьшее) значение. - А умеете ли вы определять координаты точек? Определите координаты вершины и точки правее от вершины на 1. (слайд 4, 5). Задание 2. Найдите координаты вершины параболы функции у = x2 -4x+3. (слайд 6).
Организует и контролирует работу учащихся.
Выявить, зафиксировать и решить проблемную ситуацию: проверят задание на листах самоконтроля и презентует правильное решение.
- Молодцы! Вы прекрасно поработали.
| Самостоятельно выполняют задание №1 и задание №2 в листе самоконтроля (приложение 1).
К доске вызывается ученик, который презентует свою работу с помощью документ камеры. Остальные учащиеся проверяют решение и оценивают свою работу.
Учащиеся, которые выполнили задания передают листы.
Вспоминают определение и свойства квадратичной функции. Записывают формулы для нахождения вершины параболы. Находят координаты вершины параболы и точки правее вершины. | Л: оценивание усвоенного раннее материала. Р: формирование умений планировать своё действие в соответствии с поставленной задачей. П: активизация опорных знаний и умений |
|
|
|
|
|
| 2.2 Этап формирование новых знаний и умений. (Объяснение новой темы)
|
Предлагаю более детально разобрать и обсудить, алгоритм построения графика квадратичной функции и связь между коэффициентами и графиком квадратного трехчлена. -
Что мы должны знать про каждый коэффициент? -
Как найти коэффициенты по графику функции?
Предлагаю, для этого, решить задачу пару задач.
Задание 3. Найдите значение а, b и с по графику функции у = ах2+bx+c, изображенному на рисунке. 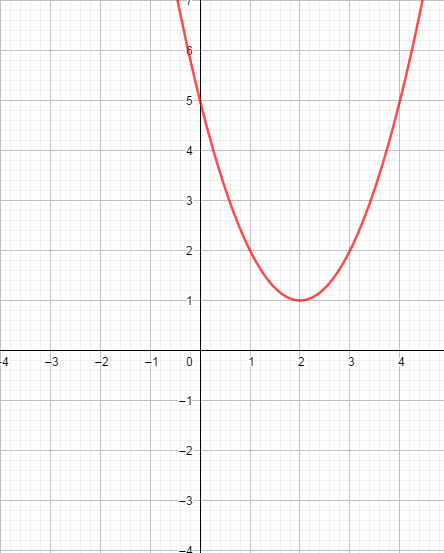
(слайд 8).
I. Нахождение коэффициента a: 1) по графику параболы определяем координаты вершины (m, n) 2) по графику параболы определяем координаты любой точки А(х;у) 3) подставляем эти значения в формулу квадратичной функции, заданной в другом виде: y=a(х-m)2+n 4) решаем полученное уравнение относительно а. Или f(m+1) – f(m) II. Нахождение коэффициента b: -
Сначала находим значение коэффициента а; -
В формулу для абсциссы параболы m= -b/2a подставляем значения m и a; -
Находим значение коэффициента b. Замечание. Если а и b одного знака, то вершина слева от оси Ох. (Если а и b разного знака, то вершина справа от оси Ох). III. Нахождение коэффициента с: -
Находим ординату у точки пересечения параболы с осью Оу, это значение равно коэффициенту с; -
Если по графику невозможно найти точку пересечения с осью Оу, то выполняем шаги I, II (находим коэффициенты a, b) -
Подставляем найденные значения a, b , А(х ;у) в уравнение у=ax2 +bx+c и находим с.
Задание 4. При каких отрицательных значениях k прямая y = kx – 4 имеет с параболой y = x2 +3x ровно одну общую точку? Найдите координаты этой точки и постройте данные графики в одной системе координат. (слайд 9-13 )
Сделайте вывод: уравнять правые части двух функций и решить уравнение.
Предлагает составить алгоритм решения подобных задач.
| Вступают в диалог с учителем. Предлагают варианты текста задачи и в ходе коллективного обсуждения приходят к выводу:
Вступают в диалог с учителем. Отвечают на его вопросы. Записывают выражение, для нахождения координат параболы. Алгоритм построения графика квадратичной функции: -
определить направление ветвей параболы (коэффициент а); -
вычислить координаты вершины параболы (m; n) по формулам х0 = 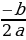 , у0 = y (x0) или у0 = - , у0 = y (x0) или у0 = - 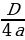 . (m . (m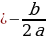 , n = , n = 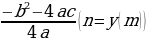 и построить в системе координат; и построить в системе координат; -
провести ось симметрии параболы (x = m); -
найти нули функции, если они есть (дискриминант D), решив квадратное уравнение; -
найти точку пересечения с осью Оу (коэффициент с); -
найти и построить дополнительные точки с учетом оси симметрии параболы; -
провести через построенные точки параболу. Для нахождения точек пересечения графиков двух функций надо приравнять правые части обоих функций и решить получившееся уравнение.
Отвечают на вопрос учителя и делают вывод: -
коэффициент а отвечает за направление ветвей параболы и определяется по координатам двух точек параболы; -
Коэффициент с – ордината точки пересечения параболы с осью Оу; -
Растяжение графика вдоль оси Оу относительно оси Ох при а 1 (сжатие при 0
Вступают в диалог с учителем. Предлагают варианты последовательности действий.
Составляют алгоритм решения подобных задач: -
уровнять правые части функций и решить уравнение; -
построение графиков функций.
(приложение 4)
| П: умения логически рассуждать, делать умозаключение, формирование интереса к теме. Л: готовность к самообразованию, осознание личной ответственности за результат; умение переносить предметные знания на другие сферы деятельности человека. К: умение слушать и вступать в диалог, участвовать в коллективном обсуждении, давать полный ответ, доказывать свою точку зрения. Р: планирование своей деятельности для решения поставленной задачи. |
| 2.3 Этап первичного усвоения новых знаний и закрепления темы.
| Учитель предлагает обучающимся по составленным двум алгоритмам действий решить следующие задачи:
Задание 5. Найдите значение а и с по графику функции у = ах2+bx+c, изображенному на рисунке. (слайд 14)
Управляет познавательной деятельностью обучающихся, оказывает дозированную помощь
|
Обучающиеся работают парами. Выполняют решение в листе самоконтроля Учащиеся, первыми решившие задачу правильно, выходят к доске, с помощью документ камеры презентуют свою работу. Остальные учащиеся проверяют решение и оценивают свою работу.
| Р: осознание того, что усвоено, а что подлежит усвоению; структурирование собственных знаний. П: умение действовать в соответствии с предложенным алгоритмом; К.: умение сотрудничать в парах, принимать на себя роль консультантов и экспертов, выслушивать мнение напарника. Л: умение работать в паре, аргументация своего мнения. |
| Физкультминутка (для глаз) |
| 2.3 Этап самостоятельной работы с самопроверкой по эталону. | Учитель предлагает обучающимся решить следующую задачу:
Задание 6. Найдите все значения k, при каждом из которых прямая y = kx имеет с графиком функции y = x2 + 4 ровно одну общую точку. Постройте этот график и все такие прямые. (слайд 15-16). Управляет познавательной деятельностью обучающихся, оказывает дозированную помощь. Организует обсуждение итогов работы, уточняет и дополняет ответы обучающихся. | Решают задачу самостоятельно в листах самоконтроля. Выполняют взаимопроверку по слайду презентации, оценивают свою работу. (слайд 8).
| Р: отличать способ и результат своих действий с заданным эталоном, обнаруживать отклонения и отличия от эталона. Л: находчивость, активность при решении задач; умение оценивать свои достижения П: умение применять полученные знания для решения задач; развитие мыслительных операций
|
| 2.4 Этап применения знаний в нестандартной ситуации. | Учитель предлагает обучающимся: -
сформулировать план (алгоритм) решения следующей задачи: -
решить задачу. Задание 7. Постройте график функции y = 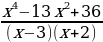 и определите, при каких значениях параметра c прямая y = c имеет с графиком ровно одну общую точку. и определите, при каких значениях параметра c прямая y = c имеет с графиком ровно одну общую точку. (слайд 17-18).
Учитель организует обсуждение плана решения задачи, уточняет и дополняет план. | Составляют и формулируют план решения задачи. Решают задачу и проверяют решение по образцу. (слайд 11) | Р: структурирование собственных знаний; Л: находчивость, активность при решении задач; П: умение применять полученные знания для решения задач. |
| 3. Рефлексивно-оценочный блок |
| 3.1 Рефлексия учебной деятельности
| В успехе нет ничего магического или загадочного. Успех – это результат ежедневного выполнения простых правильных действий. (Джим Рон.) (слайд 19).
- Ребята, давайте вспомним основные понятия, с которыми мы с вами познакомились при изучении темы «Функции и графики функций».
Предлагает учащимся вспомнить, какую цель ставили в начале урока. Спрашивает, достигли ли ее. Согласны ли с эпиграфом. Организует рефлексию. Предлагает из облака слов выбрать наиболее значимые слова для каждого ученика и записать с их помощью свое отношение к работе на уроке
|
Соотносят полученную информацию с той, что была у них в начале урока, выясняют на какие вопросы найдены ответы, а на какие еще нет. Составляют свое маленькое резюме о своей работе на уроке. Оценивают свою работу на уроке в листах самоконтроля и сдают его учителю. | Л: умение оценивать свои достижения, выявлять причины неудачи. К: умение адекватно оценивать результат, сотрудничать со сверстниками и учителем. П: умение сопоставлять цель и результат |
-
Объяснение домашнего материала |
| 4.1 Домашнее задание | Предлагает записать домашнее задание (приложение 5). (слайд 20). Критерии оценки домашнего задания: одна задача – «3», две задачи – «4», три задачи – «5» Благодарит за работу. | Формулируют уточняющие вопросы учителю, записывают в дневники домашнее задание. | Саморегулирование |
Л – личностиные УУД
П – позновательные УУД
Р – регулятивные УУД
К – коммуникативные УУД.
Литература:
1. Примерные программы по учебным предметам. Математика. 5-9 классы. – М.: Просвещение, 2011. – 64 с. – (Стандарты второго поколения).
2.Учебник «Алгебра – 9» под редакцией А.Г. Мерзляка, В.Б. Полонского и др.
3.Методическое пособие для учителя Е.В.Буцко, А.Г.Мерзляк к учебнику.
4.https://infourok.ru/zadachi-na-optimizaciyu-316174.html
5.htt ps://rvb.ru/tolstoy/01text/vol_10/01text/0259.htm - МНОГО ЛИ ЧЕЛОВЕКУ ЗЕМЛИ НУЖНО
6.https://www.bibliofond.ru/view.aspx?id=789718
7. https://wordart.com/create
Приложение №1
Задание 1. На рисунке изображены графики функций вида y = ax2 + bx + c. Для каждого графика укажите соответствующее ему значения коэффициента a и дискриминанта D.
| Графики А) Б) 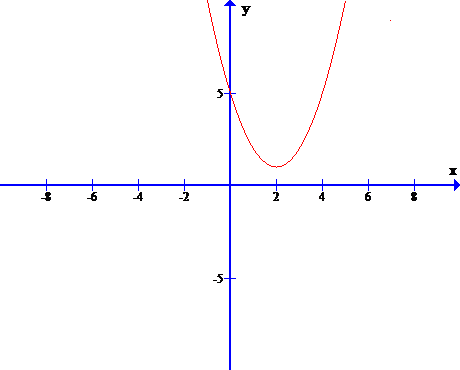 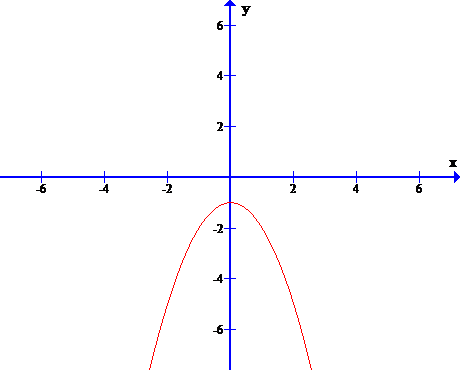 С В) Г)
 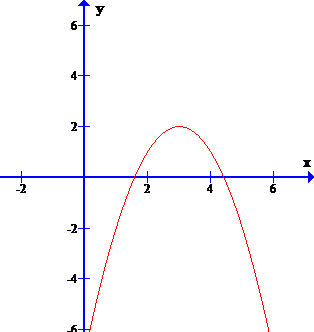 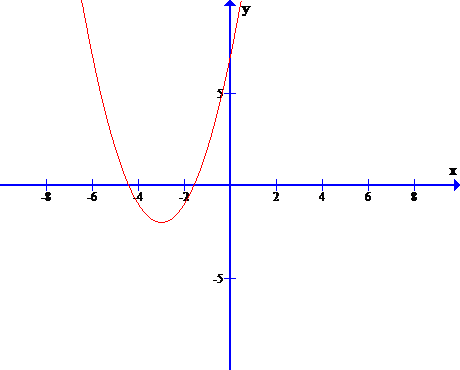
Знаки чисел | 1) a 0, D 0 | 2) a 0, D | 3) a D 0 | 4) a D | Запишите в ответ цифры, расположив их в порядке, соответствующем буквам: |
Задание 2. Найдите координаты вершины параболы функции у = x2 – 4 x +3.
ПЛАН ПОСТРОЕНИЯ ГРАФИКА
квадратичной функции y = ax2 + bx + c
-
определить направление ветвей параболы (коэффициент а);
-
вычислить координаты вершины параболы (m; n) по формулам
х0 = 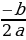 , у0 = y (x0) или у0 = -
, у0 = y (x0) или у0 = - 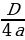 . (m
. (m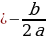 , n =
, n = 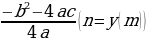 и построить в системе координат;
и построить в системе координат;
-
провести ось симметрии параболы (x = m);
-
найти нули функции, если они есть (дискриминант D), решив квадратное уравнение;
-
найти точку пересечения с осью Оу (коэффициент с);
-
найти и построить дополнительные точки с учетом оси симметрии параболы;
-
провести через построенные точки параболу.
Приложение 2.
Задание 3. Найдите значение а, b и с по графику функции у = ах2+bx+c, изображенному на рисунке.

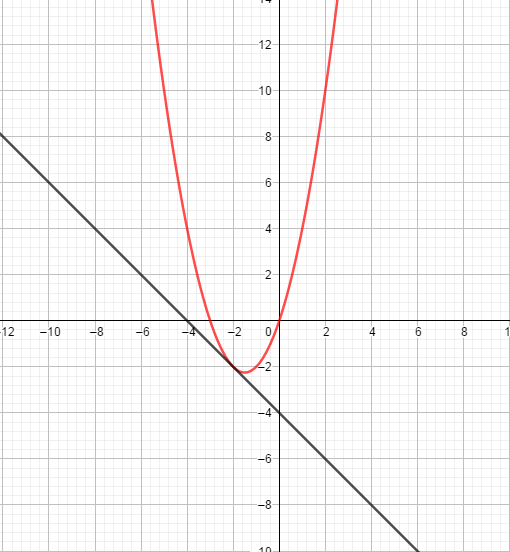
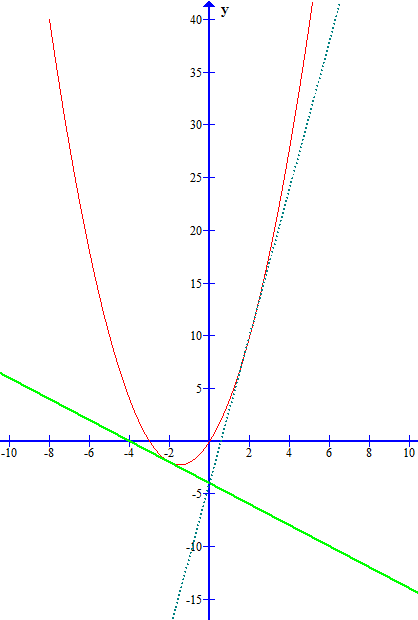
Задание 4. При каких отрицательных значениях k прямая y = kx – 4 имеет с параболой y = x2 +3x ровно одну общую точку? Найдите координаты этой точки и постройте данные графики в одной системе координат.
Решение.
Запишем условие общей точки: kx – 4 = x2 + 3x x2 + (3–k)x + 4 = 0.
Для того, чтобы прямая и парабола имели одну общую точку необходимо, чтобы дискриминант равнялся нулю. Дискриминант равен: (3-k)2 -16 = 0, откуда (3-k)2 = 16. Он обращается в ноль при k = −1 или k = 7. По условию необходимо отрицательное k, таким образом, k = −1. Построим графики функций: y = –x–4 и y = x2 +3x
Ответ: k = −1, координата точки: (−2;−2).
Приложение 3.
Задание 5. Найдите значение а и с по графику функции у = ах2+bx+c, изображенному на рисунке.
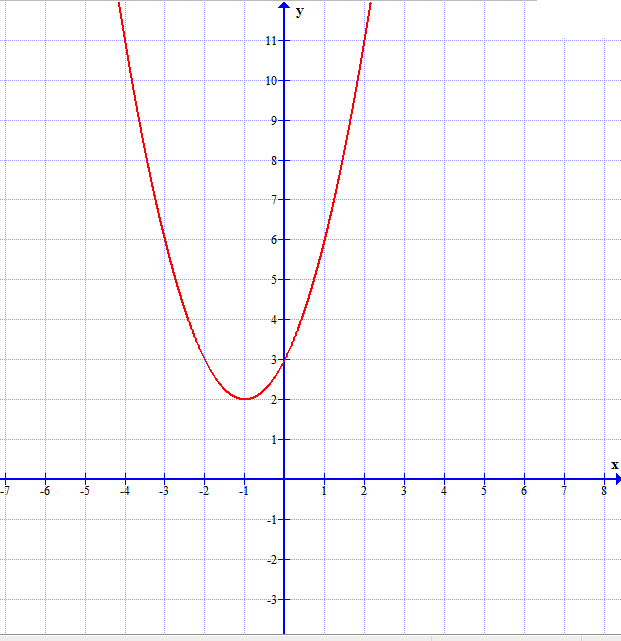
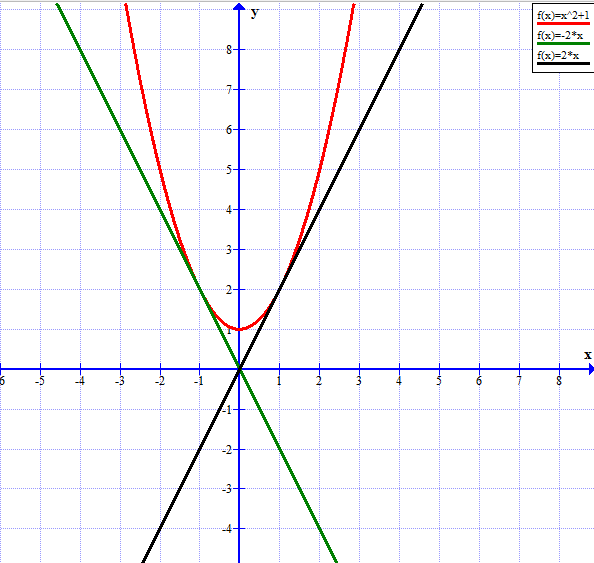
Задание 6. Найдите все значения k, при каждом из которых прямая y = kx имеет с графиком функции y = x2 + 4 ровно одну общую точку. Постройте этот график и все такие прямые.
Решение.
Построим график функции:
График функции y = x2 + 1 получается из графика функции y = x2 сдвигом на (0;1).
Прямая y = kx имеет с этим графиком ровно одну общую точку, если уравнение
x2 + 1 = kx имеет один корень. Дискриминант этого уравнения равен k2 − 4, и он должен быть равен нулю. Получаем, что k = −2 или k = 2.
Графики прямых y = 2x и y = −2x строятся по точкам.
Ответ: −2; 2.
Задание 7. Постройте график функции y = 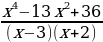 и определите, при каких значениях параметра c прямая y = c имеет с графиком ровно одну общую точку.
и определите, при каких значениях параметра c прямая y = c имеет с графиком ровно одну общую точку.
Решение.
Пусть t = x2 тогда числитель принимает вид t2 - 13t +36. По теореме, обратной теореме Виета, сумма корней уравнения t2 - 13t +36 = 0 равна 13, а их произведение — 36. Тем самым, это числа 4 и 9. Тогда по формуле ax2 + bx + c = a(x-x1) (x-x2) получаем:
t2 - 13t +36 = (t – 4)(t – 9).
Возвращаясь к исходной переменной, имеем:
x4 – 13x2 + 36 = (x2 – 4) (x2 – 9) = (x – 2)(x + 2)(x – 3)(x + 3).
Сократим дробь: при x - 2 и x 3 функция принимает вид: y=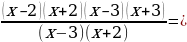 (x – 2)(x + 3) = x2 + x – 6
(x – 2)(x + 3) = x2 + x – 6
y = (x – 2)(x + 3) = x2 + x – 6, её график — парабола c выколотыми точками (-2;-4) и (3;6).
Выделим полный квадрат: у = x2 + x – 6 = x2 +2х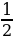 +
+ 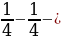 6 = (х+
6 = (х+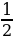 )2 -
)2 - 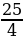
Следовательно, искомая парабола получается сдвигом графика функции y = x2 на (-0,5;-6,25).
Прямая имеет у = с имеет с этой параболой ровно одну общую точку либо тогда, когда проходит через вершину параболы, либо тогда, когда пересекает параболу в двух точках, одна из которых — выколотая. Вершина параболы имеет координаты (-0,5;-6,25), ординаты выколотых точек суть у(-2) = 4 – 2 - 6 = - 4 и y(3) = 9 + 3 – 6. Поэтому c = - 6,25, c = - 4 или c = 6.
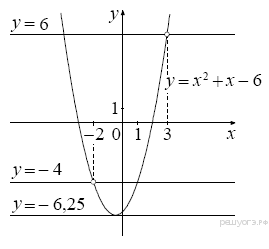
Ответ: c = - 6,25, c = - 4 или c = 6.
Источник: Демонстрационная версия ГИА—2013 по математике.
Домашнее задание.
Задание 8. При каких значениях b прямая y = b имеет с параболой y = x2 +2x ровно одну общую точку? Найдите координаты этой точки и постройте в одной системе координат данную параболу и прямую при найденном значении b.
Задание 9. При каких значениях p прямая y = -2x + p имеет с параболой y = x2 +2x ровно одну общую точку? Постройте в одной системе координат данную параболу и прямую при найденном значении p.
Задание 8. При каких значениях b прямая y = b имеет с параболой y = x2 + x ровно одну общую точку? Найдите координаты этой точки и постройте в одной системе координат данную параболу и прямую при найденном значении b.
Решение.
Запишем условие общей точки: x2 +2x = b x2 + 2x – b = 0.
Прямая y = b будет иметь с параболой y = x2 +2x единственную общую точку при условии, что дискриминант полученного квадратного уравнения равен нулю:
4 + 4b = 0 откуда b = –1. Подставив значение параметра в уравнение, находим
x = –1, y = –1.
Построим в одной системе координат прямая y = -1 и параболу y = x2 +2x
Ответ: b = −1, координата точки: (−1; −1).
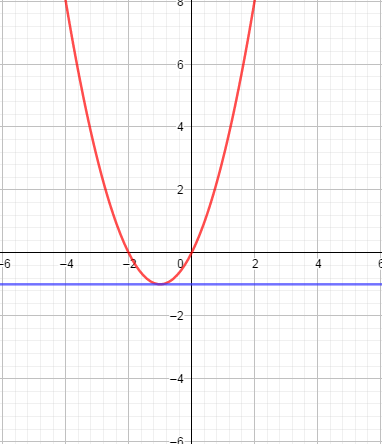
Задание 9. При каких значениях p прямая y = -2x + p имеет с параболой y = x2 +2x ровно одну общую точку? Постройте в одной системе координат данную параболу и прямую при найденном значении p.
Решение.
Запишем условие общей точки: – 2x + p = x2 +2x x2 + 4x – p = 0.
Прямая y = – 2x + p будет иметь с параболой y = x2 +2x единственную общую точку при условии, что дискриминант полученного квадратного уравнения равен нулю:
16 + p = 0 откуда p = - 4. Подставив значение параметра в уравнение, находим
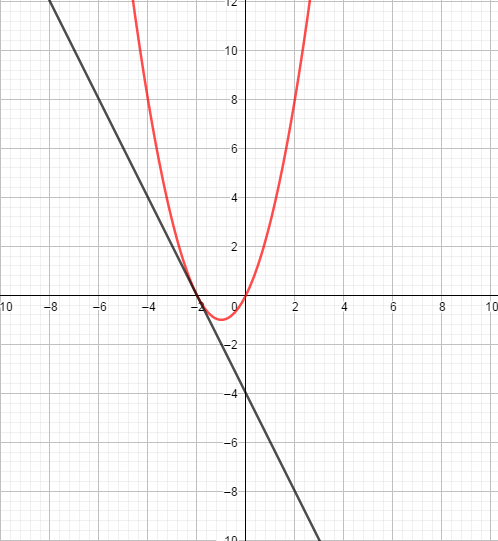
x = - 2, y = 0.
Ответ: p = −4, координата точки: (−2; 0).
МУНИЦИПАЛЬНОЕ КАЗЕННОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«ТАЛЦУСКАЯ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА»

Технологическая карта открытого урока
по алгебре в 9 классе на тему:
«Квадратичная функция, ее график и свойства»
Провел: учитель математики
Аюбов Рамазан Курбанович
с. Талсух, МО Тляратинский район РД
Место проведения:
МКОУ «Талцухская СОШ»
Класс: 9
Дата проведения: 18.01.2021 г.
6








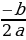 , у0 = y (x0) или у0 = -
, у0 = y (x0) или у0 = - 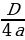 . (m
. (m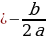 , n =
, n = 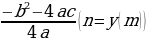 и построить в системе координат;
и построить в системе координат;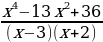 и определите, при каких значениях параметра c прямая y = c имеет с графиком ровно одну общую точку.
и определите, при каких значениях параметра c прямая y = c имеет с графиком ровно одну общую точку.








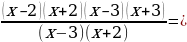 (x – 2)(x + 3) = x2 + x – 6
(x – 2)(x + 3) = x2 + x – 6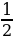 +
+ 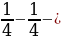 6 = (х+
6 = (х+