

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

Квадратичная функция. Построение графика квадратичной функции
Категория:
Математика
06.01.2017 17:46




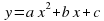 называется квадратичной, (
называется квадратичной, (
 – коэффициент при старшей степени неизвестной х,
– коэффициент при старшей степени неизвестной х, – коэффициент при неизвестной х,
– коэффициент при неизвестной х,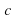 - свободный член.
- свободный член.

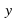
 .
. ,
, 


 .
. . Для этого приравниваем нашу функцию к нулю
. Для этого приравниваем нашу функцию к нулю
 . Далее следует один из трех возможных вариантов:
. Далее следует один из трех возможных вариантов: , то парабола пересекает ось
, то парабола пересекает ось 

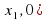 и (
и (










