Квадратный корень из произведения и дроби

МБОУ «СОШ с.Генеральское»

Квадратный корень из

произведения и дроби

Разработка урока по математике в 8 классе

Журило Наталия Геннадьевна

учитель математики,

высшая категория

2014

Тема урока: Квадратный корень из произведения и дроби

Цели урока: изучение свойств квадратных корней из произведения и дроби, формирование умений применения этих свойств для вычисления значений квадратных корней, закрепление вычислительных навыков.

Тип урока: урок изучения нового материала

Вид урока: мультимедийный урок

Оборудование: мультимедийный проектор,таблица по теме, карточки для самостоятельной работы, учебник «Алгебра 8» под ред. Теляковского С.А., 2010

ХОД УРОКА

1. Организация урока. (Доска закрыта. Внутри неё уже записана тема урока).

Здравствуйте, ребята! Поприветствуйте наших гостей! (кивком головы)

1. Постановка цели урока

А начнём мы наш урок с устной разминки. Давайте попробуем, решая примеры, найти среди них «незнакомые», «нерешаемые», и попытаемся сами определить тему и цели нашего урока… Итак,

1. Устная работа (Слайд 1)

1. Возведите в степень:

а) ( х³ )⁵ ;

б) ( -2а )³ ;

в) ( х² / у³ )⁴ ;

г) (16 )² ;

д) ( 36 )² ;

е) ( 3 ^. 2 )² ;

ж) √32*98. (последний пример не знаком, выписывают его в тетрадь и на доску)

2. Вычислите: (Слайд 2)

а) 100;

б) 0,0064;

в) 16/81;

г) 0,25;

д) 1;

е) 400;

ж) 121;

з) 0;

и) (97 - 93)( 97 + 93 );

к) √36/121. (последний пример не знаком, выписывают его в тетрадь и на доску).

2. Беседа.

- А теперь прочитайте мне эти записанные выражения математическим языком.

(квадратный корень из произведения чисел 32 и 98; квадратный корень из дроби 36/121).

-Итак, тема нашего урока сегодня…. (открываем доску) - Квадратный корень из произведения и дроби. (Записывают тему в тетрадь)

- Какие цели мы ставим перед собой на этом уроке? (Научиться находить квадратный корень из произведения и дроби).

- Помним про девиз «Цель вижу, в себя верю!»

1. Актуализация опорных знаний и умений

– Сформулируйте определение арифметического квадратного корня.

- Равенство а = b является верным, если выполняются 2 условия. Какие?

- При каких значениях а выражение а имеет смысл?

- Чему равен квадрат арифметического квадратного корня (а)² = ?

- Сформулируйте свойство степени произведения.

- Сформулируйте свойство степени дроби.

III.Изучение нового материала (Открытие новых знаний)

Слайд 3

- Сегодня мы изучим свойства квадратного корня – квадратный корень из произведения и дроби.

Слайд 4

Сравним значения выражений  814 и 814.

 814 =  324 = 18; 814 = 9  2 = 18.

- Какой можно сделать вывод?

(Значит,  814 = 814.)

Слайд 5

-Совершенно верно. А сможем ли мы сформулировать эту запись математическим языком? (Корень из произведения равен произведению корней из каждого множителя). Об этом нам гласит 1-я Теорема.

Слайд 6

Теорема I. Если а  0, b  0, то ab = а b.

Доказательство: Пусть a³0, b³0. Тогда Öab и Öa ·Öb имеют смысл. Покажем, что

1) Öa·Öb³0; 2) (Öа · Öb) ² = ab.

Т.к. а³0, то Öa³0; b³0, то Öb³0. Значит, Öa · Öb ³0.

(Öa·Öb) ² = (Öa)² · (Öb) ² = ab.

Значит, Öab = Öa · Öb, где a ³0, b ³0.

Это справедливо не только для произведения двух множителей, но и больше двух.

Öabc = Öa · Öb · Öc, где a ³0, b ³0, с ³0.

Корень из произведения неотрицательных множителей равен произведению корней из этих множителей.

Запись в тетради и на доске:

Теорема 1. Если а  0, b  0, то ab = а b.

Слайд 7

А рискнёт ли кто-нибудь из вас предположить, как найти квадратный корень из дроби?

(Может быть, нужно извлечь корень и из числителя, и из знаменателя?)

Слайд 8

Теорема 2. Если a³0 и b0, то Öа/b = а /  b.

Доказательство: Так как a³0, то Öa³0, т.к. b0, то Öb0. Значит, a / b  0. Тогда

(a / b)² = (a )² / (b)² = а/b. Значит, Öа/b = а /  b, где a³0 и b0.

Корень из дроби, числитель которой неотрицателен, а знаменатель положителен, равен корню из числителя, деленному на корень из знаменателя.

Запись в тетради и на доске:

Теорема 2. Если a³0 и b0, то Öа/b = а /  b.

Слайд 9

Рассмотрим примеры:

1. Ö64·0,04= Ö64 · Ö0,04= 8 · 0,2 = 1,6

2. Ö32 · 98 = Ö( 16 · 2) · (49 · 2 ) = = Ö 16 · 49 · 4= Ö16 · Ö49 · Ö4 = 4·7·2=56

3.  (36/121) = 36 / 121 = 6/11.

IV. Закрепление изученного материала

Слайд 10

№ 369 (а, в, д), 370 (а, в, д, е) – у доски и в тетрадях;

№ 372 (а, в, г) – комментарий с места

V. Самостоятельная работа

Задания в карточках

Вариант 1.

1. Найдите значение выражения:  0,36 ^. 81.

А. 5,4. Б. 54. В. 0,54. Г. 1,34.

2. Найти значение выражения:  16 ^. 49 ^. 0,25 .

А. 140. Б. 28. В. 2. Г. 14.

3. Вычислите: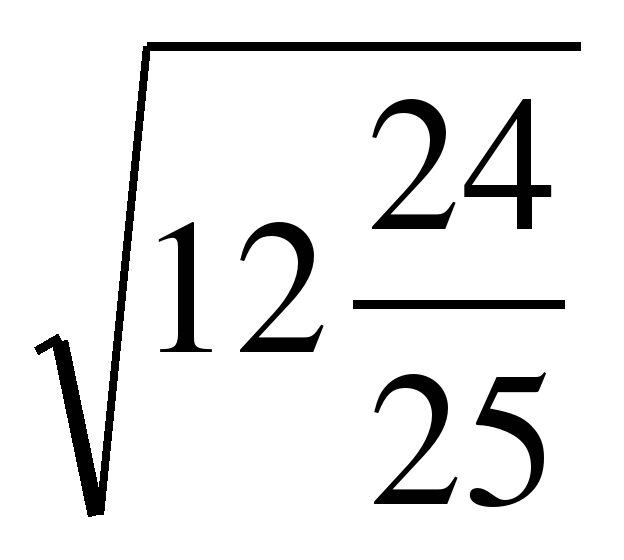

А. 1,2. Б. _. В. 3,6. Г. .

Вариант 2.

1. Найдите значение выражения:  0,64 ^. 25.

А. 4. Б. 16. В. 8. Г. 40.

2. Найти значение выражения:  25 ^. 16 ^. 0,36 .

А. 120. Б. 144. В. 72. Г. 12.

3. Вычислите: .

А. 7,25. Б. 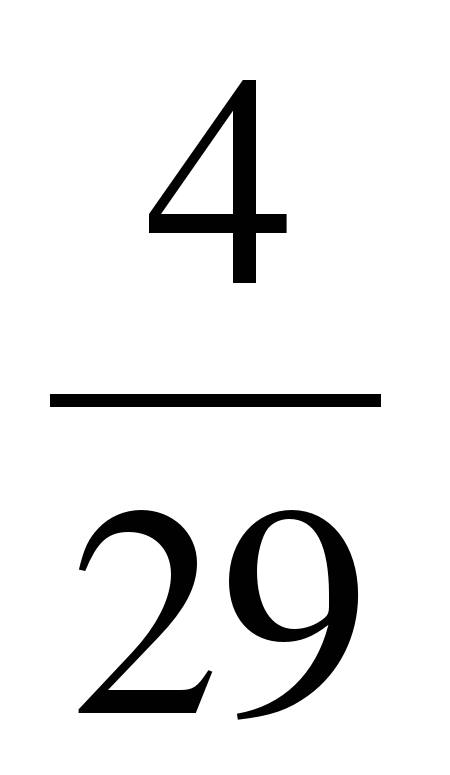_. В. 7,5. Г. .

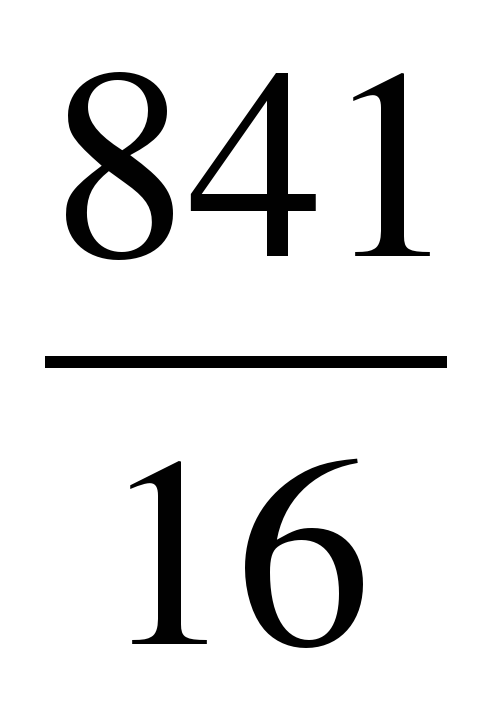VI. Дома: п. 15, № 371, 373.

VII. Итог урока. Выставление оценок.

ПРИЛОЖЕНИЕ

Фамилия, имя_____________________________________

Вариант 1.

1. Найдите значение выражения:  0,36 ^. 81.

А. 5,4. Б. 54. В. 0,54. Г. 1,34.

2. Найти значение выражения:  16 ^. 49 ^. 0,25 .

А. 140. Б. 28. В. 2. Г. 14.

3. Вычислите: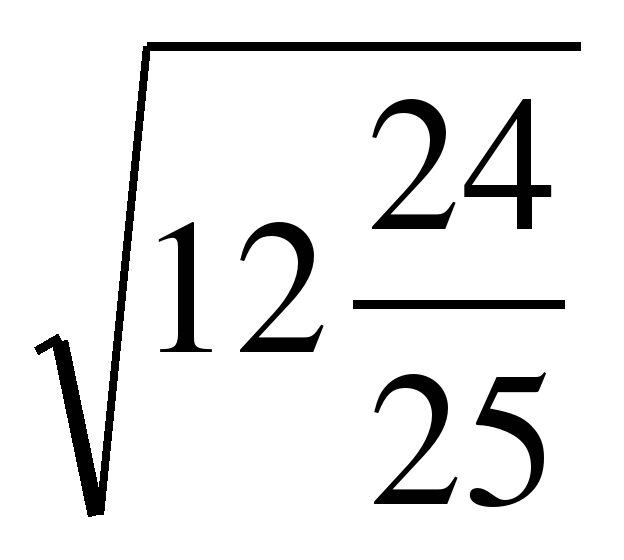

А. 1,2. Б. _. В. 3,6. Г. .

Фамилия, имя_____________________________________

Вариант 2.

1. Найдите значение выражения:  0,64 ^. 25.

А. 4. Б. 16. В. 8. Г. 40.

2. Найти значение выражения:  25 ^. 16 ^. 0,36 .

А. 120. Б. 144. В. 72. Г. 12.

3. Вычислите: .

А. 7,25. Б. 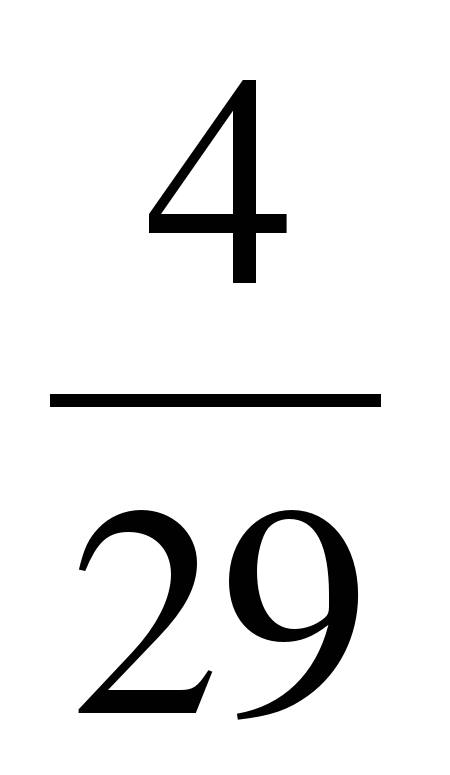_. В. 7,5. Г. .

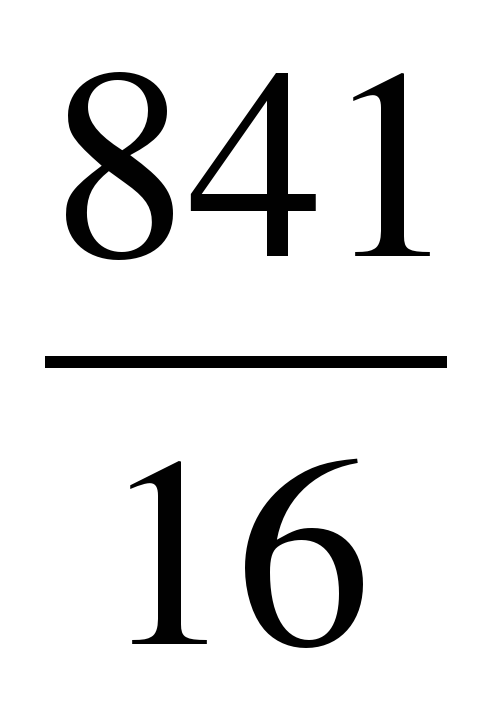• 1. Возведите в степень:
• а) ( х3 )5 ;
• б) ( -2а )3 ;
• в) ( х2 / у3 )4 ;
• г) (  16 )2 ;
• д) ( 3  6 )2 ;
• е) (  3 *  2 )2 ;
• ж) √32*98.

• а)  100;
• б)  0,0064;
• в)  16/81;
• г)  0,25;
• д)  1;
• е)  400;
• ж)  121;
• з)  0;
• и) (  97 -  93)(  97 +  93 );
• к) √36/121 .

Квадратный корень из произведения и дроби

п.16, стр. 84

1 . Сформулируйте определение арифметического квадратного корня.

2. Равенство  a = b является верным, если вы -полняются 2 условия. Какие?

3. При каких значениях a выражение  a имеет смысл?

4. Чему равен квадрат арифметического квадратного корня (  a) =?

2

5. Сформулируйте свойство степени произведения.

6. Сформулируйте свойство степени дроби.

Сравним значения выражений  81·4 и  81 ·  4

18.

 324 =

 81 · 4 =

18.

 81 ·  4 =

9 · 2 =

 81 · 4 =  81 ·  4 .

Чему равен корень из произведения двух множителей?

 81 · 4 =  81 ·  4 .

Теорема 1. Если a  0 и b  0 , то  ab=  a ·  b

Доказательство:

Пусть a  0 , b  0. Тогда  ab и  a ·  b имеют смысл. Покажем, что 1)  a·  b  0 ; 2) (  а ·  b) = ab .

2

Т.к. а  0, то  a  0; b  0 , то  b  0. Значит,  a ·  b  0 .

2

2

2

(  a ·  b ) = (  a) · (  b) = ab .

Значит,  ab =  a ·  b , где a  0, b  0.

 abc =  a ·  b ·  c , где a  0, b  0 , с  0.

Корень из произведения неотрицательных множителей равен произведению корней из этих множителей.

Как найти квадратный корень из дроби?????

Теорема 2. Если a  0 и b  0 , то 

a

 a

=

b

 b

Доказательство:

 a

 0 .

Так как a  0 , то  a  0 , т.к. b  0 , то  b  0 . Значит,

 b

 a

2

(  a)

2

a

( )

=

=

2

(  b)

b .

 b

a

 a



=

, где a  0 , b  0 .

Значит,

b

 b

Корень из дроби, числитель которой неотрицателен, а знаменатель положителен, равен корню из числителя, деленному на корень из знаменателя.

Рассмотрим примеры:

 64 · 0,04 =

 64 ·  0,04=

8 · 0,2 =

1,6 ;

 32 · 98 =

 ( 16 · 2) · (49 · 2 ) =

=  16 · 49 · 4=

4 · 7 · 2=

56;

 16 ·  49 ·  4 =

36

 36



6

=

=

121

 121

11

Стр. 82 № 369(а, в, д) № 370(а, в, д, е) № 372(а, в, г)

Домашнее задание:

п.15, № 371, 373.