Лабораторная работа №6 «Определение площадей с помощью интеграла»
Цель работы: Применение определённого интеграла для вычисления площадей фигур.
Теоретические сведения к лабораторной работе:
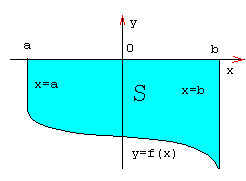
Фигура, изображённая на рисунке является криволинейной трапецией
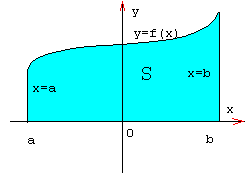
Определение
Криволинейной трапецией называется фигура, ограниченная сверху графиком непрерывной функции y=f(x), снизу отрезком [a;b] оси Ох, а с боков отрезками прямых х=а, х=b
Площадь криволинейной трапеции можно вычислить с помощью определённого интеграла
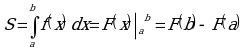
В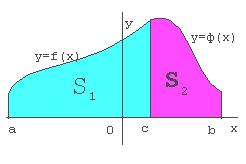 озможно такое расположение:
озможно такое расположение:
S = S1 +S2
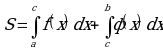
Возможен следующий случай, когда f(x)b]
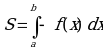
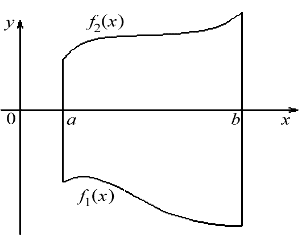
Возможно и такое расположение
 S=
S=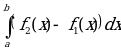
Задачи на вычисление площадей плоских фигур можно решать по следующему плану:
-
по условию задачи делают схематический чертёж;
-
представляют искомую фигуру как сумму или разность площадей криволинейных трапеций. Из условия задачи и чертежа определяют пределы интегрирования для каждой составляющей криволинейной трапеции.
-
записывают каждую функцию в виде 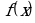
-
вычисляют площадь каждой криволинейной трапеции и искомой фигуры.
Пример
Найти площадь фигуры, ограниченной линиями.
S = 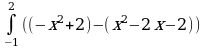 dx =
dx =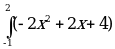 dx =
dx =
= (-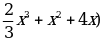 |
|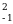 =-
=- 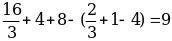 (кв. ед.)
(кв. ед.)
Задания для самостоятельного решения:
Найти площадь фигуры, ограниченной линиями
а) параболой у = (х + 1)2 , прямой у = 1 – х и осью Ох.
б) параболой у = х2 – 4х +3 и осью Ох.
в) графиком функции у = sinx , и отрезком [ π ; 2π] оси Ох.
а) параболой у = х2 + 4х - 3 и осью Ох.
б) параболой у = х2 + 1 и прямой у = 3 - х .
в) параболой у = -х2 и прямой у = - 4 .
Контрольные вопросы:
1. Что такое криволинейная трапеция?
2. Как вычислить площадь криволинейной трапеции?
3. По какому плану можно найти площадь любой плоской фигуры используя интеграл?








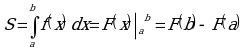
 озможно такое расположение:
озможно такое расположение: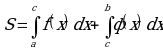

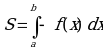
 S=
S=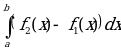

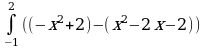 dx =
dx =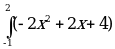 dx =
dx =


















