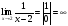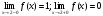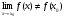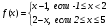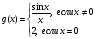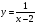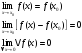Просмотр содержимого документа
«Лекция "Непрерывность функции"»
Непрерывность функции
1. Непрерывность функции в точке.
1 Определение: Функция f(x) называется непрерывной в точке х0, принадлежащей области определения функции, если для любого положительного числа ε существует такое положительное δ, что для всех х, удовлетворяющих условию 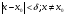 , будет выполнено неравенство
, будет выполнено неравенство 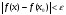
2 Определение: Пусть функция у=ƒ(х) определена в точке хо и в некоторой окрестности этой точки. Функция y=f(x) называется непрерывной в точке х0, если существует предел функции в этой точке и он равен значению функции в этой точке, т.е. 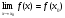 . Равенство означает выполнение трех условий:
. Равенство означает выполнение трех условий:
1) функция ƒ (х) определена в точке x0 и в ее окрестности;
2) функция ƒ(х) имеет предел при х→хо;
3) предел функции в точке хо равен значению функции в этой точке.
Условие непрерывности функции в точке: если односторонние пределы функции в точке х0 существуют и равны между собой, то существует предел функции в точке х0, следовательно, функция в точке х0 будет непрерывна.
Точки, в которых нарушается непрерывность функции, называются точками разрыва этой функции. Если х=х0 — точка разрыва функции у=ƒ(х), то в ней не выполняется по крайней мере одно из условий первого определения непрерывности функции, а именно:
| Случаи появления разрывов | Рисунок |
|
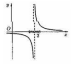
1. Функция определена в окрестности точки х0, но не определена в самой точке х0. 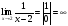
| 
|
|
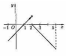
2. Функция определена в точке х0 и ее окрестности, но не существует предела ƒ(х) при х→х0. 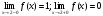
| 
|
|
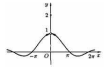
3. Функция определена в точке х0 и ее окрестности, предел функции в точке х0 существует, но этот предел не равен значению функции в точке x0. 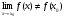
| 
|
2. Точки разрыва. Все точки разрыва функции разделяются на точки разрыва первого и второго рода.
- Точка разрыва х0 называется точкой разрыва первого рода функции у=ƒ(х), если в этой точке односторонние пределы существуют, конечны и не равны. График функции в этой точке претерпевает «скачок» равный разности между правым и левым пределом функции в этой точке.
- Точка разрыва х0 называется точкой разрыва второго рода функции у=ƒ(х), если по крайней мере один из односторонних пределов (слева или справа) не существует или равен бесконечности. График функции в этой точке устремляется в бесконечность.
| пример | Вид разрыва | Рисунок |
|
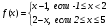
|
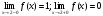
точка х0 =2 называется точкой конечного разрыва
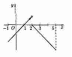
| 
|
|
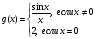
| 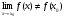
точка х0=0 называется точкой устранимого разрыва. Положив g(х)=1 (вместо g(х)=2) при х=0, разрыв устранится, функция станет непрерывной | 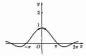
|
| 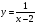
| 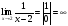
x0=2 -точка разрыва второго рода. | 
|
3. Непрерывность функции через приращения функции и аргумента.
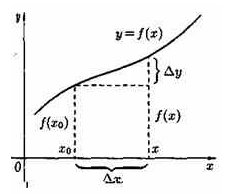
Пусть функция у=ƒ(х) определена в некотором интервале (а;b). Возьмем произвольную точку хоє(а;b). Для любого хє(а;b) разность х-хо называется приращением аргумента х в точке х0 и обозначается ∆х («дельта х»): ∆х=х-x0. Отсюда х=х0+∆х.
Разность соответствующих значений функций ƒ(х)-ƒ(х0) называется приращением функции ƒ(х) в точке х0 и обозначается ∆у (или ∆ƒ или ∆ƒ(х0)): ∆у=ƒ(х)-ƒ(х0) или ∆у=ƒ(х0+∆х)-ƒ(х0)
3 Определение: Функция f(x) называется непрерывной в точке х0, если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.
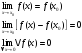







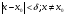 , будет выполнено неравенство
, будет выполнено неравенство 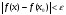
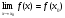 . Равенство означает выполнение трех условий:
. Равенство означает выполнение трех условий: