

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 14.06.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

Была в сети 04.10.2022 17:18

Водяхина Наталья Владимировна
Преподаватель математики
Местоположение
Россия, Балаково
Специализация
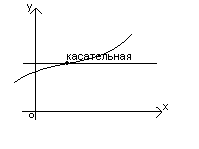
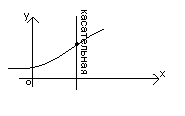
Лекция по теме геометрический и физический смысл производной
Категория:
Математика
28.10.2021 08:10


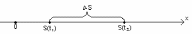
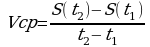 или
или 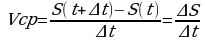
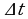
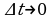
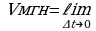
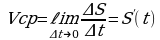

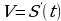
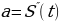 ,
,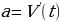 или
или - производная второго порядка функции S(t).
- производная второго порядка функции S(t). изический (механический) смысл производной второго порядка состоит в том, что если S(t)-закон линейного движения тела, то производная второго порядка выражает ускорение в момент времени t.
изический (механический) смысл производной второго порядка состоит в том, что если S(t)-закон линейного движения тела, то производная второго порядка выражает ускорение в момент времени t.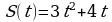 . Найдите скорость точки в момент времени t=2с.
. Найдите скорость точки в момент времени t=2с.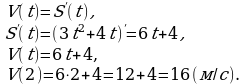
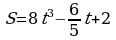 . Найдите ускорение точки в конце второй секунды.
. Найдите ускорение точки в конце второй секунды.
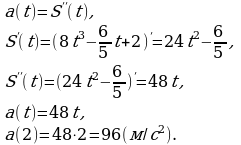
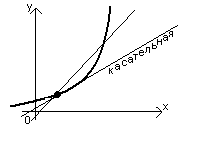
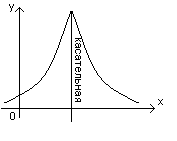
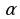

 y=f(x)
y=f(x)
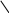


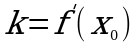
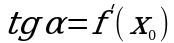
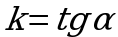
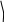

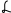
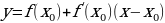

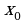 .
.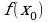 .
.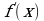 .
.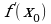 .
.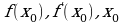 в формулу.
в формулу.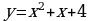 в точке с абсциссой х = 1.
в точке с абсциссой х = 1.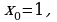
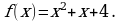
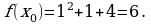
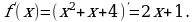
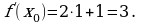
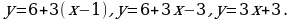
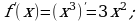
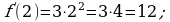
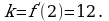
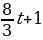 1. Скорость
1. Скорость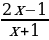
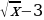
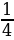
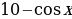
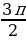
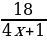
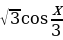
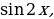
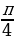
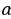
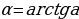

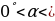
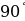
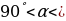
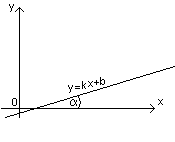
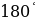 1.Угловой коэффициент касательной
1.Угловой коэффициент касательной

















