Экстремумы функций

Экстремумы функции

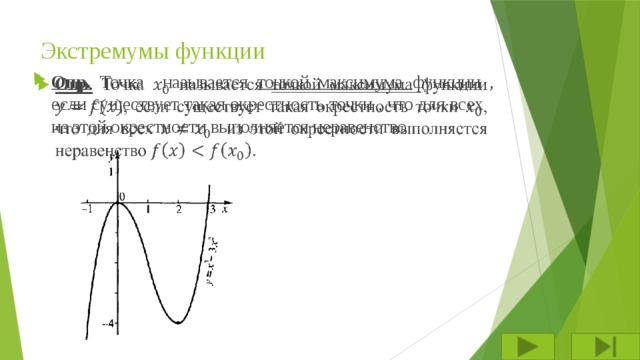
• Опр. Точка называется точкой максимума функции , если существует такая окрестность точки , что для всех из этой окрестности выполняется неравенство

Опр . Точка называется точкой минимума функции , если существует такая окрестность точки , что для всех из этой окрестности выполняется неравенство

Точки минимума и точки максимума называются точками экстремума функции.

Теорема. Если точка экстремума дифференцируемой функции , то .

Геометрический смысл: в точке экстремума касательная параллельна оси абсцисс и поэтому ее угловой коэффициент равен нулю.

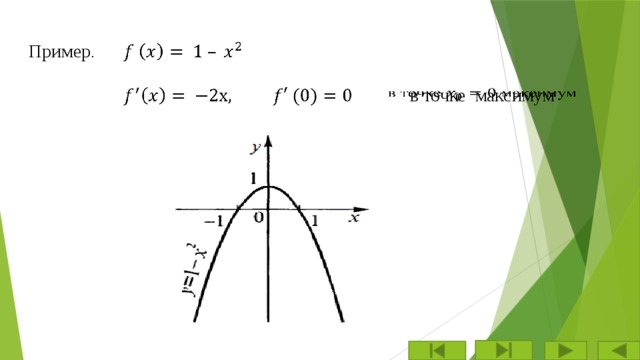
Пример .

в точке максимум

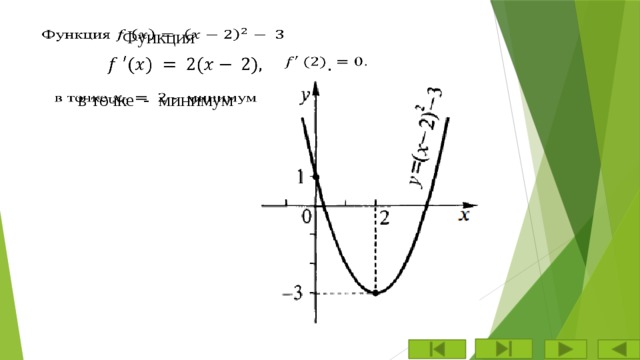
Функция

.

в точке - минимум

Точки, в которых производная функции обращается в нуль, называют стационарными.

Уравнение может иметь корни, которые не являются точками экстремума функции .

– стационарная точка

Но не является точкой экстремума!

3адача 1. Найти стационарные точки функции

стационарные точки являются корнями квадратного уравнения

– стационарные точки функции

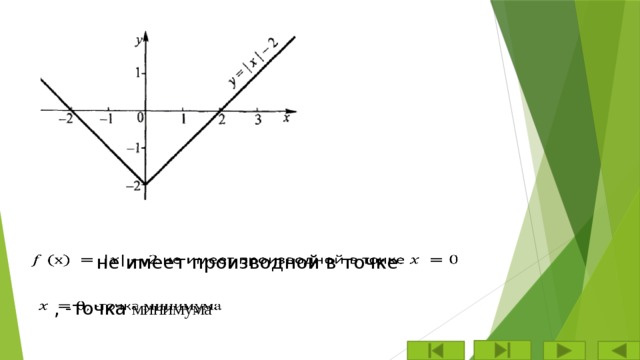
не имеет производной в точке

, -точка минимума

Внутренняя точка области определения функции, в которой эта функция имеет производную, равную нулю , или не имеет производной, называется критической точкой этой функции.

Для того чтобы точка была точкой экстремума функции , необходимо , чтобы эта точка была критической для данной функции.

Достаточные условия экстремума

Теорема 2.

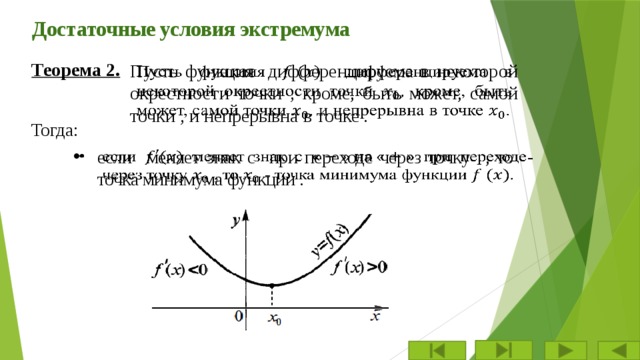
Пусть функция дифференцируема в некоторой окрестности точки , кроме, быть может, самой точки , и непрерывна в точке .

Тогда:

• если меняет знак с при переходе через точку , то - точка минимума функции .

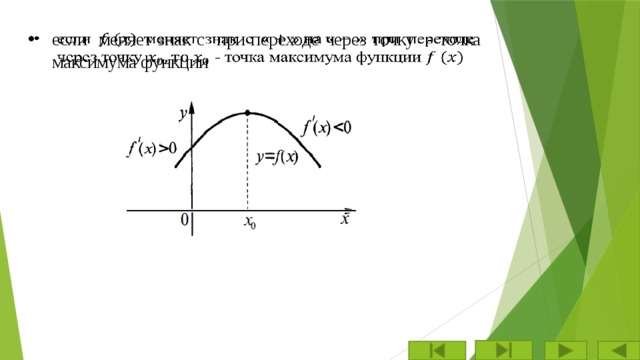
• если меняет знак с при переходе через точку - точка максимума функции

3адача 2. Найти точки экстремума функции

Решение.

При переходе через точку производная меняет знак с .

При переходе через точку производная меняет знак с,

- точка максимума

- точка минимума .

Упражнения.

100. Найти стационарные точки функции:

3) ;

1)

5

7

Найти точки экстремума функции ( 102-103).

3)

102. 1

5)

7 ) ;

;

Задание на дом :

Колягин Ю.М. (2010). АЛГЕБРА И НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА . Москва: Мнемозина.

§ 8. Экстремумы функции

№№ 100 (2, 4, 6, 8); 101(2, 4);102 (2, 4, 6, 8)