11 класс. Объем шара и площадь сферы.

КОУ ВО «ЦЛПДО»

Разработка уроков-консультаций в 11 классе.

«Объем шара и площадь сферы».

Подготовила

Л.И. Гоптарь.

-Воронеж-

2020 г.

Цель и задачи урока:

продолжить систематическое изучение тел вращения в ходе решения базовых задач на вычисление их объемов.

Теоретический материал ( вспоминаем определения ).

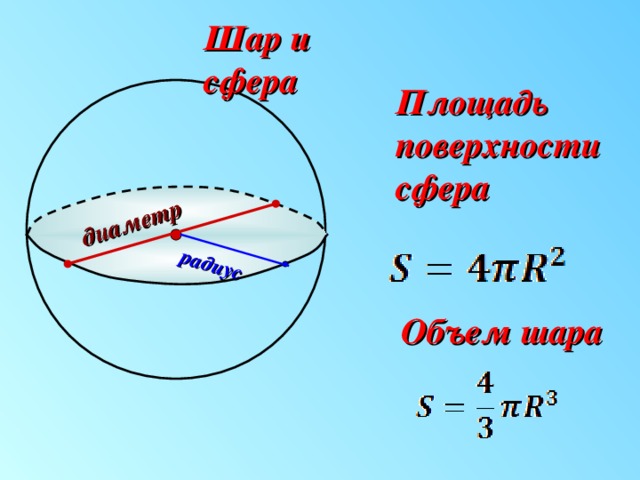
Шаром называется множество всех точек пространства, находящихся от данной точки на расстоянии, не больше данного R.

Радиусом шара называют всякий отрезок, соединяющий центр шара с точкой шаровой поверхности.

Отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара, называется диаметром шара.

Концы любого диаметра шара называются диаметрально противоположными точками шара.

Отрезок, соединяющий две любые точки шаровой поверхности и не являющийся диаметром шара, называют хордой шара.

 Сферическим поясом (шаровым поясом) называют часть сферы, заключенную между двумя параллельными плоскостями .

 Шаровым слоем называют часть шара, заключенную между двумя параллельными плоскостями .

Сферическим сегментом называют каждую из двух частей, на которые делит сферу пересекающая ее плоскость.

Шаровым сегментом называется часть шара, отсекаемая от него какой-нибудь плоскостью.

Шаровым сектором называют фигуру, состоящую из всех отрезков, соединяющих точки сферического сегмента с центром сферы.

Объем шара равен  .

Объем шарового сегмента равен  .

Объем шарового сектора равен  .

Объем шарового слоя равен  .

Площадь сферы равна S=4 πR².

Примеры и разбор решения заданий тренировочного модуля

№1. Круговой сектор радиуса R с центральным углом 60 градусов вращается вокруг одного из радиусов, образующих этот угол. Найдите объем тела вращения. 

Решение:

При вращении кругового сектора АОВ вокруг радиуса ОА получается тело вращения - шаровой сектор радиуса R=ОА и высотой сектора h=DA.

Объем его вычисляется по формуле: V= (2/3)*πR²*h.

 Рассмотрим сечение этого сектора (смотри рисунок): в прямоугольном треугольнике ОВD (радиус круга ОА перпендикулярен хорде ВС) угол ВОD равен 60° (дано).

Значит:

Тогда высота шарового сектора равна h=DA=OA-OD=R-R/2=R/2. 
V=(2/3)*π*R²*R/2=(1/3)πR³. 

№2. Найдите объем шарового сектора, если радиус шара равен 6 см, а высота конуса, образующего сектор, составляет треть диаметра шара.

Решение:

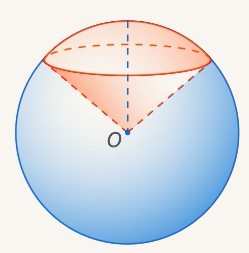
Шаровой сектор — это часть шара, ограниченная кривой поверхностью шарового сегмента и конической поверхностью, основанием которой служит основание сегмента, а вершиной — центр шара.

 Формула объема шарового сектора: V = (2/3)*πR²*h, где h - высота сегмента.

В нашем случае  R=H+h, где Н - высота конуса, а h- высота сегмента.

Тогда h = R-H = 6-4 =2, так как Н = (1/3)*2*R (дано).

Значит V = (2/3)*π*36*2 = 48π.

Ответ: объем шарового сектора равен 48π

№3.По разные стороны от центра шара проведены два параллельных сечения с площадью   и   см².

Расстояние между сечениями равно   см.

Определите объём получившегося шарового слоя.

Решение: запишем формулу для вычисления объема шарового слоя.

Чтобы найти объём шарового слоя нам необходимо знать его высоту и радиусы двух его оснований.

По условию задачи нам дано расстояние между сечениями, как раз-таки это расстояние и есть высота данного шарового слоя, и она равна  .

Теперь найдём чему равны радиусы оснований шарового слоя. Напомню, что сечением шара плоскостью является круг. Площадь круга вычисляется по формуле  .

Отсюда найдём радиусы оснований шарового слоя. Тогда имеем, радиус одного основания равен   (см), радиус второго основания равен   (см).

Подставим радиусы оснований и высоту шарового слоя в формулу его объёма.

Посчитаем. Получаем, что объём данного шарового слоя равен 

Итог урока. Оценки.