Арифметическая и геометрическая прогрессии

Арифметическая и геометрическая прогрессии.

Вариант №1.

А1. Найдите шестой член арифметической прогрессии: -7; -3;

1)11 2)12 3)13 4)14

А2. Найдите пятый член геометрической прогрессии: 81; -27;

1)3 2)-3 3)-1 4)1

А3. Сумма третьего, восьмого и девятнадцатого члена арифметической прогрессии равна 72. Найдите десятый член этой прогрессии.

1)18 2)27 3)24 4)36

А4. В геометрической прогрессии . Найдите .

1) 2) 3) 4)

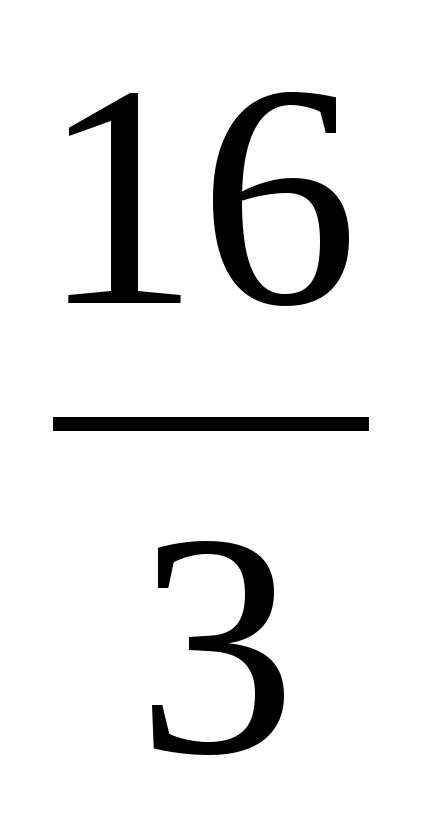
А5. В арифметической прогрессии известно, что . Найдите сумму шести первых членов.

1)57 2)57,5 3)58 4)58,5

А6. В геометрической прогрессии известно, что Найдите .

1)96 2)-96 3)48 4)-48

В1. Третий член арифметической прогрессии равен -6, сумма второго и пятого членов равна -9. Известно, что один из членов прогрессии равен 15. Найдите его номер.

В2. При подготовке к экзамену ученик каждый день увеличивал количество решенных задач на одно и тоже число. С 3 мая по 6 мая включительно он решил 24 задачи, а с 5 мая по 10 мая -72 задачи. Сколько задач ученик решил с 3 по 10 мая включительно?

В3. Третий член геометрической прогрессии равен 2. Чему равно произведение первых ее пяти членов?

С1. Четыре числа образуют арифметическую прогрессию. Если к этим числам прибавить соответственно 1,2,11,44, то получим четыре числа, образующих геометрическую прогрессию. Найдите числа, образующие арифметическую прогрессию.

Вариант №2.

А1. Найдите седьмой член арифметической прогрессии: 13; 0; …

1)-9 2)-7 3)-5 4)-3

А2. Найдите шестой член геометрической прогрессии:96; -48; …

А3. Сумма второго, девятого и десятого члена арифметической прогрессии равна 60. Найдите седьмой член этой прогрессии.

1)15 2)20 3)30 4)45

А4. В геометрической прогрессии . Найдите .

1) 2) 3) 4)

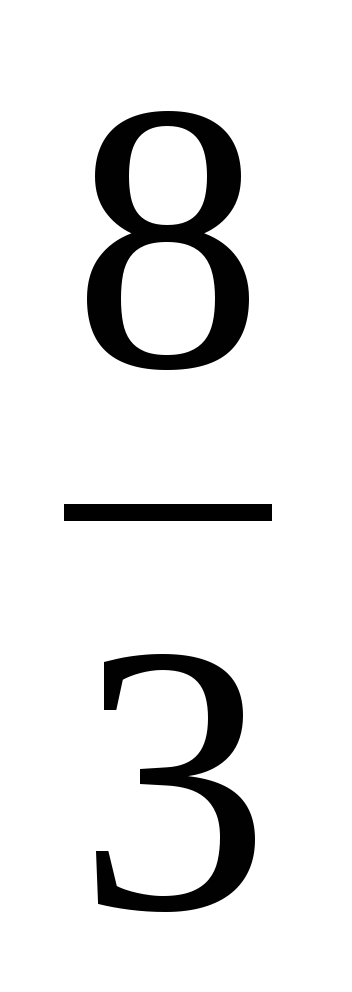
А5. В арифметической прогрессии известно, что . Найдите сумму пяти первых членов.

1)47 2)47,5 3)48 4)48,5

А6. В геометрической прогрессии известно, что Найдите .

1)256 2)-256 3)128 4)-128

В1. Второй член арифметической прогрессии равен -7, разность пятого и восьмого членов равна -6. Известно, что один из членов прогрессии равен 9. Найдите его номер.

В2. При подготовке к экзамену ученик каждый день с 1 по 8 июня включительно увеличивал количество решенных задач на одно и тоже число. С 1 июня по 4 июня включительно он решил 24 задачи, а с 2июня по 6 июня -45 задач. Сколько задач ученик решил 8 июня?

В3. Четвертый член геометрической прогрессии равен -2. Чему равно произведение первых ее семи членов?

С1. Четыре числа образуют геометрическую прогрессию. Если к этим числам прибавить соответственно 2,5,7,7, то получим четыре числа, образующих арифметическую прогрессию. Найдите числа, образующие геометрическую прогрессию.