

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

Была в сети 30.11.2020 08:49

Чудутова Вера Убушаевна
учитель математики (надомное обучение)
64 года
Местоположение
Россия, Элиста
Дидактический материал для учащихся с ОВЗ по математике 9 класс
Категория:
Математика
13.04.2016 13:33


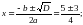
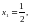 x2 = 2. Значит,
x2 = 2. Значит,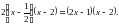
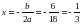 .
. 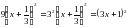 .
. ;
;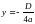 или по формуле у0 = ах02 + bx0 + c ;
или по формуле у0 = ах02 + bx0 + c ; 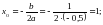




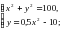



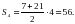

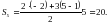
 .
.

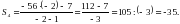
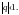 У неё ( при бесконечном увеличении числа членов)
У неё ( при бесконечном увеличении числа членов)  , называемому суммой прогрессии и вычисляется по формуле:
, называемому суммой прогрессии и вычисляется по формуле: 









