ФОНД ОЦЕНОЧНЫХ СРЕДСТВ ПО УЧЕБНОМУ ПРЕДМЕТУ «ГЕОМЕТРИЯ»
для учащихся 10-11 классов
10 класс.
Зачетное занятие 1 полугодие.
В каком случае три точки в пространстве не определяют положение плокости, проходящей через эти точки?
Могут ли две различные плоскости иметь только две общие точки?
Что можно сказать о взаимном положении двух плоскостей, имеющих три общие точки, не лежащие на одной прямой?
Точка М не лежит на прямой а. Через точку М проводятся прямые, пересекающие прямую а. Лежат ли эти прямые в одной плоскости?
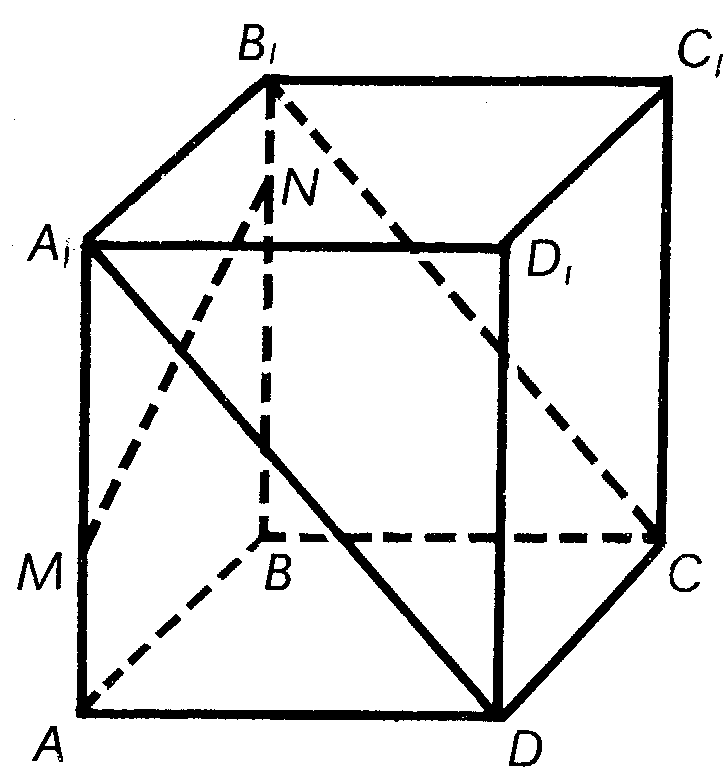
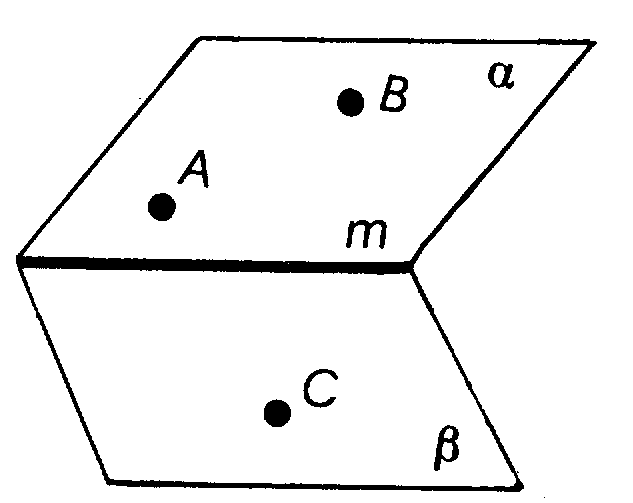
Каково взаимное положение прямых (рис 1): A1D и MN; A1D и B1C; MN и A1B1 ?
Рис 1
Рис 2
Рис 3
Рис 4
Прямые а и b скрещиваются с прямой с. 1) Могут ли прямые а и b пересекаться?
2) Могут ли прямые а и b быть параллельными?
Прямая а параллельна плоскости . Существуют ли на плоскости прямые, не параллельные прямой a? Если да, то каково их взаимное положение?
Две прямые параллельны одной и той же плоскости. Можно ли утверждать, что эти прямые параллельны между собой? Если нет, то каково их взаимное положение?
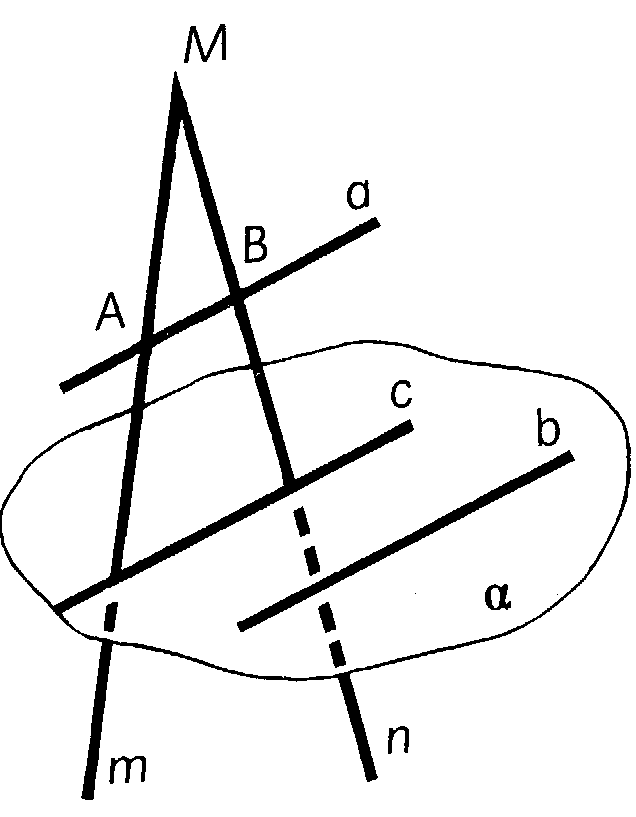
Прямые m и n пересекаются в точке М (рис 2). Точка А лежит на прямой m, точка В лежит на прямой n, прямая b лежит в плоскости , прямые а и b параллельны. Каково взаимное положение прямых b и c?
Прямые а и b лежат в пересекающихся плоскостях и . Могут ли эти прямые быть: 1) параллельными; 2) скрещивающимися?
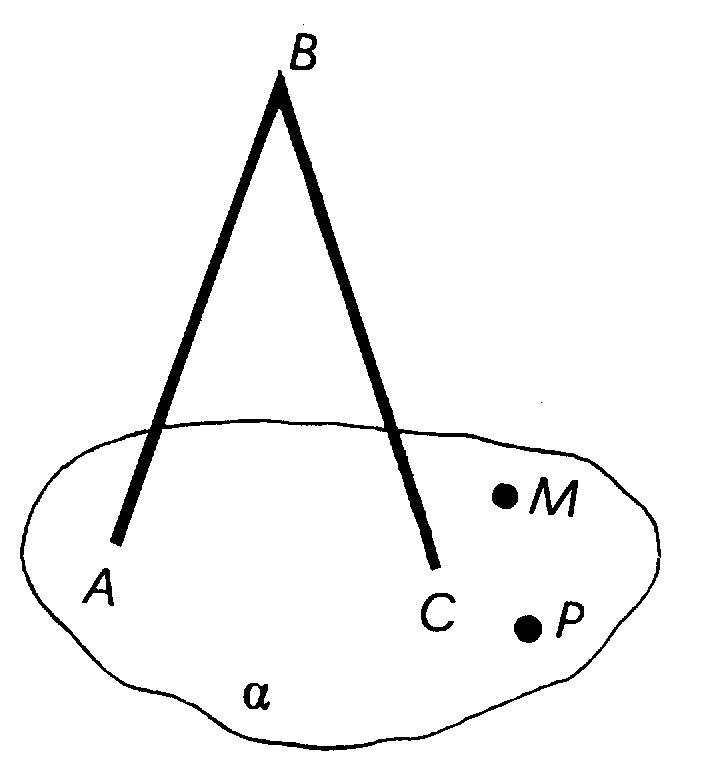
Точки A, С, M и P лежат в плоскости , а точка B не лежит в плоскости (рис 3). Постройте точку пересечения прямой MP с плоскостью ABC.
Точки A и B лежат в плоскости , а точка С лежит в плоскости (рис 4). Постройте линии пересечения плоскости ABC с плоскостями и .
Прямая а параллельна плоскости . Прямые b и c, пересекающие прямую а, пересекают плоскость соответственно в точках B и С. Каким может быть взаимное положение прямых b и c ?
Плоскости и пересекаются по прямой m, прямая а лежит в плоскости . Каково возможное взаимное положение прямой а и плоскости ?
Прямая а параллельна плоскости , точка М и прямая с лежат в плоскости
(точка М не лежит на прямой с). Через точку М проведена прямая b, параллельная прямой а. Каково взаимное положение прямых b и c ?
Отрезок AB параллелен плоскости , отрезок CD лежит в плоскости , AB=CD. Можно ли утверждать, что четырёхугольник ABDC - параллелограмм?
Нормы оценок:
«2» 0-4
«3» 5-8
«4» 9-12
«5» 13-16
Контрольная работа «Прямые и плоскости в пространстве. Параллельность прямых и плоскостей»
1 вариант
При выполнении заданий А1-А3 укажите букву с верным ответом.
А 1.
а) Любые четыре точки лежат в одной плоскости;
б) Любые три точки не лежат в одной плоскости;
в) Любые четыре точки не лежат в одной плоскости;
г) Любые три различные точки не лежат в одной плоскости;
А 2.
Назовите общую прямую плоскостей РВМ и МАВ.
а) РМ; б) А В; в) РВ; г) ВМ.
А 3.
Через вершины параллелограмма, лежащего в одной из двух параллельных плоскостей, проведены параллельные прямые, пересекающие вторую плоскость в точках ,
, ,
,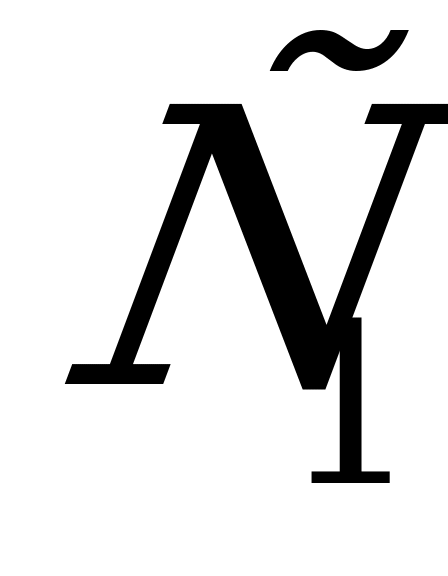 ,
,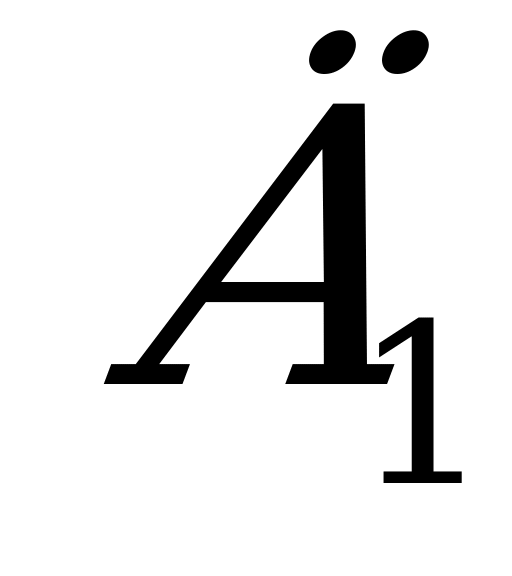 .Тогда
.Тогда 

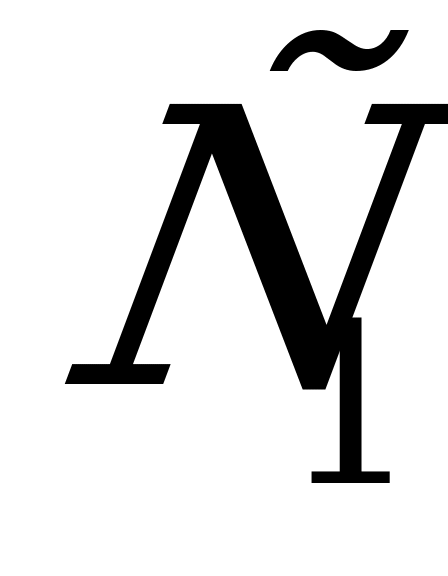
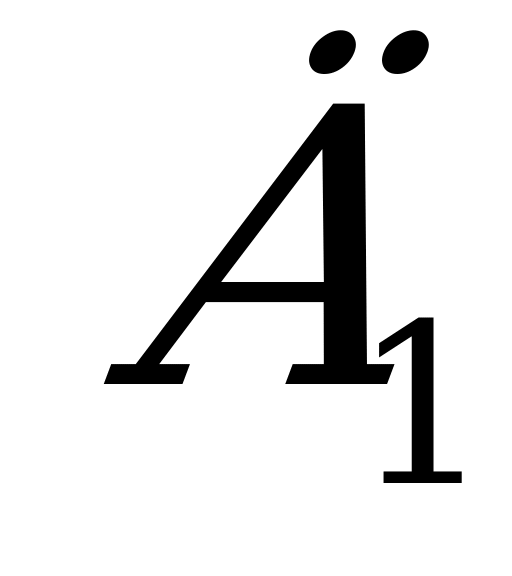 представляет собой:
представляет собой:
а) трапецию; б) ромб; в) параллелограмм; г) прямоугольник.
При выполнении задания В достаточно указать ответ.
В. Плоскость  пересекает стороны АВ и ВС треугольника АВС в точках Д и Е соответственно, причем АС параллельна плоскости
пересекает стороны АВ и ВС треугольника АВС в точках Д и Е соответственно, причем АС параллельна плоскости .
.
Найдите АС, если ВД: АД=3:4,ДЕ=10.
При выполнении задания С необходимо представить полное решение.
С. Сторона ромба MCDN равна 4 см, MNKP -параллелограмм. Найдите периметр четырехугольника CDKP , если NK=8см, 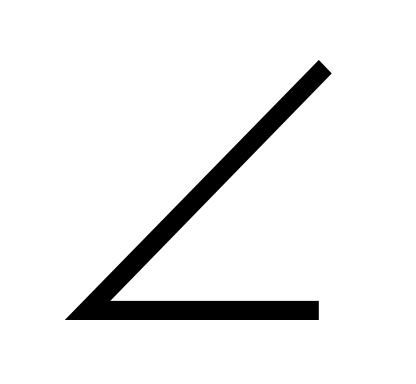 CMP=
CMP= .
.
2 вариант
При выполнении заданий А1-А3 укажите букву с верным ответом.
А 1.
а) Через любые три точки проходит плоскость и притом только одна;
б) Если две точки прямой лежат в одной плоскости, то и вся прямая лежит в этой плоскости;
в) Через прямую и точку, лежащую на не, проходит единственная плоскость;
г) Нельзя провести плоскость через две параллельные прямые.
А 2.
Назовите общую прямую плоскостей AFD и DEF.
а) AF; б) FD; в) AE; г) ED.
А 3.
Через концы отрезка AB,не пересекающего плоскость и точку C – его середину, проведены параллельные прямые, пересекающие плоскость
и точку C – его середину, проведены параллельные прямые, пересекающие плоскость
 ,
, ,
,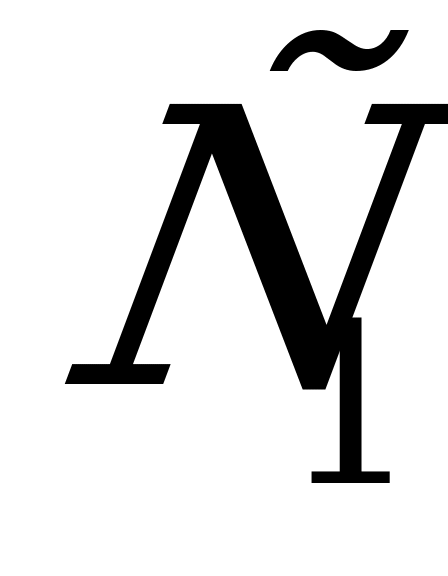 соответственно. Найдите
соответственно. Найдите 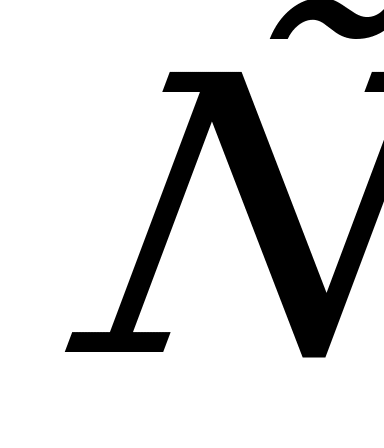
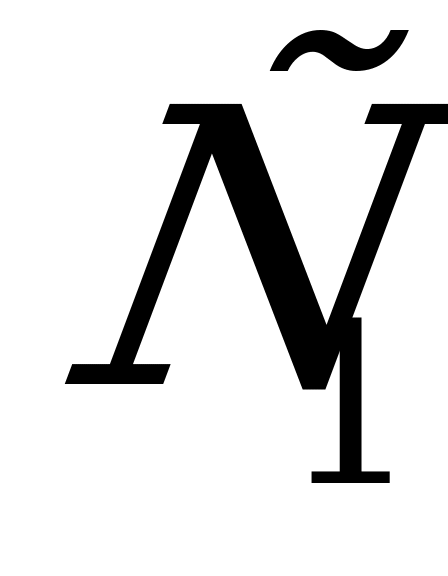 , если
, если =12,
=12,  =6.
=6.
а) 6; б) 9; в) 6 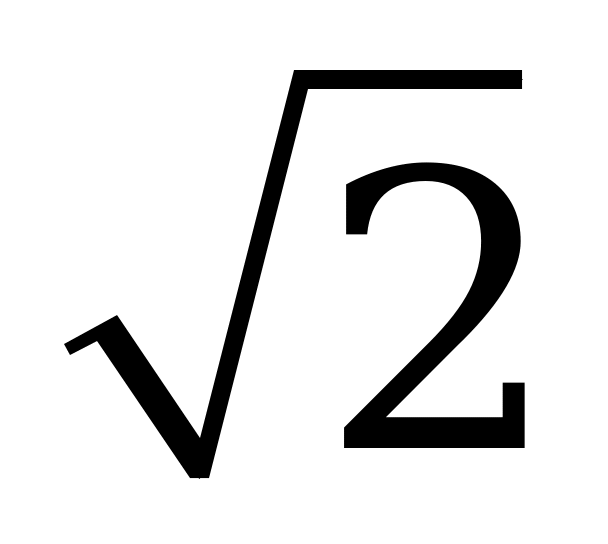 ; г) другой ответ.
; г) другой ответ.
При выполнении задания В. В достаточно указать ответ.
В. Плоскость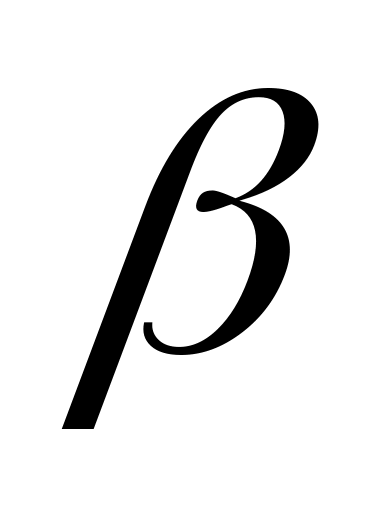 пересекает стороны MP и KP треугольника MPK соответственно в точках N и E, причем сторона MK параллельна плоскости
пересекает стороны MP и KP треугольника MPK соответственно в точках N и E, причем сторона MK параллельна плоскости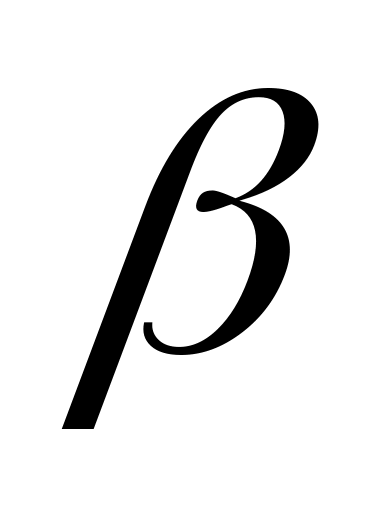 , MK=12, MN: NP=3:5.Найдите NE.
, MK=12, MN: NP=3:5.Найдите NE.
При выполнении задания С необходимо представить полное решение.
С. Сторона ромба CDEK равна 8 см, CKMN -параллелограмм. Найдите периметр четырехугольника DEMN , если KM =6см, 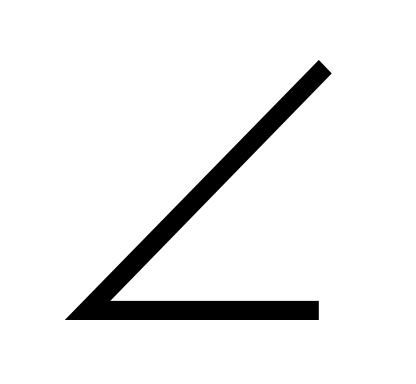 DCN=
DCN= .
.
Ответы.
1 вариант
| Задания | А 1 | А 2 | А3 | В | С |
| Ответы | г | г | в | 23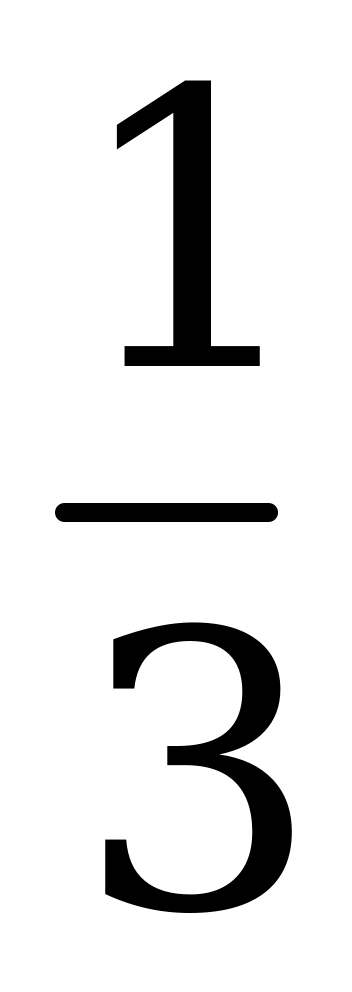 | 8+8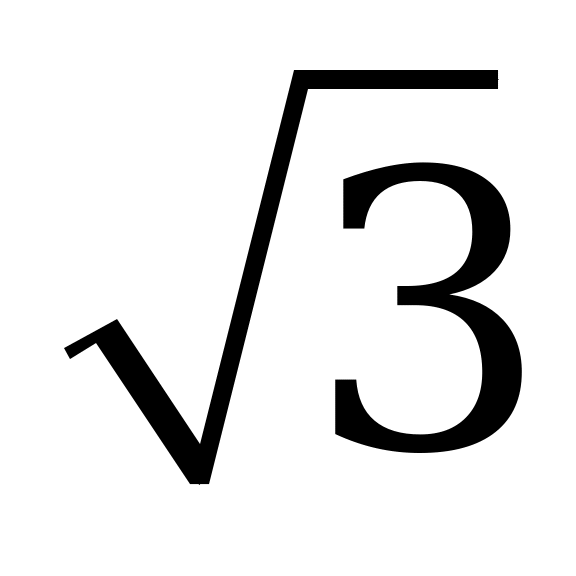 |
| Баллы | 1 | 1 | 1 | 2 | 3 |
2 вариант
| Задания | А 1 | А 2 | А3 | В | С |
| Ответы | б | б | б | 7,5 | 16+4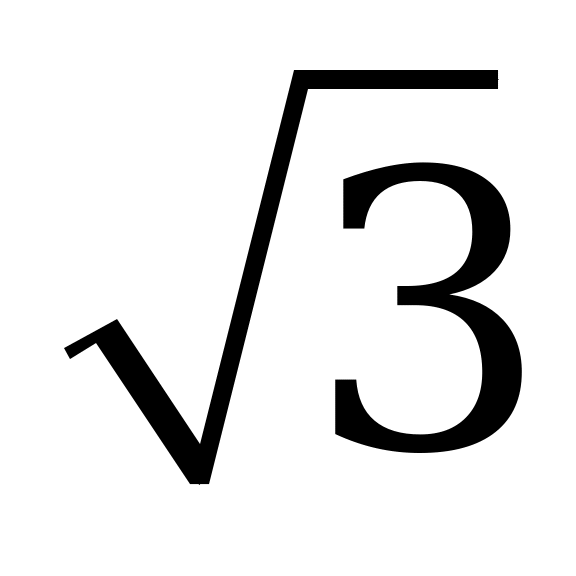 |
| Баллы | 1 | 1 | 1 | 2 | 3 |
Нормы оценок:
«2» 0-2
«3» 3-4
«4» 5-6
«5» 7-8
Контрольная работа «Перпендикулярность прямых и плоскостей».
1 вариант
При выполнении заданий А1-А3 укажите букву с верным ответом.
А 1. Две скрещивающиеся прямые взаимно перпендикулярны. Чему равен угол между ними:
а)  ; б)
; б) 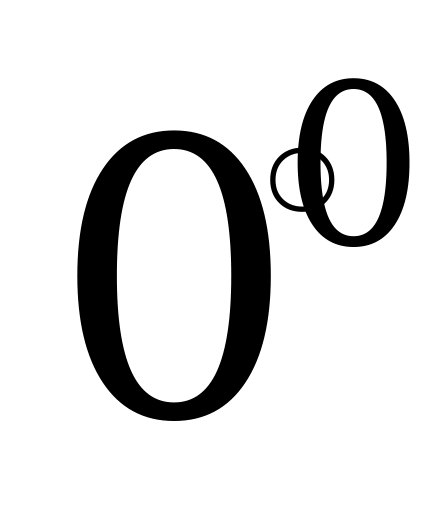 ; в)
; в) 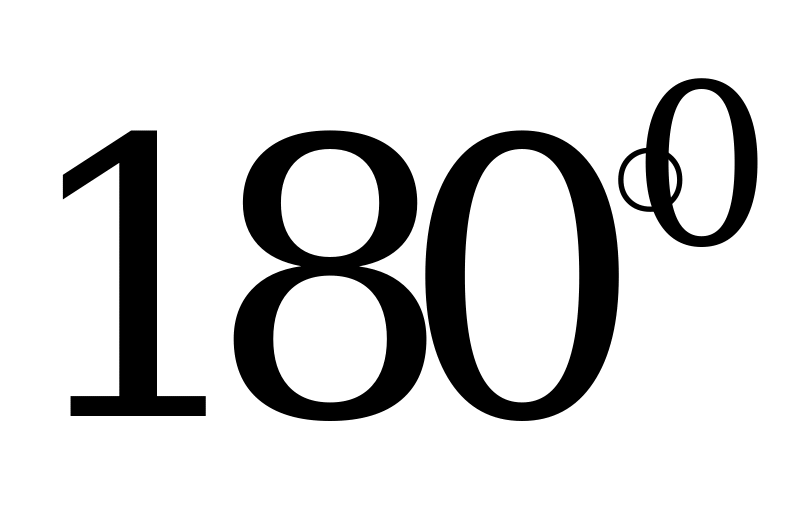 ; г) нельзя определить.
; г) нельзя определить.
А 2.Прямая перпендикулярна к двум различным плоскостям, тогда плоскости:
а) пересекаются; б) скрещиваются; в) параллельны; г) нельзя определить;
А 3.Прямая m перпендикулярна к прямым a и b,лежащим в плоскости  ,но m не перпендикулярна плоскости
,но m не перпендикулярна плоскости .Тогда прямые a и b:
.Тогда прямые a и b:
а) параллельны; б) пересекаются; в) скрещиваются; г) нельзя определить;
При выполнении задания В достаточно указать ответ.
В.Из точки к плоскости проведены две наклонные ,равные 23сми 33см .Найдите расстояние от этой точки до плоскости, если проекции наклонных как 2:3.
При выполнении задания С необходимо представить полное решение задачи.
С. Из вершины равностороннего треугольника АВС восстановлен перпендикуляр АД к плоскости треугольника. Найдите расстояние от точки Д до стороны ВС, если АД=13см, ВС=6см.
2 вариант
При выполнении заданий А1-А3 укажите букву с верным ответом.
А 1. Две прямые a и b параллельны, а прямые b и c перпендикулярны. Чему равен угол между a и c:
а) 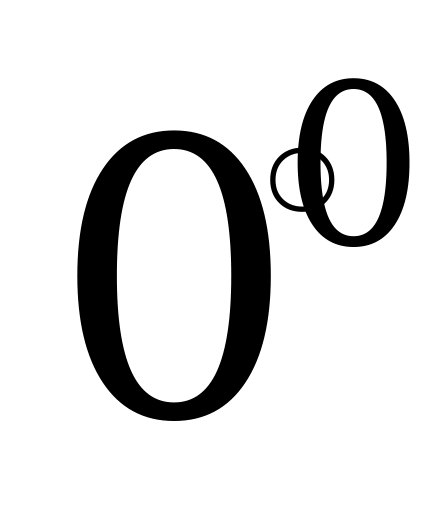 ; б)
; б) 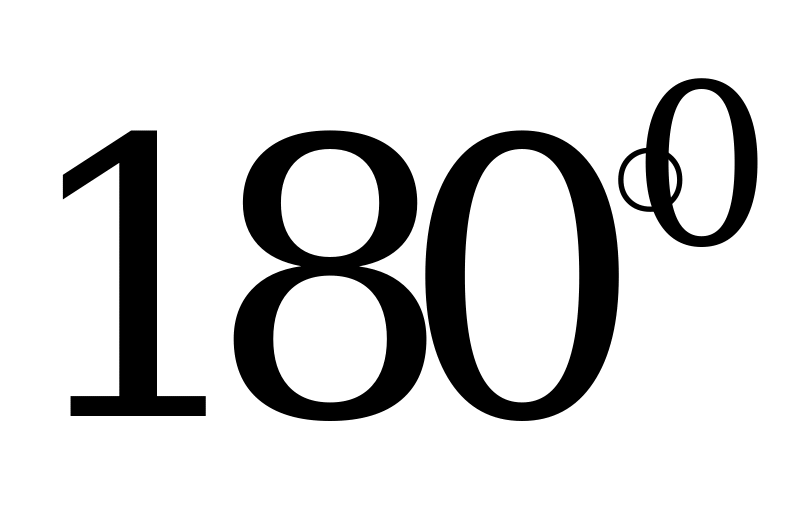 ; в)
; в)  ; г) нельзя определить.
; г) нельзя определить.
А 2.Две различныеплоскости перпендикулярны к некоторой прямой. Тогда эти плоскости:
а) перпендикулярны; б) параллельны; в) скрещиваются; г) нельзя определить;
А 3.Какое утверждение неверно:
а) перпендикуляр и наклонная, выходящие из одной точки имеют разные длины;
б) равные наклонные, проведенные из одной точки, имеют равные проекции;
в) Из двух наклонных проведенных из одной точки больше та проекция, которой больше;
г) Любая наклонная не больше своей проекции;
При выполнении задания В достаточно указать ответ.
В.Из точки к плоскости проведены две наклонные. Найти произведение их длин, если наклонные относятся как 1:2,а их проекции равны 1см и 7 см.
При выполнении задания С необходимо представить полное решение задачи.
Расстояние от данной точки до плоскости треугольника равно1,1м,а до каждой из вершин треугольника-6,1м. Найти радиус окружности, вписанной в этот треугольник.
Ответы.
1 вариант
| Задания | А 1 | А 2 | А3 | В | С |
| Ответы | а | в | а | 9см | 14см |
| Баллы | 1 | 1 | 1 | 2 | 3 |
2 вариант
| Задания | А 1 | А 2 | А3 | В | С |
| Ответы | в | б | г | 32 | 6 |
| Баллы | 1 | 1 | 1 | 2 | 3 |
Зачетное занятие по теме: «Перпендикулярность прямых и плоскостей».
Вариант 1.
1. Какое из следующих утверждений верно?
а) Две прямые перпендикулярные третьей перпендикулярны между собой;
б) прямая называется перпендикулярной плоскости, если она перпендикулярна хотя бы одной прямой, лежащей в этой плоскости;
в) две прямые, перпендикулярные к плоскости, перпендикулярны между собой;
г) прямая называется перпендикулярной плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.
Ответ обосновать.
2. Расстояние от точки М до каждой из вершин правильного треугольника ABCравно 4см(рис. 2). Найдите расстояние от точки Mдо плоскости ABC, если AB = 6см.
 Рис.2 М
Рис.2 М
А В
О
С
3. Плоскости  и
и 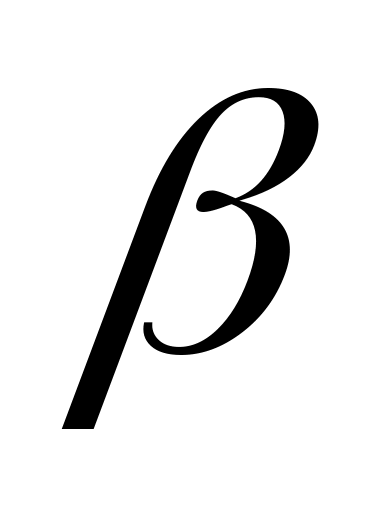 пересекаются по прямой с. Точка, лежащая в плоскости
пересекаются по прямой с. Точка, лежащая в плоскости  , удалена от плоскости
, удалена от плоскости 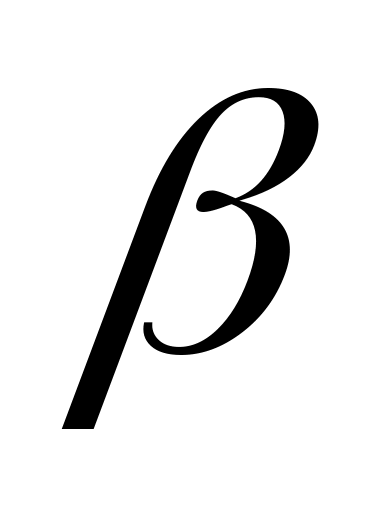 на
на 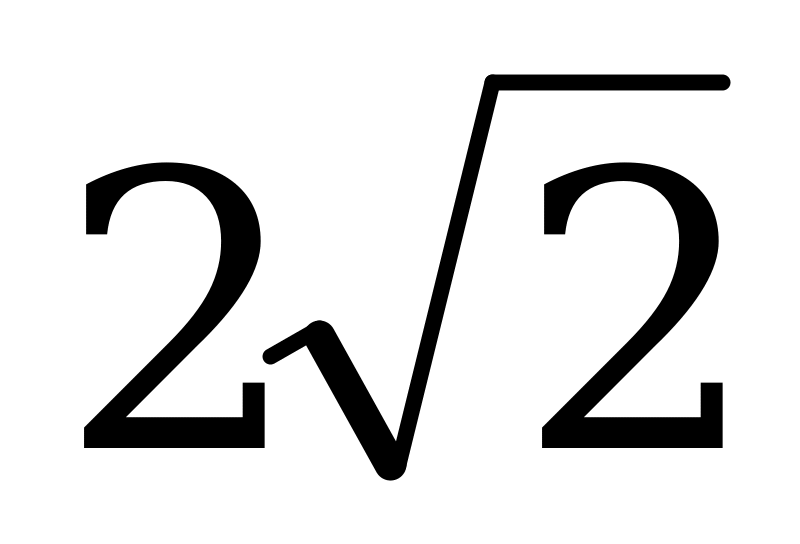 см, а от прямой с – на 4см. Найти угол между
см, а от прямой с – на 4см. Найти угол между и
и 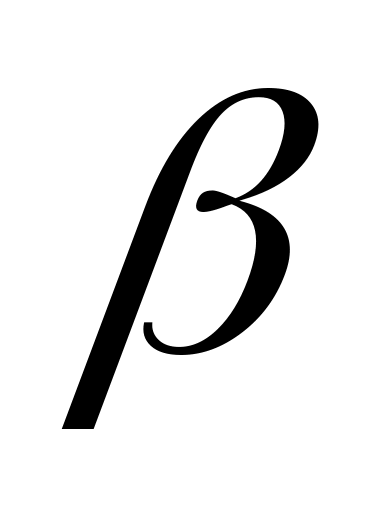 .
.
4. АВСДА1В1С1Д1 прямоугольный параллелепипед в основании которого лежит квадрат АВСД . Боковая грань АА1В1В и диагональное сечение ВВ1Д1Д образуют угол равный а) ) 300; б) 450; в) 600; г) 1350.
Ответ обосновать.
Вариант 2.
1. Две скрещивающиеся прямые взаимно перпендикулярны. Чему равен угол между ними?
а) 900; б) 00; в) 1800; г) 450.
Ответ обосновать.
Отрезок КА – перпендикуляр к плоскости квадрата АВСД, площадь которого 36 см2 (рис. 3). Найти расстояние между прямыми КА и ВС.
а) 6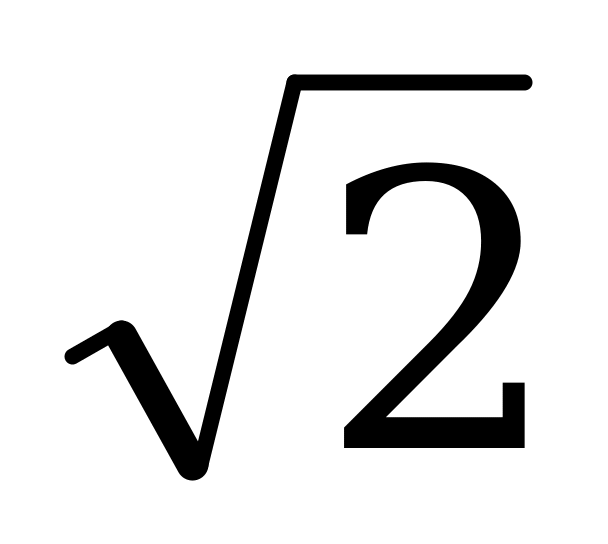 см; б) 12 см; в) определить нельзя, не хватает данных; г) 6 см.
см; б) 12 см; в) определить нельзя, не хватает данных; г) 6 см.

К
Рис. 3
А В
Д С
Прямая ДА перпендикулярна сторонам АВ и АС треугольника АВС и не лежит в его плоскости (рис. 1). Перпендикулярными являются плоскости
а) ДАС и АВС; б) ДАВ и ДВС; в) ДАС и ДВС; г) ДВС и АВС.
 Д Рис. 1
Д Рис. 1
С А
В
Ответ обосновать.
4. Через точку А, удаленную от плоскости α на 4см, проходит прямая, пересекающая плоскость α в точке В. Найдите угол между прямой АВ и плоскостью α, если длина отрезка АВ равна 6см.
а) arccos2/3; б) arcsin2/3; в) arcsin3/2; г) arctg2/3.
Нормы оценок:
«2» 0-1
«3» 2
«4» 3
«5» 4
11 класс.
Зачетное занятие.
Вариант 1.
ЧАСТЬ А.
Какие из утверждений верны:
А) Прямая перпендикулярна плоскости, если она перпендикулярна прямой, лежащей в этой плоскости.
Б) Длина перпендикуляра, опущенного из данной точки на плоскость, называется расстоянием от данной точки до плоскости.
В) Если к плоскости проведены две наклонные, то их проекции на плоскость равны.
Г) Если прямая, параллельна плоскости, то все её точки находятся на одинаковом расстоянии от этой плоскости.
Справедливы ли утверждения:
А) АВСД- параллелограмм, АК�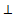 � АВ, значит ДС�
� АВ, значит ДС�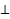 � АК.
� АК.
Б) АВСД –квадрат, ВР �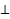 � (АВС), значит треугольник РСД – прямоугольный.
� (АВС), значит треугольник РСД – прямоугольный.
В) АВСД – ромб, ВД�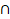 �АС=О, ОЕ�
�АС=О, ОЕ�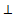 � ВД, значит ОЕ�
� ВД, значит ОЕ�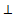 � АС.
� АС.
Точка А не лежит в плоскости �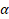 �. Из точки А проведены перпендикуляр АН и наклонная АВ. Найдите длину проекции наклонной на плоскость �
�. Из точки А проведены перпендикуляр АН и наклонная АВ. Найдите длину проекции наклонной на плоскость �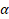 �, если АН =5, АВ = 13.
�, если АН =5, АВ = 13.
| А) �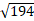 �; �; | Б) 12; | В) 8. |
Точка А не лежит в плоскости �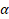 �. Из точки А проведены перпендикуляр АН и наклонная АВ. Найдите длину проекции наклонной на плоскость �
�. Из точки А проведены перпендикуляр АН и наклонная АВ. Найдите длину проекции наклонной на плоскость �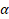 �, если АВ = 8 и угол между перпендикуляром и наклонной равен 600.
�, если АВ = 8 и угол между перпендикуляром и наклонной равен 600.
| А) �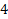 �; �; | Б) 4�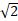 �; �; | В) 4�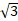 �. �. |
Точка А не лежит в плоскости �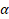 �. Из точки А проведена наклонная АВ под углом 450 к плоскости . Найдите длину перпендикуляра АН, если наклонная АВ = 6.
�. Из точки А проведена наклонная АВ под углом 450 к плоскости . Найдите длину перпендикуляра АН, если наклонная АВ = 6.
| А) �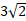 �; �; | Б) 3�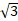 �; �; | В) 6�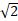 �. �. |
ЧАСТЬ Б
АВСД – квадрат. ВР�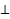 � (АВС). Найдите РД, если ВР = 4 и �
� (АВС). Найдите РД, если ВР = 4 и �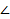 �РСВ = 300
�РСВ = 300






Из точки А к плоскости �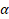 � проведены две наклонные АВ и АС, образующие с плоскостью углы в 300 и 600соответственно. Найдите расстояние между основаниями наклонных, если длина перпендикуляра АН= 9 и проекции этих наклонных взаимно перпендикулярны.
� проведены две наклонные АВ и АС, образующие с плоскостью углы в 300 и 600соответственно. Найдите расстояние между основаниями наклонных, если длина перпендикуляра АН= 9 и проекции этих наклонных взаимно перпендикулярны.
Вариант 2.
ЧАСТЬ А.
Какие из утверждений верны:
А) Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости.
Б) Углом между прямой и плоскостью называется угол между этой прямой и её проекцией на данную плоскость
В) Если к плоскости проведены две наклонные, то они равны.
Г) Если две прямые перпендикулярны плоскости, то они пересекаются.
Справедливы ли утверждения:
А) АВСД- параллелограмм, АК�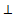 � АВ, значит ВС�
� АВ, значит ВС�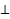 � АК.
� АК.
Б) АВСД –прямоугольник, ВР �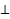 � (АВС), значит треугольник РСД – прямоугольный.
� (АВС), значит треугольник РСД – прямоугольный.
В) АВСД – квадрат, ВД�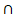 �АС=О, ОЕ�
�АС=О, ОЕ�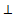 � ВД, значит ОЕ�
� ВД, значит ОЕ� � АС.
� АС.
Точка А не лежит в плоскости �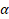 �. Из точки А проведены перпендикуляр АН и наклонная АВ. Найдите длину перпендикуляра АН, если АВ= 10, НВ = 6.
�. Из точки А проведены перпендикуляр АН и наклонная АВ. Найдите длину перпендикуляра АН, если АВ= 10, НВ = 6.
| А) �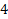 �; �; | Б) 8; | В) 2. |
Точка А не лежит в плоскости �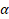 �. Из точки А проведены перпендикуляр АН и наклонная АВ. Найдите длину наклонной АВ , если АН = 4 и угол между перпендикуляром и наклонной равен 450.
�. Из точки А проведены перпендикуляр АН и наклонная АВ. Найдите длину наклонной АВ , если АН = 4 и угол между перпендикуляром и наклонной равен 450.
| А) �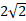 �; �; | Б) 4�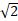 �; �; | В) 2�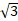 �. �. |
Точка А не лежит в плоскости �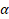 �. Из точки А проведена наклонная АВ под углом 600 к плоскости . Найдите длину проекции наклонной, если наклонная АВ = 12.
�. Из точки А проведена наклонная АВ под углом 600 к плоскости . Найдите длину проекции наклонной, если наклонная АВ = 12.
| А)�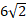 �; �; | Б) 6�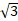 �; �; | В) 6. |
ЧАСТЬ Б
АВСД – прямоугольник. ВР�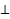 � (АВС). Найдите РД, если АВ= 4, ВС = 6 и �
� (АВС). Найдите РД, если АВ= 4, ВС = 6 и �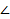 �РСВ = 300
�РСВ = 300






Из точки А к плоскости �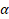 � проведены две наклонные АВ и АС, образующие с плоскостью углы в 300. Найдите расстояние между основаниями наклонных, если длина перпендикуляра АН= 6 и угол между их проекциями 1200
� проведены две наклонные АВ и АС, образующие с плоскостью углы в 300. Найдите расстояние между основаниями наклонных, если длина перпендикуляра АН= 6 и угол между их проекциями 1200
Нормы оценок:
«2» 0-2
«3» 3-4
«4» 5-6
«5» 7-8
ОТВЕТЫ:
|
| Часть А | Часть Б |
|
| 1 | 2 | 3 | 4 | 5 | 1 | 2 |
| А | Б | В |
| Вариант 1 | БГ | да | да | нет | Б | В | А | 2�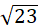 � � | 18 |
| Вариант 2. | АБ | нет | да | да | Б | А | В | 8 | 6 |
Контрольная работа по теме: «Многогранники»
Вариант 1
1) Основание прямой призмы — прямоугольный треугольник с катетами 6 и 8 см. Найдите площадь боковой поверхности призмы, если ее наибольшая боковая грань — квадрат.
2) Боковое ребро правильной четырехугольной пирамиды равно 4 см и образует с плоскостью основания пирамиды угол 45°.
а) Найдите высоту пирамиды.
б) Найдите площадь боковой поверхности пирамиды.
3) Ребро правильного тетраэдра DABC равно а. Постройте сечение тетраэдра, проходящее через середину ребра DA параллельно плоскости DBC, и найдите площадь этого сечения.
Вариант 2
1) Основание прямой призмы — прямоугольный треугольник с гипотенузой 13 см и катетом 12 см. Найдите площадь боковой поверхности призмы, если ее наименьшая боковая грань — квадрат.
2) Высота правильной четырехугольной пирамиды равна √6 см, а боковое ребро наклонено к плоскости основания под углом 60°.
а) Найдите боковое ребро пирамиды.
б) Найдите площадь боковой поверхности пирамиды.
3) Ребро правильного тетраэдра DABC равно а. Постройте сечение тетраэдра, проходящее через середины ребер DA и АВ параллельно ребру ВС, и найдите площадь этого сечения.
Нормы оценок:
«2» 0
«3» 1
«4» 2
«5» 3
Зачетное занятие.
Вариант 1
1.Тело, поверхность которого состоит из конечного числа плоских многоугольников, называется:
а)четырехугольник
б)многоугольник
в)многогранник
г)шестиугольник
2. К многогранникам относятся:
а)параллелепипед
б)призма
с)пирамида
все ответы верны
3. Отрезок, соединяющий две вершины призмы, не принадлежащие одной грани называется:
а)диагональю
б)ребром
в)гранью
г)осью
4. У призмы боковые ребра:
а)равны
б)симметричны
в)параллельны и равны
г)параллельны
5. Грани параллелепипеда не имеющие общих вершин, называются:
а)противолежащими
б)противоположными
в)симметричными
г)равными
6. Перпендикуляр, опущенный из вершины пирамиды на плоскость основания, называется:
а)медианой
б)осью
в)диагональю
г)высотой
7. Точки не лежащие в плоскости основания пирамиды, называются:
а)вершинами пирамиды
б)боковыми ребрами
в)линейным размером
г)вершинами грани
8. Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется:
а)медианой
б)апофемой
в)перпендикуляром
г)биссектрисой
9. У куба все грани:
а)прямоугольники
б)квадраты
в)трапеции
г)ромбы
10. Тело, состоящее из двух кругов и всех отрезков, соединяющих точки кругов называется:
а)конусом
б)шаром
в)цилиндром
г)сферой
11. У цилиндра образующие:
а)равны
б)параллельны
в)симметричны
г)параллельны и равны
12. Основания цилиндра лежат в:
а)одной плоскости
б)равных плоскостях
в)параллельных плоскостях
г)разных плоскостях
13. Поверхность конуса состоит из:
а)образующих
б)граней и ребер
в)основания и ребра
г)основания и боковой поверхности
14. Отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара, называется:
а)радиусом
б)центром
в)осью
г)диаметром
15. Всякое сечение шара плоскостью есть:
а)окружность
б)круг
в)сфера
г)полукруг
16. Сечение шара диаметральной плоскостью называется:
а)большим кругом
б)большой окружностью
в)малым кругом
г)окружностью
17. Круг конуса называется:
а)вершиной
б)плоскостью
в)гранью
г)основанием
18. Основания призмы:
а)параллельны
б)равны
в)перпендикулярны
г)не равны
19. Площадью боковой поверхности призмы называется:
а)сумма площадей боковых многоугольников
б)сумма площадей боковых ребер
в)сумма площадей боковых граней
г)сумма площадей оснований
20. Пересечения диагоналей параллелепипеда является его:
а)центром
б)центром симметрии
в)линейным размером
г)точкой сечения
Вариант 2
1. Вершины многогранника обозначаются:
а)а, в, с, д ...
б)А, В, С, Д ...
в)ав, сд, ас, ад ...
г)АВ, СВ, АД, СД ...
2. Многогранник, который состоит из двух плоских многоугольников, совмещенных параллельным переносом, называется:
а)пирамидой
б)призмой
в)цилиндром
г)параллелепипедом
3. Если боковые ребра призмы перпендикулярны основанию, то призма является:
а)наклонной
б)правильной
в)прямой
г) выпуклой
4. Если в основании призмы лежит параллелограмм, то она является:
а)правильной призмой
б)параллелепипедом
в)правильным многоугольником
г)пирамидой
5. Многогранник, который состоит из плоского многоугольника, точки и отрезков соединяющих их, называется:
а)конусом
б)пирамидой
в)призмой
г)шаром
6. Отрезки, соединяющие вершину пирамиды с вершинами основания, называются:
а)гранями
б)сторонами
в)боковыми ребрами
г)диагоналями
7. Треугольная пирамида называется:
а)правильной пирамидой
б)тетраэдром
в)треугольной пирамидой
г)наклонной пирамидой
8. К правильным многогранникам не относится:
а)куб
б)тетраэдр
в)икосаэдр
г)пирамида
9. Высота пирамиды является:
а)осью
б)медианой
в)перпендикуляром
г)апофемой
10. Отрезки, соединяющие точки окружностей кругов, называются:
а)гранями цилиндра
б)образующими цилиндра
в)высотами цилиндра
г)перпендикулярами цилиндра
11. Прямая, проходящая через центры оснований называется:
а)осью цилиндра
б)высотой цилиндра
в)радиусом цилиндра
г)ребром цилиндра
12. Тело, которое состоит из точки, круга и отрезков соединяющих их, называется:
а)пирамидой
б)конусом
в)шаром
г)цилиндром
13. Тело, которое состоит из всех точек пространства, называется:
а)сферой
б)шаром
в)цилиндром
г) полусферой
14. Граница шара называется:
а)сферой
б)шаром
в)сечением
г)окружностью
15. Линия пересечения двух сфер есть:
а)круг
б)полукруг
в)окружность
г)сечение
16. Сечение сферы называется:
а)кругом
б)большой окружностью
в)малым кругом
г) малой окружностью
17. Грани выпуклого многогранника являются выпуклыми:
а)треугольниками
б)углами
в)многоугольниками
г)шестиугольниками
18. Боковая поверхность призмы состоит из:
а)параллелограммов
б)квадратов
в)ромбов
г)треугольников
19. Боковая поверхность прямой призмы равна:
а)произведению периметра на длину грани призмы
б)произведению длины грани призмы на основание
в)произведению длины грани призмы на высоту
г)произведению периметра основания на высоту призмы
20. К правильным многогранникам относятся:
а)тетраэдр
б)куб и додекаэдр
в)октаэдр и икосаэдр
г)все ответы верны
Нормы оценок:
«2» 0-5
«3» 6-10
«4» 11-15
«5» 16-20
Ответы на банк тестовых заданий по теме «Многогранники»
Вариант 1
| № вопроса | Правильный ответ |
| в |
| г |
| 3. | а |
| 4. | в |
| 5. | а |
| 6. | г |
| 7. | а |
| 8. | б |
| 9. | б |
| 10. | в |
| 11. | г |
| 12. | в |
| 13. | г |
| 14. | г |
| 15. | б |
| 16. | а |
| 17. | г |
| 18. | б |
| 19. | в |
| 20 | б |
Вариант 2
| № вопроса | Правильный ответ |
| 1. | б |
| 2. | б |
| 3. | в |
| 4. | б |
| 5. | б |
| 6. | в |
| 7. | б |
| 8. | г |
| 9. | в |
| 10. | б |
| 11. | а |
| 12. | б |
| 13. | б |
| 14. | а |
| 15. | в |
| 16. | б |
| 17. | в |
| 18. | а |
| 19. | г |
| 20. | г |
Итоговая контрольная работа.
Вариант 1.
1. Сторона основания правильной треугольной призмы равна 6см, а диагональ боковой грани равна 10 см. Найдите высоту призмы, площадь боковой и полной поверхностей призмы, объем.
2. Основание пирамиды – прямоугольник состоронами 6см и 8см. Высота пирамиды равна 12 см и проходит через точку пересечения диагоналей основания. Найдите боковые ребра пирамиды и объем.
3. Диагональ прямоугольного параллелепипеда
равна 25 см, а диагональ одной из его граней 24 см. Найдите длину ребра, перпендикулярного к данной грани.
4. Высота правильной треугольной пирамиды равна 8 см, а боковое ребро 10 см. Найдите площадь боковой поверхности пирамиды.
5. В правильной четырехугольной призме проведено сечение через диагональ нижнего основания и конец непараллельной ей диагонали верхнего основания. Площадь основания и площадь сечения равны 20 см2. Найдите объем призмы.
6. Прямоугольник со сторонами 12 см и 16 см может быть двумя способами свернут в виде боковой поверхности правильной четырехугольной призмы. Сравните объемы этих призм.
Вариант 2.
1. Боковое ребро правильной треугольной призмы равно 9см., а диагональ боковой грани равна 15см. Найдите сторону основания, площадь боковой и полной поверхностей призмы, объем.
2. Основание пирамиды – ромб с диагоналями 10 и 18см. Высота пирамиды проходит через точку пересечения диагоналей ромба. Меньшее боковое ребро пирамиды равно 13см. Найдите высоту пирамиды, большее боковое ребро и объем.
3. Диагональ одной из граней прямоугольного параллелепипеда равна 15см., а ребро, перпендикулярное к этой грани, имеет длину 8см. Найдите диагональ параллелепипеда.
4. Высота правильной четырехугольной пирамиды равна 16см., а боковое ребро 20см. Найдите площадь боковой поверхности пирамиды.
5. В правильной прямоугольной призме проведено сечение через сторону нижнего основания и середину противолежащего бокового ребра. Плоскость сечения наклонена к плоскости основания под углом 45º; площадь сечения равна 4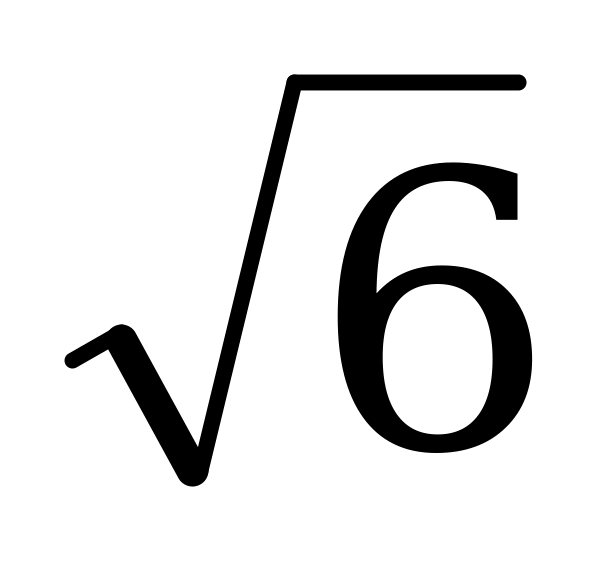 см2. Найдите объем призмы.
см2. Найдите объем призмы.
6. Прямоугольник со сторонами 24 см. и 10 см. может быть двумя способами свернут в виде боковой поверхности правильной четырехугольной призмы. Сравните площади полных поверхностей этих призм.
Нормы оценок:
«2» 0-1
«3» 2-3
«4» 4-5
«5» 5-6
Зачетное занятие.
1 вариант
1. Радиус основания цилиндра 1,5 см, высота 4см. Найти диагональ осевого сечения.
А) 4,2 см; Б) 10 см; В) 5 см.
2. Осевое сечение цилиндра – квадрат площадью 36 дм2. Найти площадь основания цилиндра.
А) 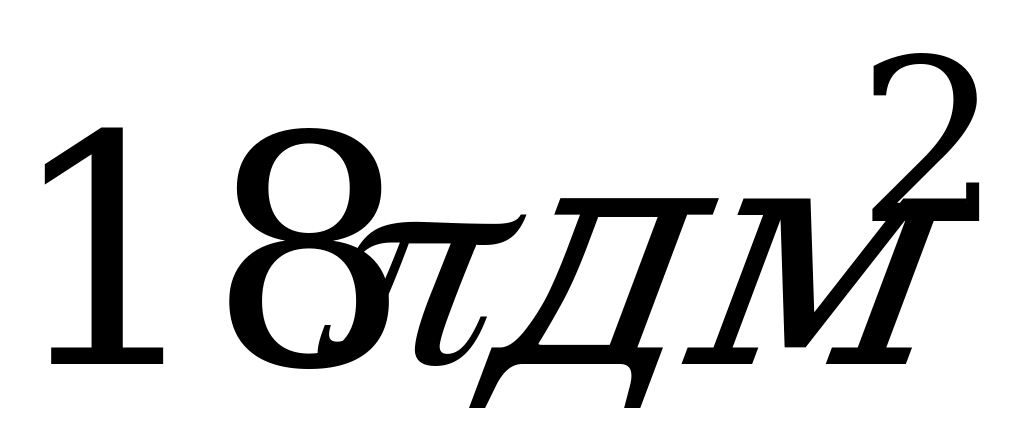 ; Б)
; Б) 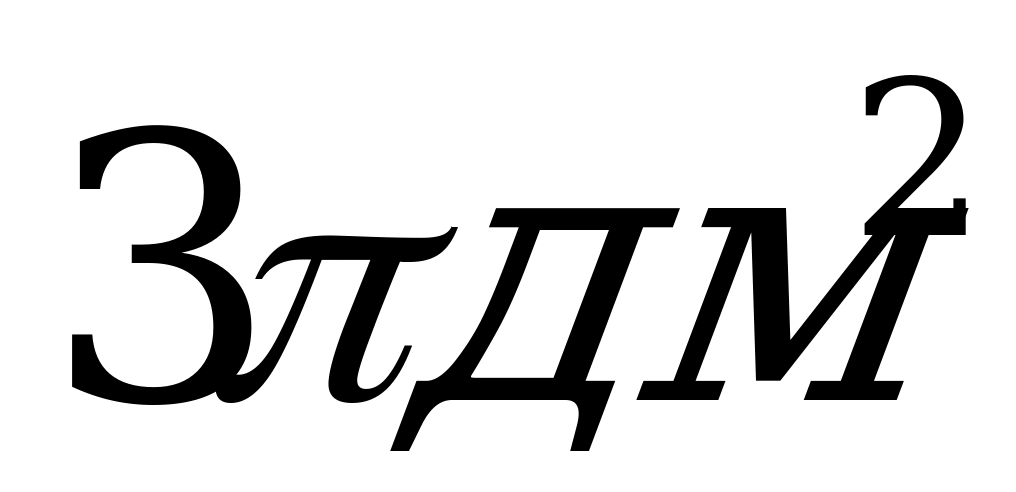 ; В)
; В) 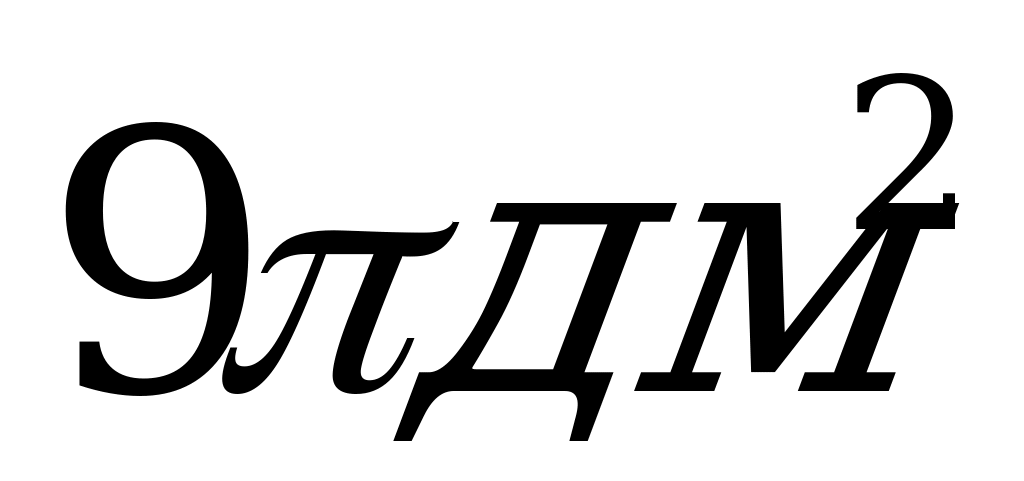 .
.
3. Площадь осевого сечения конуса равна 48 см2, высота 12. Найдите R.
А) 4 см; Б) 2 см; В) 8 см.
4. Квадрат со стороной 4 см вращается вокруг своей стороны. Чему равна площадь основания полученного тела?
А)  ; Б)
; Б)  ; В)
; В) 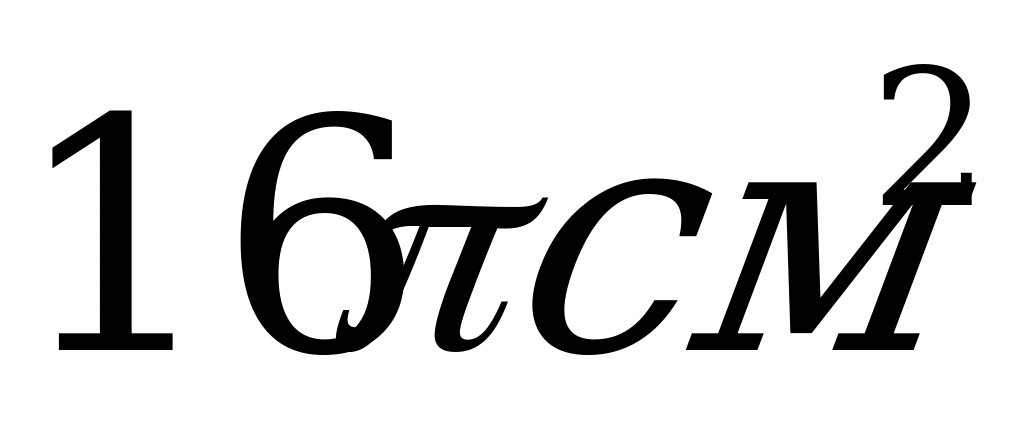 .
.
5. Наибольший угол между образующими конуса 600 . Чему равен диаметр основания, если образующая равна 5 см?
А) 5 см; Б) 10 см; В) 2,5 см.
6. Высота цилиндра равна 4 см, радиус 1 см. Найти площадь осевого сечения.
А) 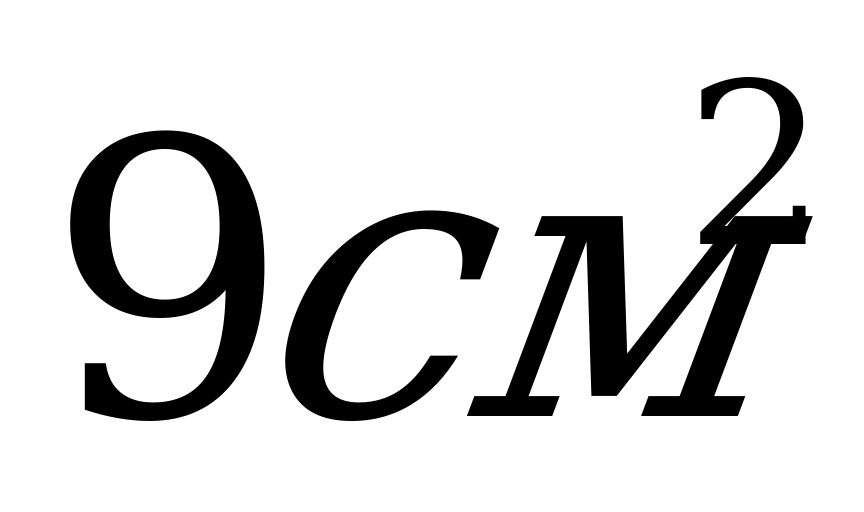 ; Б)
; Б) 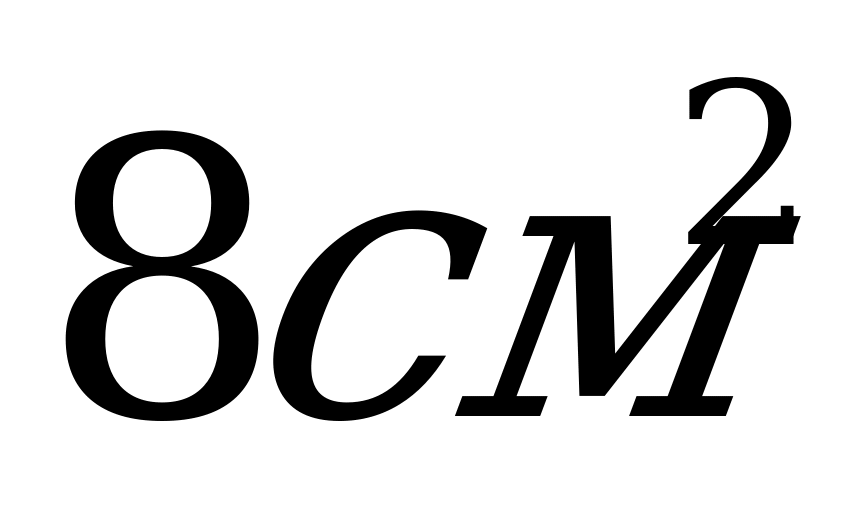 ; В)
; В) 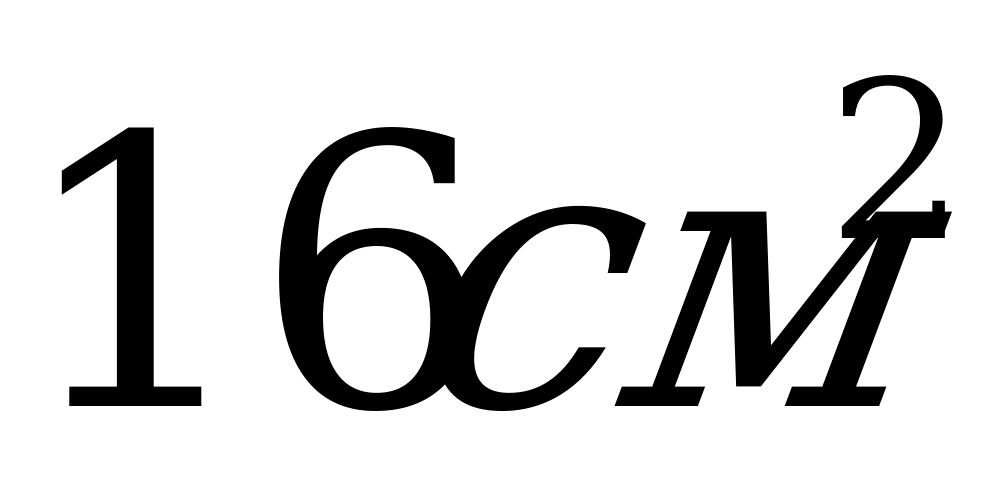 .
.
7. Радиусы оснований усеченного конуса равны 15 см и 12 см, высота 4 см. Чему равна образующая конуса?
А) 5 см; Б) 4 см; В) 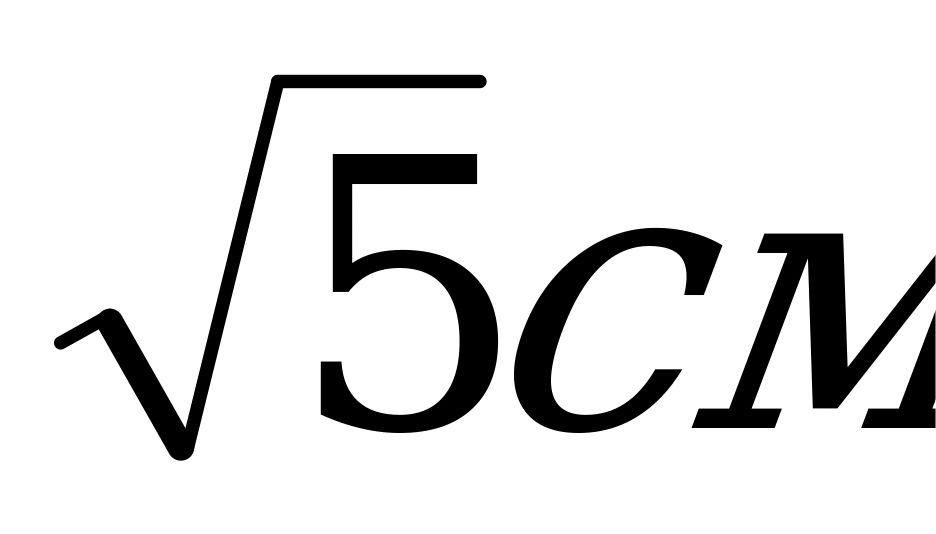 .
.
8. В равностороннем цилиндре радиус основания равен 3,5 см. Чему равна площадь осевого сечения?
А) 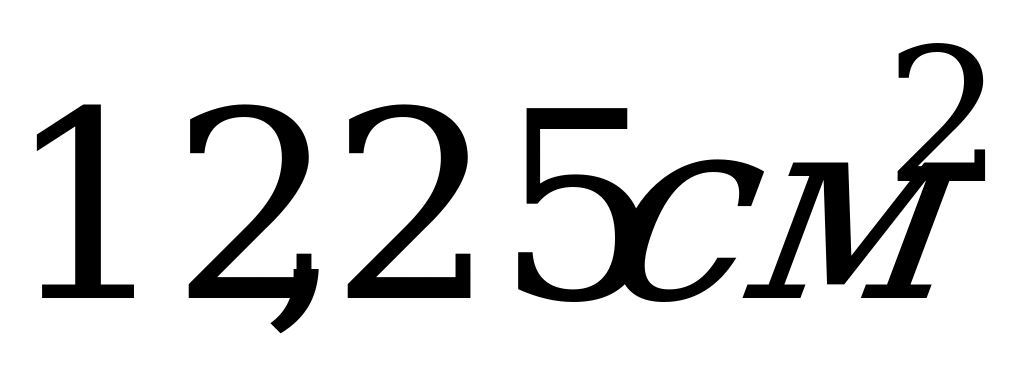 ; Б)
; Б) 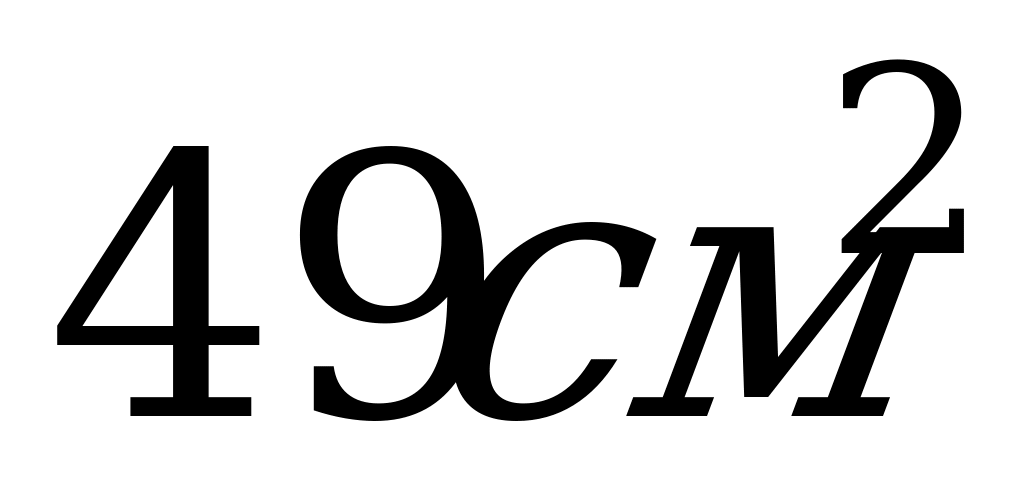 ; В)
; В) 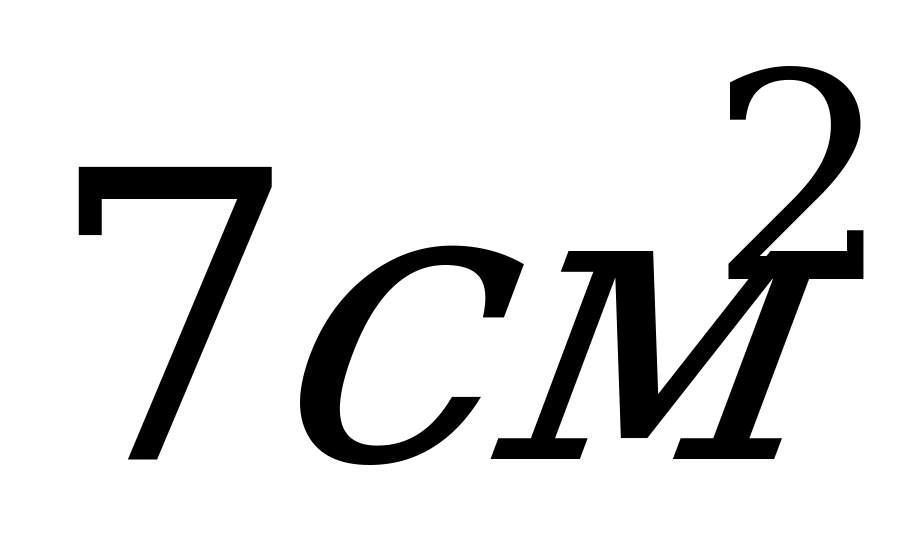 .
.
9. В равностороннем конусе образующая равна 8 см. Чему равна длина окружности основания?
А) 8π см; Б) 4 π см; В) 16 π см.
А) 1; Б) бесконечно много; В) 2.
10. В равностороннем конусе образующая равна 8 см. Чему равна площадь осевого сечения?
А) 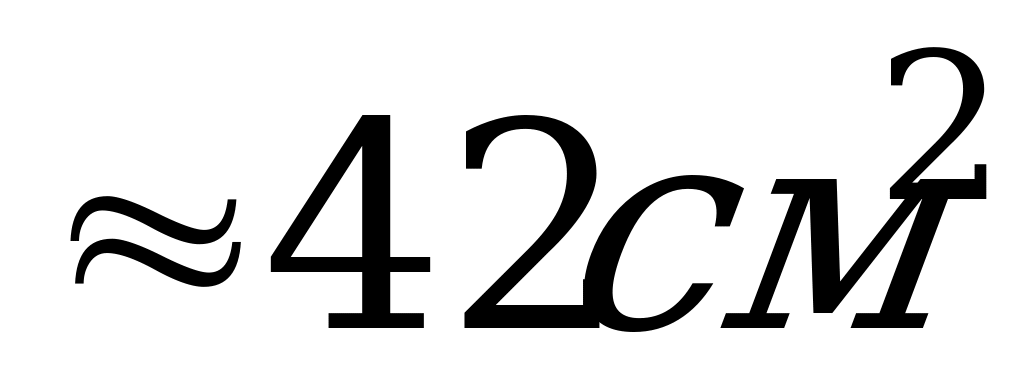 ; Б)
; Б) 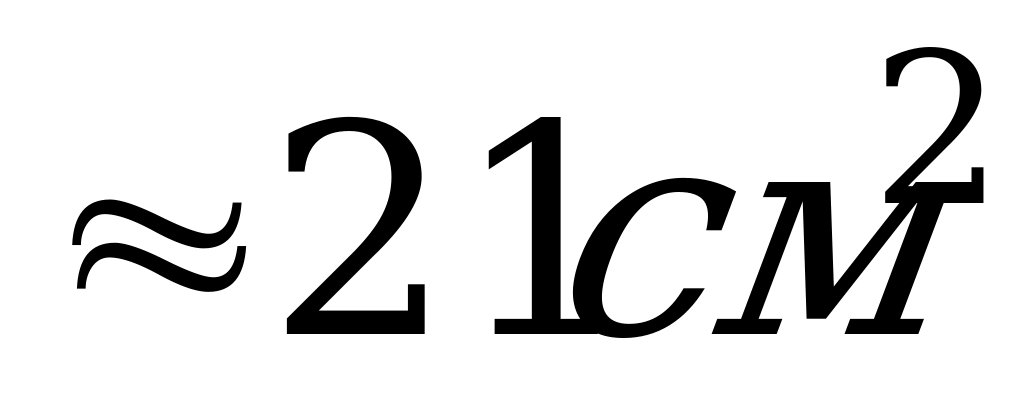 ; В)
; В) 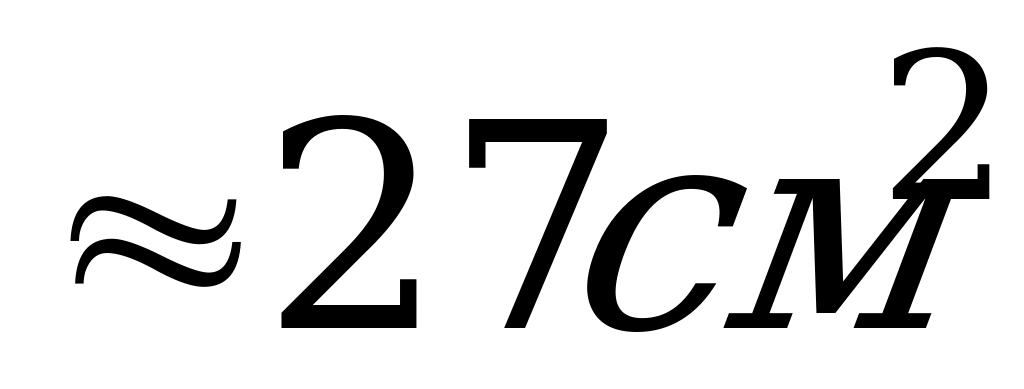 .
.
2 вариант
1. Радиус основания цилиндра 2,5 см, высота 12см. Найти диагональ осевого сечения.
А) 15 см; Б) 14 см; В) 13 см.
2. Осевое сечение цилиндра – квадрат, площадью 16 дм2 . Найти площадь основания цилиндра.
А)  ; Б)
; Б) 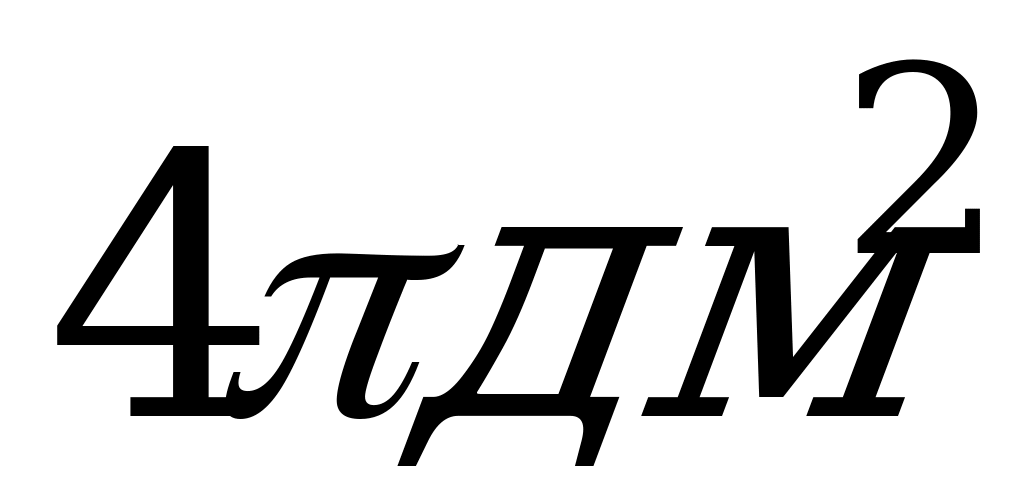 ; В)
; В) 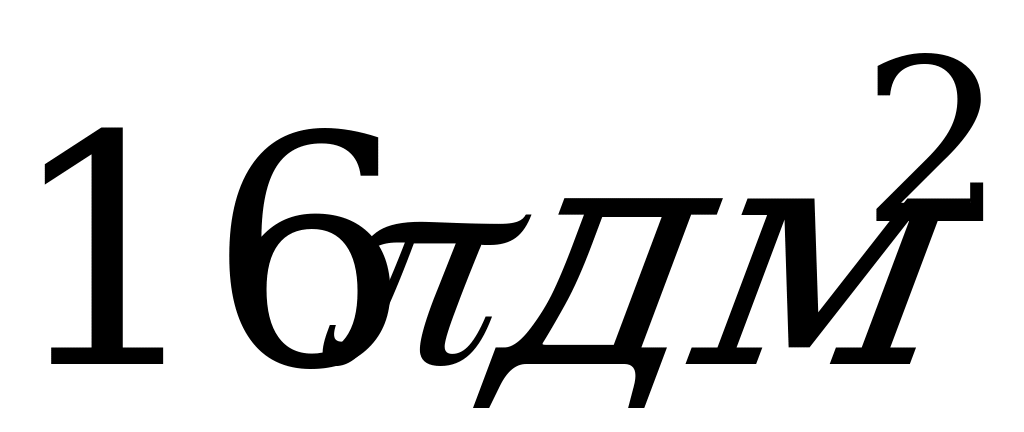 .
.
3. Площадь осевого сечения конуса равна 36 см2, высота 12. Найдите R.
А) 3 см; Б) 1,5 см; В) 6 см.
4. Квадрат со стороной 3 см вращается вокруг своей стороны. Чему равна площадь основания полученного тела?
А)  ; Б)
; Б)  ; В)
; В) 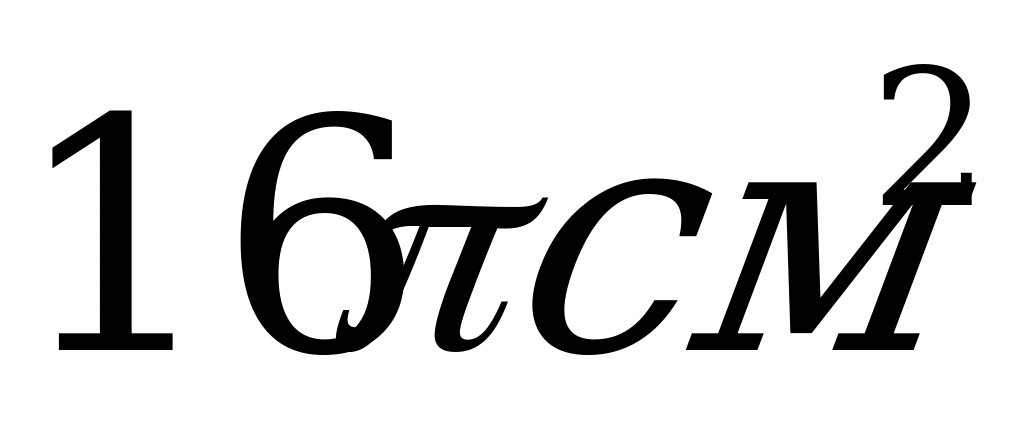 .
.
5. Наибольший угол между образующими конуса 600 . Чему равен диаметр основания, если образующая равна 7 см?
А) 7 см; Б) 14 см; В) 3,5 см.
6. Высота цилиндра равна 8 см, радиус 1 см. Найти площадь осевого сечения.
А) 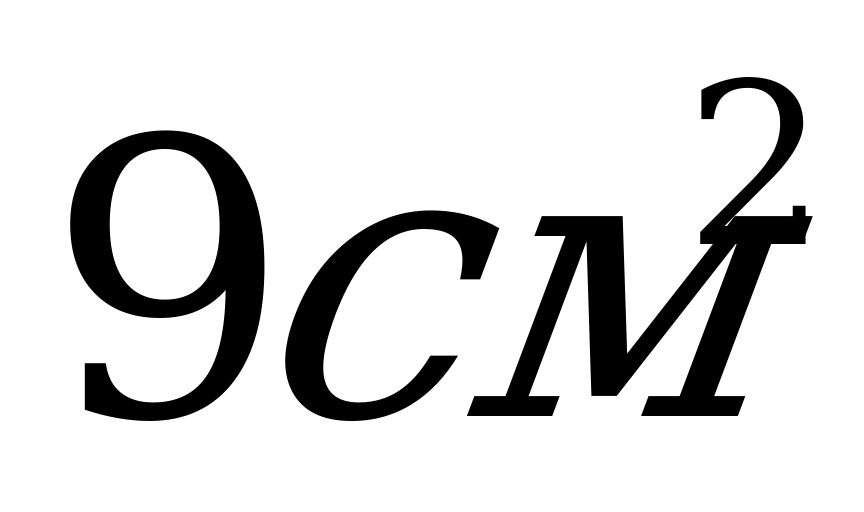 ; Б)
; Б) 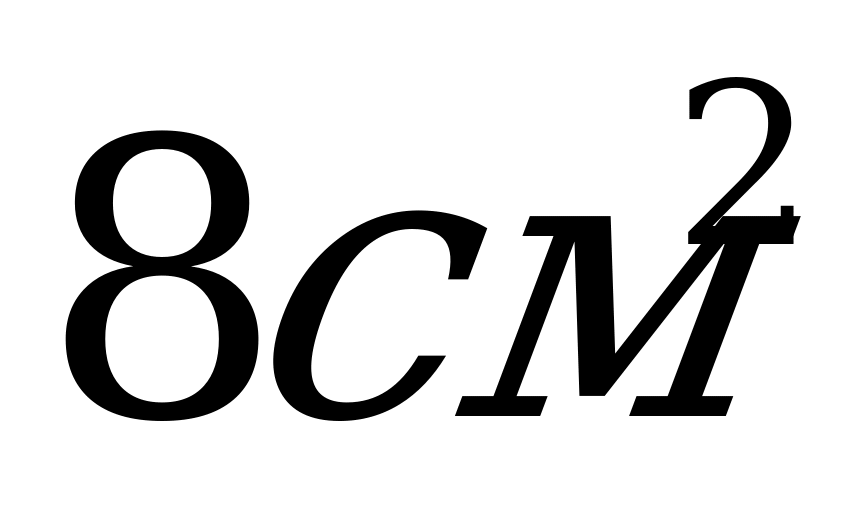 ; В)
; В) 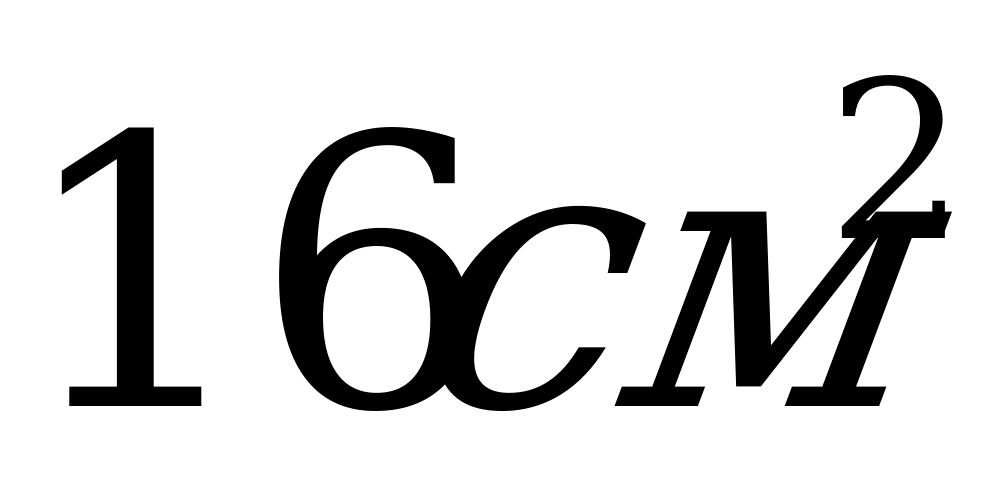 .
.
7. Радиусы оснований усеченного конуса равны 6 см и 12 см, высота 8 см. Чему равна образующая конуса?
А) 10 см; Б) 4 см; В) 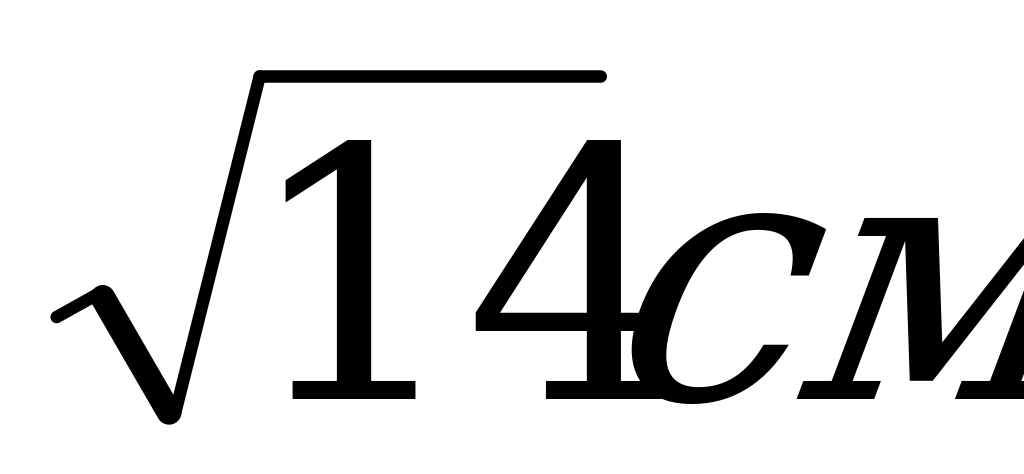 .
.
8. В равностороннем цилиндре радиус основания равен 7,5 см. Чему равна площадь осевого сечения?
А) 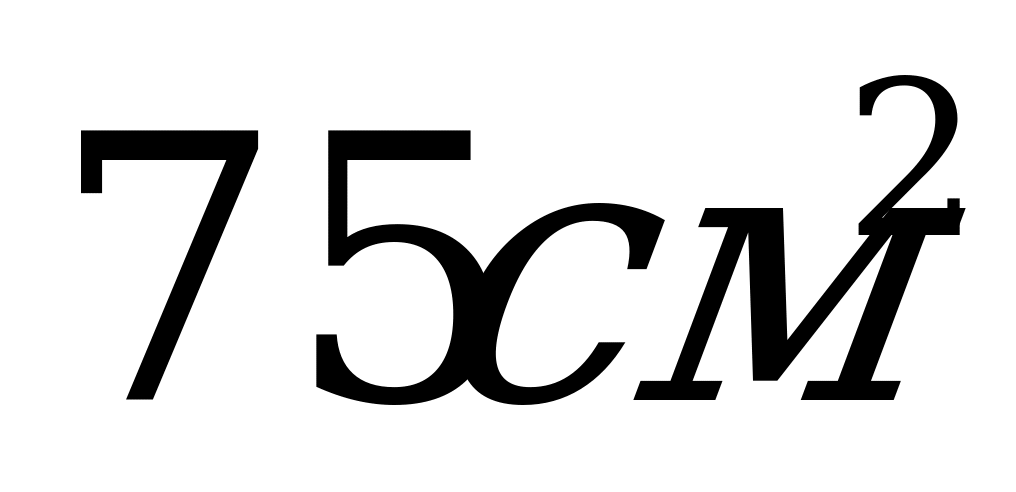 ; Б)
; Б) 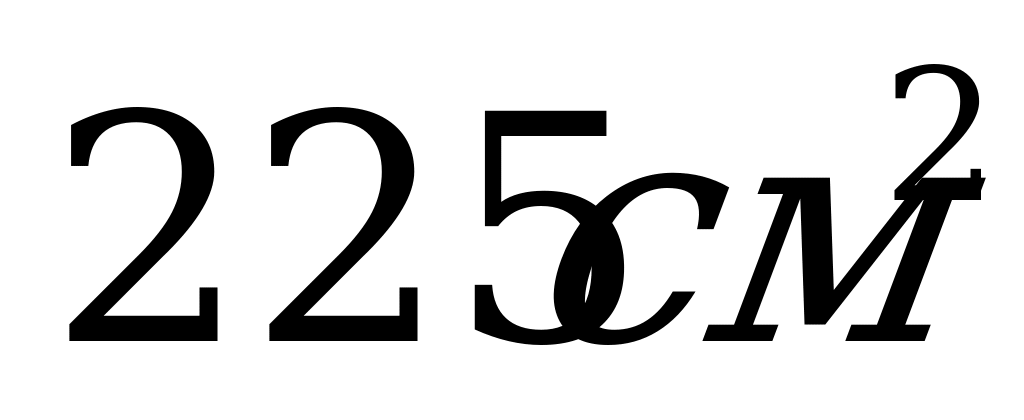 ; В)
; В) 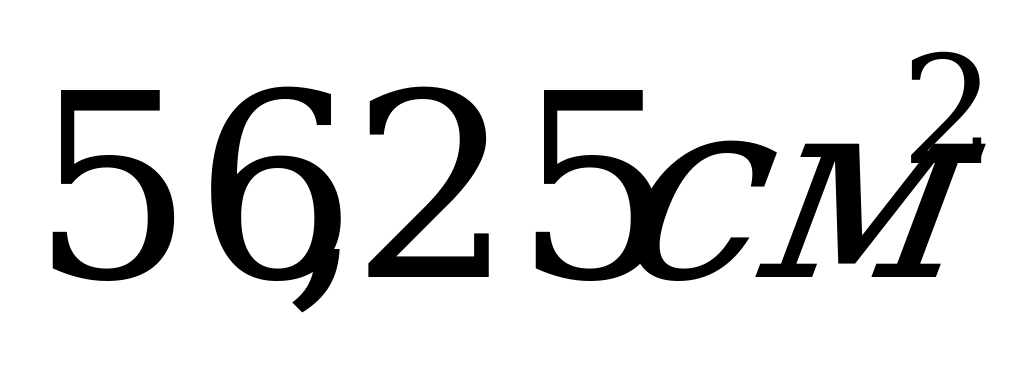 .
.
9. В равностороннем конусе образующая равна 6 см. Чему равна длина окружности основания?
А) 12 π см; Б) 6 π см; В) 9 π см.
10. В равностороннем конусе образующая равна 8 см. Чему равна площадь осевого сечения?
А) 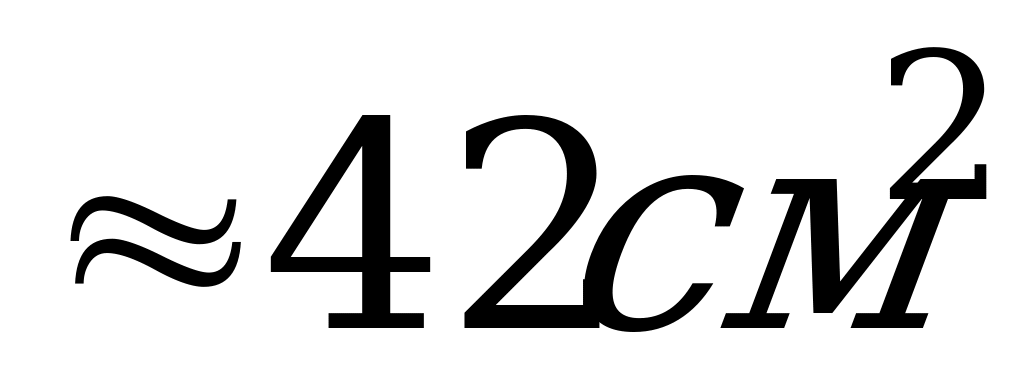 ; Б)
; Б) 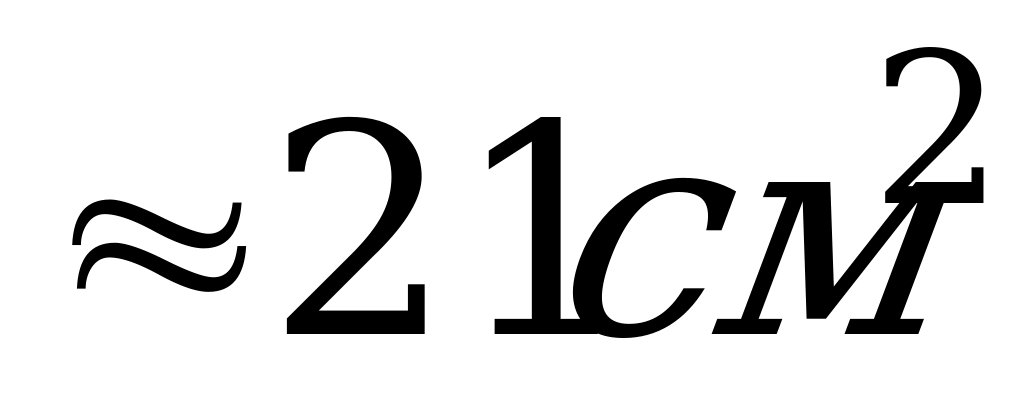 ; В)
; В) 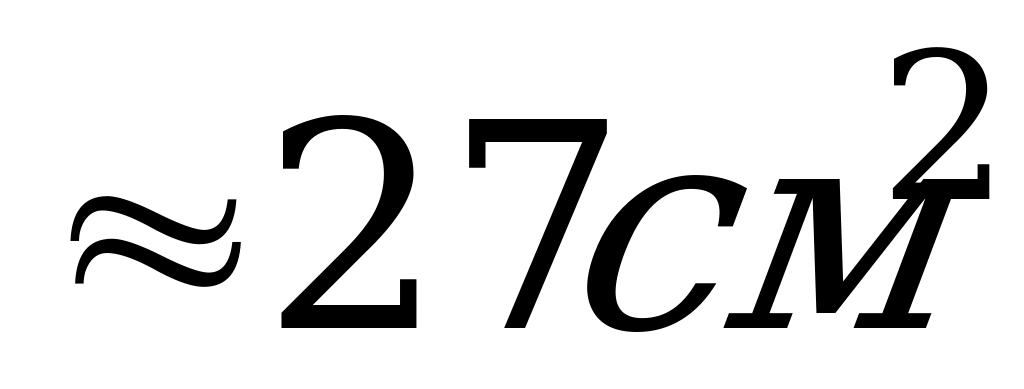 .
.
Нормы оценок:
«2» 0-2
«3» 3-5
«4» 6-8
«5» 9-10
Контрольная работа по теме: «Тела вращения. Объемы тел»
|
| ВАРИАНТ I | ОТВЕТЫ |
| № | Задание | а | б | в |
| 1 | Формула площади круга | 2πR | πR2 | 2πR2 |
| 2 | При вращении прямоугольника вокруг стороны получится | шар | конус | цилиндр |
| 3 | В основании цилиндра лежит | круг | полукруг | квадрат |
| 4 | Отрезки, соединяющие соответствующие точки окружностей в цилиндре называются | высотой | осью | образующими |
| 5 | Сечение цилиндра плоскостью, параллельной его оси есть | прямоугольник | круг | трапеция |
| 6 | Радиус основания цилиндра равна 8 см, высота цилиндраравна 5 см. Найдите площадь осевого сечения цилиндра | 40 см2 | 80 см2 | 20 см2 |
| 7 | Конус получается при вращении вокруг катета | Произвольного треугольника | Равностороннего треугольника | Прямоугольного треугольника |
| 8 | Осевое сечение конуса - это | треугольник | круг | прямоугольник |
| 9 | Формула площади боковой поверхности конуса | Sбок = πRl | Sбок = πR2l | Sбок =2 πRl |
| 10 | Формула площади боковой поверхности цилиндра | Sбок = 2πRh | Sбок= πR2h | Sбок= πRh |
| 11 | Сечение конуса плоскостью, проходящее перпендикулярно его оси, это | трапеция | треугольник | круг |
| 12 | Радиус основания конуса 3 см, высота 4 см. Найдите образующую | 7 см | 5 см | 1 см |
| 13 | Сфера - это поверхность | шара | цилиндра | конуса |
| 14 | Формула площади сферы | 2πR2 | 4πR2 | πR2 |
| 15 | Площадь сферы равна 36π см2. Чему равен радиус шара | 3 см | 9 см | 6 см |
| 16 | Любое сечение шара плоскостью – это | квадрат | круг | прямоугольник |
| 17 | Осевым сечением усеченного конуса является | прямоугольник | треугольник | трапеция |
| 18 | Что представляет из себя геометрическое место точек, удаленных от данной точки на расстояние, меньшее или равное 10 см. | шар радиуса 5 см | шар радиуса 20 см | шар радиуса 10 см |
| 19 | Формула длины окружности | 2πR | πR2 | 2πR2 |
| 20 | Пересечение двух сфер - это | круг | окружность | шар |
|
| ВАРИАНТ II | ОТВЕТЫ |
| № | Задание | а | б | в |
| 1 | Формула длины окружности | πR2 | 2πR | 2πR2 |
| 2 | Сечение цилиндра плоскостью, проходящее перпендикулярно его оси | прямоугольник | треугольник | круг |
| 3 | Формула площади боковой поверхности цилиндра | Sбок= πRh | Sбок = 2πRh | Sбок= πR2h |
| 4 | Высота конуса 6 см, радиус его основания 8 см. найдите длину образующей конуса. | 10 см | 14 см | 2 см |
| 5 | Боковая поверхность цилиндра состоит из | осей | высот | образующих |
| 6 | Формула площади круга | πR2 | 2πR | 2πR2 |
| 7 | Сечение конуса плоскостью, проходящее через его вершину, это | прямоугольник | трапеция | треугольник |
| 8 | Осевое сечение усеченного конуса это | круг | трапеция | треугольник |
| 9 | Геометрическое место точек, удаленных от данной точкина расстояние меньшее или равное 5 см это | Шар радиуса 5 см | Шар радиуса 10 см | Шар радиуса 2,5 см |
| 10 | Сечение шара плоскостью – это | овал | окружность | круг |
| 11 | Площадь сферы равна 100 π см2. Чему равен радиус соответствующего шара | 10 см | 5 см | 25 см |
| 12 | При вращении прямоугольника вокруг его стороны получается | цилиндр | шар | конус |
| 13 | Площадь боковой поверхности конуса | Sбок =2 πRl | Sбок = πRl | Sбок = πR2l |
| 14 | При вращении прямоугольного треугольника вокруг катетаполучится | цилиндр | шар | конус |
| 15 | Сечение конуса плоскость, прохо-дящее перпендикулярно оси есть | прямоугольник | круг | трапеция |
| 16 | Радиус основания цилиндра – 3 см, высота – 7 см. найдите площадь осевого сечения цилиндра | 42 см2 | 21 см2 | 10 см2 |
| 17 | Отрезок, соединяющий вершину конуса с точками окружности основания, называется | осью | образующей | высотой |
| 18 | Сечение цилиндра плоскостью, параллельно его оси это | прямоугольник | круг | треугольник |
| 19 | Сфера это поверхность | цилиндра | конуса | шара |
| 20 | Формула площади сферы | πR2 | 2πR2 | 4πR2 |
Ответы
| 1 вариант |
| | | | | | | | | | | | | | | | | | | |
| б | в | а | в | а | б | в | а | а | а | в | б | а | б | а | б | в | в | а | б |
| 2 вариант |
| | | | | | | | | | | | | | | | | | | |
| а | в | б | а | в | а | в | б | а | в | б | а | б | в | б | а | б | а | в | в |
Нормы оценок:
«2» 0-5
«3» 6-10
«4» 11-15
«5» 16-20
Итоговая контрольная работа.
Вариант 1.
1. Какое из следующих утверждений неверно?
а) длиной ненулевого вектора АВ называется длина отрезка АВ;
б) нулевой вектор считается сонаправленным любому вектору;
в) разностью векторов а и b называется такой вектор. сумма которого с вектором b равна вектору а;
г) векторы называются равными, если равны их длины.
2. Упростите выражение:СС1+СВ+СД+А1В1, если ABCDA₁B₁C₁D₁ - параллелепипед.
а) AC ; б) 0 ; в) СВ1; г) DC ; д) BA .
3. Какие из следующих утверждений верны?
а) противоположные векторы равны;
б) Векторы, лежащие на двух прямых, перпендикулярных к одной плоскости, коллинеарны
в) произведение вектора на число является число;
г) Для сложения двух векторов на плоскости используют правило параллелограмма.
4. Дан куб ABCDA₁B₁C₁D₁ . Найдите угол между DC1 и СВ.
а) 45о; б) 30о; в) 135о ; г) 90о ; д) 60о .
5. Какие из следующих утверждений неверны?
а) векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости;
б) если вектор с можно разложить по векторам а и b, т.е. представить в виде с=ха+yb, где х, y- некоторые числа, то векторы а, b, c компланарны;
в) для сложения трёх некомпланарных векторов используют правило параллелепипеда;
г) любые два вектора компланарны;
6. Диагонали куба АВСД А1В1С1Д1 пересекаются в точке О . Найдите число µ из равенства ДВ1= µОВ1.
7.Известно, что 2 AC = AB + AD , тогда векторы AB, AD являются:
а) некомпланарными; б) сонаправленными; в) коллинеарными;
г) нулевыми; д) компланарными.
8. Даны параллелограммы ABCD и AB₁C₁D₁. Тогда векторы BB1, CC1, DD1:
а) нулевые; б) равные; в) противоположные; г) компланарные;
д) некомпланарные.
9. Найдите соответствие , если А(х,у, z), а В(х1;у1, z1)
| 1.координаты вектора ВА | А) �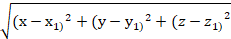 � � |
Скалярное произведение векторов | Б) (αх; αу; αz) |
| 3. абсолютная величина вектора ВА | В) (х-х1; у-у1; z-z1) |
| 4. умножение вектора А на число | Г) хх1+уу1+zz1 |
10. Составить уравнение плоскости, проходящей через точку А и перпендикулярной прямой АВ, если А(-1,2,1), В(-3,1,-2).
11. Площадь треугольника равна 8. Угол между плоскостью треугольника и его ортогональной проекцией равен 45о. Найдите площадь ортогональной проекции треугольника.
Критерии отметки: за каждый правильный ответ даётся по 1 баллу; максимальное количество баллов 11.
11 баллов – «5»;
9-10 баллов – «4»;
6-8 баллов – «3»;
менее 6 баллов – «2».
Вариант 2.
1. Какое из следующих утверждений неверно?
а) длиной нулевого вектора АВ называется длина отрезка АВ ;
б) любая точка пространства рассматривается как нулевой вектор;
г) для любых векторов а и b выполняется равенство а+(- b)= а-b;
д) векторы называются равными, если они сонаправлены и равны их длины.
2. Упростите выражение:В1В+В1С1+В1А1+ДС, если ABCDA₁B₁C₁D₁ - параллелепипед.
а) B1A1; б) 0 ; в) CC1; г) CA; д) B1C .
3. Какие из следующих утверждений верны?
а) любые два вектора компланарны.
б) если векторы a и b коллинеарны и а≠0, то существует такое число k, что b=ka;
в) векторы называются равными, если они сонаправлены;
г) два вектора, коллинеарные ненулевому вектору, сонаправлены;
4. Дан куб ABCДA₁B₁C₁Д1 . Найдите угол между СВ1 и ВА1
|а) 45о ; б) 30о ; в) 100о ; г) 90о ; д) 60о .
5. Какие из следующих утверждений неверны?
а) три вектора будут компланарными, если один из них нулевой;
б) если векторы a, b и с компланарны, то вектор d можно разложить по векторам а, b и с
т.е. представить в виде d=ха+yb+zc, где х, y, z- некоторые числа;
в) для сложения трёх компланарных векторов используют правило параллелограмма;
г) любые два вектора коллинеарны.
6. Диагонали куба АВСД А1В1С1Д1 пересекаются в точке О . Найдите число µ из равенства
С1О= µАС1.
7. Известно, что 2 AC = – AB - AD , тогда векторы AB, AD являются:
а) компланарными; б) некомпланарны; в) коллинеарными; г) сонаправлены; д)
нулевые.
8. Даны параллелограммы ABCD и AB₁C₁D₁. Тогда векторы B1B , C1C , D1D :
а) нулевые; б) равные; в) компланарные; г) некомпланарные;
д) противоположные.
9. Найдите соответствие, если если А(х,у, z), а В(х1;у1, z1)
| 1.площадь ортогональной проекции многоугольника | А) �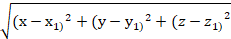 � � |
| 2.координаты середины отрезка | Б)( �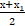 �; � �; �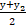 �; � �; �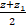 �) �) |
| 3. Скалярное произведение векторов | В) Sф·�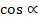 � � |
| 4. . абсолютная величина вектора ВА | Г) хх1+уу1+zz1 |
10. Составить уравнение плоскости, проходящей через точку В и перпендикулярной прямой ВС, если В(-1,-2,2), С(7,0,-9).
11. Площадь ортогональной проекции параллелограмма равна 7. Найдите площадь самого параллелограмма, если угол между плоскостями данных многоугольников равен 60о.
Критерии отметки: за каждый правильный ответ даётся по 1 баллу; максимальное количество баллов 11.
11 баллов – «5»;
9-10 баллов – «4»;
6-8 баллов – «3»;
менее 6 баллов – «2».
Ответы
| № | 1 вариант | 2 вариант |
| 1 | Г | А |
| 2 | В | Д |
| 3 | Б Г | А Б |
| 4 | Г | Д |
| 5 | А Б | Г В |
| 6 | 2 | -1/2 |
| 7 | В | В |
| 8 | Б | Б |
| 9 | 1-в, 2-г, 3-а, 4-б | 1-в, 2-б, 3-г, 4-а |
| 10 | -2х-у-3z+3=0 | 8х+2у-11z+34=0 |
| 11 | 4�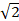 � � | 14 |
Зачетное занятие.
Какой симметрии не существует:
а) тройственной
б) зеркальной
в) осевой
Секущая плоскость α пересекает все образующие неограниченного конуса, кроме одной (которой α параллельна). В сечении получается:
а) дуга окружности
б) парабола
в) окружность
Симметрия относительно плоскости в пространстве называется:
а) центральной
б) осевой
в) зеркальной
Фигура вращения получается в результате вращения плоской фигуры вокруг оси, лежащей в той же плоскости, так ли это:
а) да
б) нет
в) зависит от задачи
Симметрия относительно точки называется:
а) центральной
б) осевой
в) зеркальной
Шар получается вращением полукруга вокруг ограничивающего его диаметра, сфера — вращением полуокружности, так ли это:
а) да
б) нет
в) зависит от задачи
Симметрия относительно прямой называется:
а) центральной
б) осевой
в) зеркальной
Все высоты усеченного конуса:
а) равны
б) перпендикулярны друг другу
в) параллельны основанию
Зная координаты точек A(-12, 7, -3) и B(-10, -2, -2) найдите значение вектора AB:
а) {-2;9;1}
б) {-22;5;-5}
в) {2;-9;1}
Отрезок, соединяющий центры оснований усеченного конуса вращения, является его:
а) диагональю
б) высотой
в) биссектрисой
При каком значении n векторы a(4;2n;-1), b(-1;1;n) перпендикулярны:
а) 4
б) 3
в) 2
Оба основания усеченного конуса вращения:
а) равнобедренные треугольники
б) круги
в) прямоугольные треугольники
Векторы a, b, c единичной длины образуют попарно углы 60°. Найдите угол между векторами a и b-c:
а) 90°
б) 40°
в) 60°
Точка О, являющаяся центром масс тетраэдра, делит все отрезки, соединяющие вершины тетраэдра с центрами масс противоположных граней в отношении:
а) 4 : 1
б) 2 : 1
в) 3 : 1
Даны три точки A(1;0;1), B(-1;1;2), C(0;2;-1). Найдите на оси z такую точку D(0;0;c), чтобы векторы AB и CD были перпендикулярны:
а) 1
б) -1
в) 0
Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 1. Объем параллелепипеда равен 5. Найдите высоту цилиндра:
а) 1,5
б) 1,25
в) 1,20
Найдите D(x,y,z), если сумма векторов AB и CD равна нулю. A(1;0;1), B(-1;1;2), C(0;2;-1):
а) D(-2;1;2)
б) D(1;2;-2)
в) D(2;1;-2) +
В цилиндрическом сосуде уровень жидкости достигает 27 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в 3 раза больше первого:
а) 9 см
б) 3 см
в) 6 см
Образующая конуса наклонена к плоскости основания под углом 60°. Радиус основания r. Вычислить боковую поверхность конуса:
а) 4π²
б) π²
в) 2π²
В цилиндрический сосуд налили 1200 см³ воды. Уровень воды при этом достигает высоты 12 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 10 см. Чему равен объем детали:
а) 1100 см³
б) 1000 см³
в) 100 см³
Куча щебня имеет коническую форму, радиус основания которой 2 м и образующая 3,5 м. Сколько надо возов, чтобы перевезти щебень, уложенный в кучу:
а) 72
б) 63
в) 85
Пусть V, r, h соответственно объем, радиус и высота цилиндра. Найдите объем, если r=2√2 cм, h=3 см:
а) 43π см³
б) 24π см³
в) 31π см³
Жидкость, налитая в конический сосуд, имеющий 0,18 м высоты и 0,24 м в диаметре основания, переливается в цилиндрический сосуд, диаметр основания которого 0,10 м. Как высоко будет уровень жидкости в сосуде:
а) 1,4 м
б) 2,7 м
в) 0,35 м
Радиус основания цилиндра равен 7, а высота — 10. Найдите площадь боковой поверхности цилиндра, деленную на π:
а) 124
б) 140
в) 104
Длина окружности основания конуса равна 5, образующая равна 8. Найдите площадь боковой поверхности конуса:
а) 32
б) 10
в) 20
Шар вписан в цилиндр. Площадь поверхности шара равна 41. Найдите площадь полной поверхности цилиндра:
а) 65
б) 61,5
в) 60
Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 9 раз:
а) в 9 раз
б) в 11 раз
в) в 5 раз
Площадь боковой поверхности цилиндра равна 18π, а диаметр основания равен 9. Найдите высоту цилиндра:
а) 3
б) 4
в) 2
Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания:
а) 60°
б) 80°
в) 30°
Площадь полной поверхности конуса равна 148. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса:
а) 30
б) 37
в) 29
Нормы оценок:
«2» 0-7
«3» 8-15
«4» 16-25
«5» 26-30










 Рис.2 М
Рис.2 М
 Д Рис. 1
Д Рис. 1