Российская Федерация, Красные Баки
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Был в сети 25.08.2024 17:45
Сперанский Дмитрий Николаевич
Учитель математики
57 лет
866
67 208 
Местоположение
Специализация
Геометрия 10 класс
Категория:
Геометрия
19.07.2018 11:26
Просмотр содержимого документа
«Геометрия 10 класс»
ГЕОМЕТРИЯ 10 КЛАСС
Правильные
многогранники
Л.С. Атанасян. Геометрия 10-11.
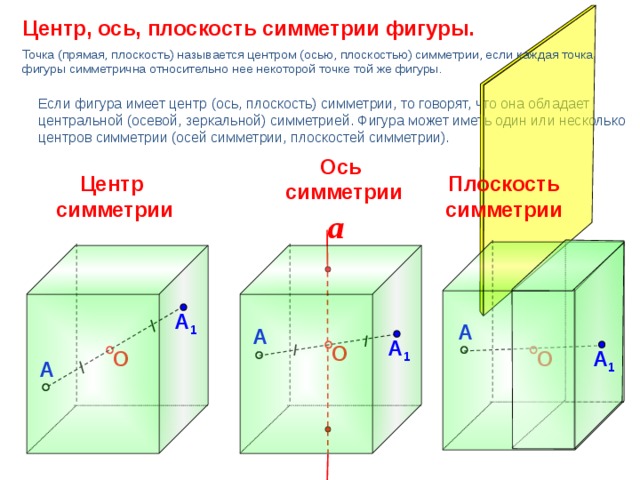
Центр, ось, плоскость симметрии фигуры.
Точка (прямая, плоскость) называется центром (осью, плоскостью) симметрии, если каждая точка фигуры симметрична относительно нее некоторой точке той же фигуры.
Если фигура имеет центр (ось, плоскость) симметрии, то говорят, что она обладает центральной (осевой, зеркальной) симметрией. Фигура может иметь один или несколько центров симметрии (осей симметрии, плоскостей симметрии).
Ось
симметрии
Центр
Плоскость симметрии
симметрии
a
А 1
«Геометрия 10-11» Л.С. Атанасян и др.
А
А
А 1
О
О
А 1
О
А
3
Мы различаем правильный тетраэдр
и правильную пирамиду.
В отличие от правильного тетраэдра, все ребра которого равны, в правильной треугольной пирамиде боковые ребра равны друг другу,
но они могут быть не равны ребрам основания пирамиды.
«Геометрия 10-11» Л.С. Атанасян и др.
Названия многогранников пришли из Древней Греции и в них указывается число граней.
«тетра» - 4
4
Элементы симметрии тетраэдра.
Правильный тетраэдр не имеет центра симметрии.
Осей симметрии – 3. Плоскостей симметрии – 6.
Прямая, проходящая через середины двух противоположных ребер, является его осью симметрии. Плоскость, проходящая через ребро перпендикулярно к противоположному ребру, - ось симметрии.
«Геометрия 10-11» Л.С. Атанасян и др.
4
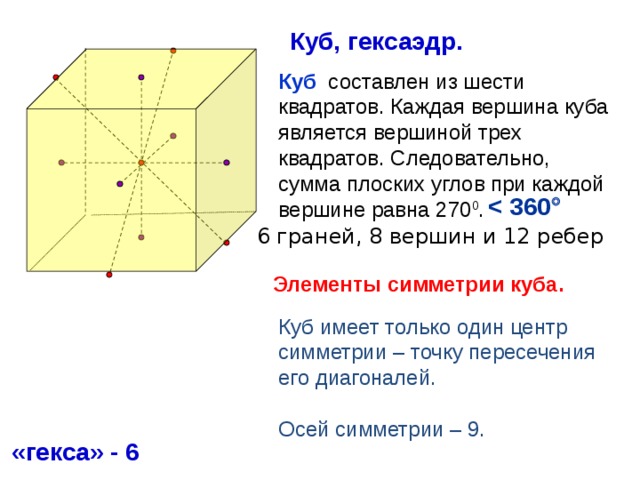
Куб, гексаэдр.
Куб составлен из шести квадратов. Каждая вершина куба является вершиной трех квадратов. Следовательно, сумма плоских углов при каждой вершине равна 270 0 .
6 граней, 8 вершин и 12 ребер
Элементы симметрии куба.
«Геометрия 10-11» Л.С. Атанасян и др.
Куб имеет только один центр симметрии – точку пересечения его диагоналей.
Осей симметрии – 9.
«гекса» - 6
6
Куб имеет 9 плоскостей симметрии.
«Геометрия 10-11» Л.С. Атанасян и др.
6
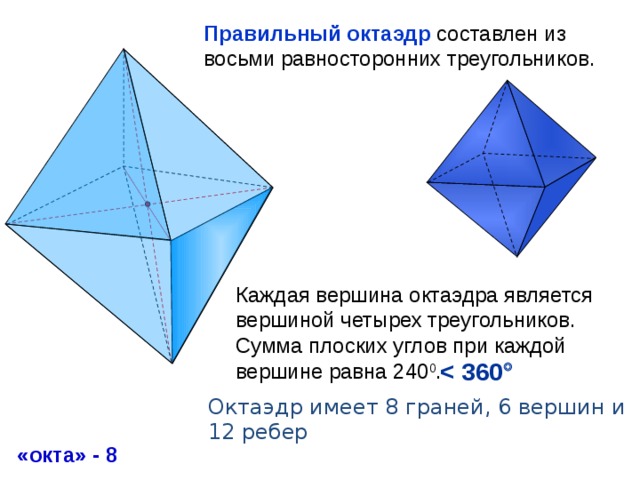
Правильный октаэдр составлен из восьми равносторонних треугольников.
Каждая вершина октаэдра является вершиной четырех треугольников. Сумма плоских углов при каждой вершине равна 240 0 .
«Геометрия 10-11» Л.С. Атанасян и др.
Октаэдр имеет 8 граней, 6 вершин и
12 ребер
«окта» - 8
6
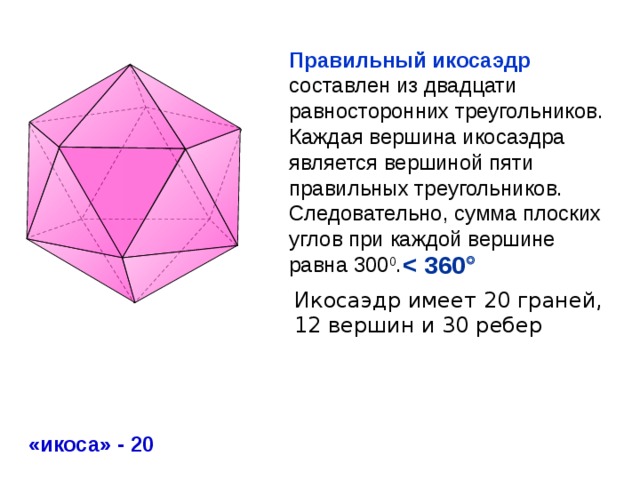
Правильный икосаэдр составлен из двадцати равносторонних треугольников. Каждая вершина икосаэдра является вершиной пяти правильных треугольников. Следовательно, сумма плоских углов при каждой вершине равна 300 0 .
Икосаэдр имеет 20 граней,
12 вершин и 30 ребер
«Геометрия 10-11» Л.С. Атанасян и др.
«икоса» - 20
9
Правильный додекаэдр составлен из двенадцати правильных шестиугольников. Каждая вершина додекаэдра является вершиной трех правильных пятиугольников. Следовательно, сумма плоских углов при каждой вершине равна 324 0 .
Додекаэдр имеет 12 граней,
20 вершин и 30 ребер.
«Геометрия 10-11» Л.С. Атанасян и др.
«додека» - 12
9
Взаимное расположение прямых и плоскостей в пространстве
Две прямые
Две плоскости
Прямая и плоскость
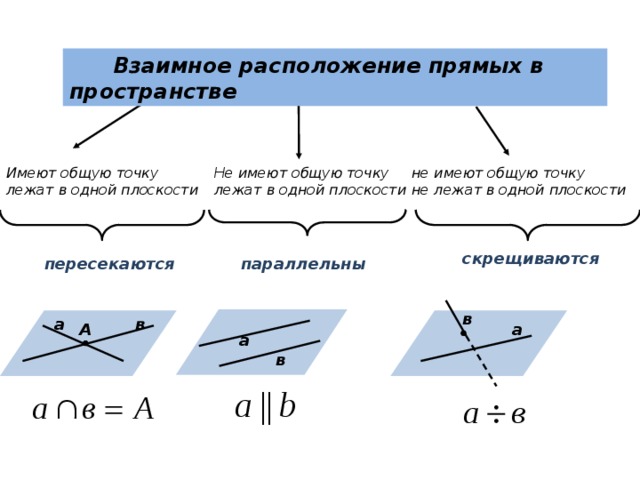
Взаимное расположение прямых в пространстве
Имеют общую точку
Не имеют общую точку
не имеют общую точку
лежат в одной плоскости
не лежат в одной плоскости
лежат в одной плоскости
скрещиваются
параллельны
пересекаются
в
в
а
а
А
а
в
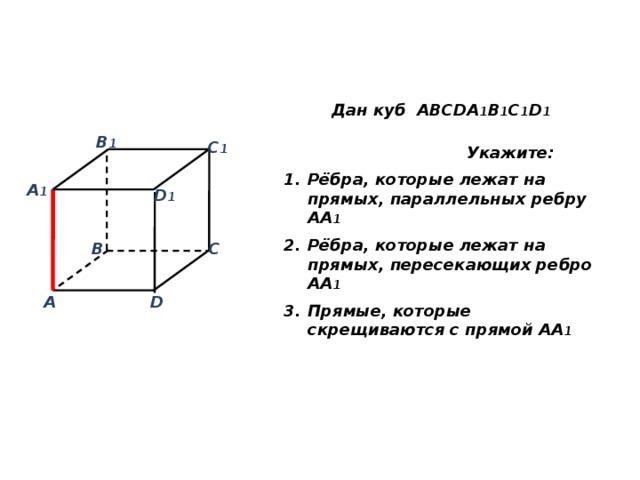
Дан куб ABCDA 1 B 1 C 1 D 1
B 1
C 1
Укажите:
- Рёбра, которые лежат на прямых, параллельных ребру АА 1
- Рёбра, которые лежат на прямых, пересекающих ребро АА 1
- Прямые, которые скрещиваются с прямой АА 1
А 1
D 1
B
C
А
D
Дана пирамида ABCD Укажите:
1.плоскости, в которых лежат прямые РЕ, МК, DB, АВ, ЕС;
2.точки пересечения прямой DK с плоскостью ABC, прямой СЕ с плоскостью ADB;
3. точки, лежащие в плоскостях ADB и DBC;
4.прямые, по которым пересекаются плоскости ABC и DCB, ABD и CDA, PDC и ABC.
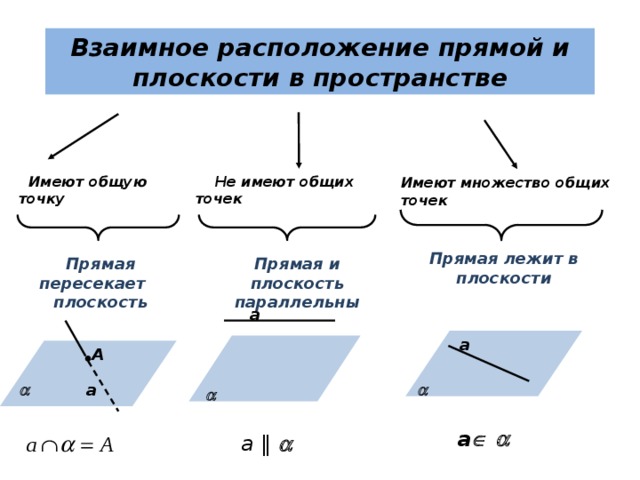
Взаимное расположение прямой и плоскости в пространстве
Не имеют общих точек
Имеют общую точку
Имеют множество общих точек
Прямая лежит в плоскости
Прямая пересекает плоскость
Прямая и плоскость параллельны
а
а
А
а
а
а ‖
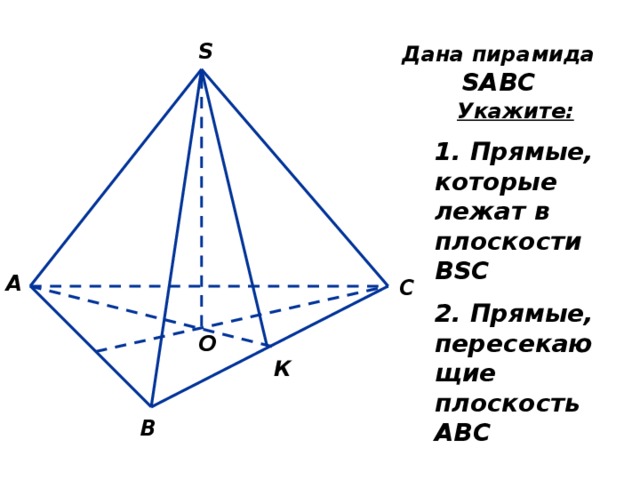
S
Дана пирамида SABC
Укажите:
1. Прямые, которые лежат в плоскости BSC
2. Прямые, пересекающие плоскость АВС
А
С
О
К
В
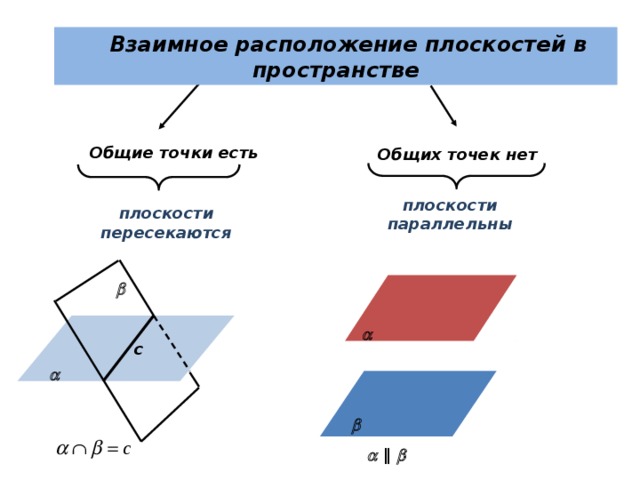
Взаимное расположение плоскостей в пространстве
Общие точки есть
Общих точек нет
плоскости параллельны
плоскости пересекаются
с
‖
Угол между прямой и плоскостью.
Угол между плоскостями.
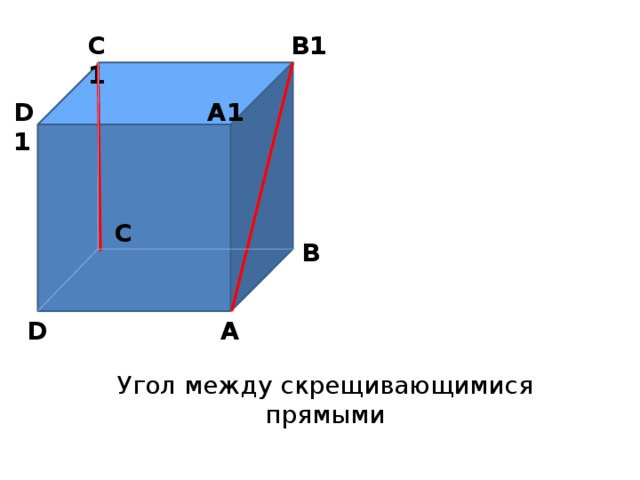
B1
C1
A1
D1
C
B
A
D
Угол между скрещивающимися прямыми
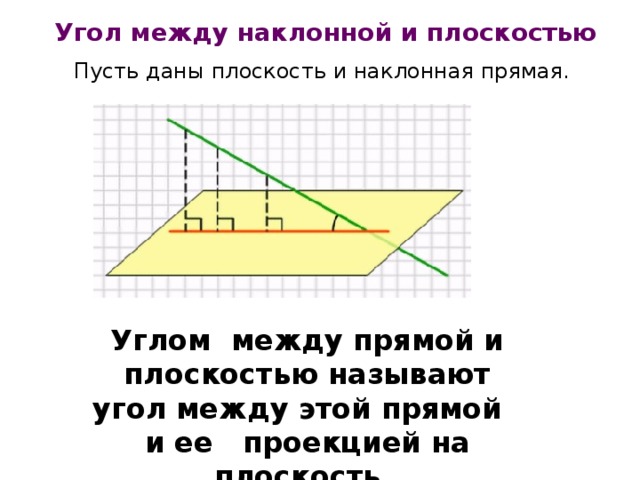
Угол между наклонной и плоскостью
Пусть даны плоскость и наклонная прямая.
Углом между прямой и плоскостью называют угол между этой прямой и ее проекцией на плоскость.
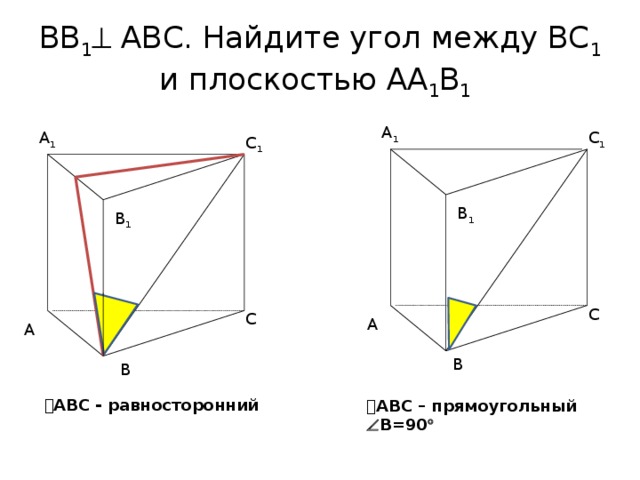
ВВ 1 АВС. Найдите угол между ВС 1 и плоскостью АА 1 В 1
А 1
А 1
С 1
С 1
В 1
В 1
С
С
А
А
В
В
АВС - равносторонний
АВС – прямоугольный В=90
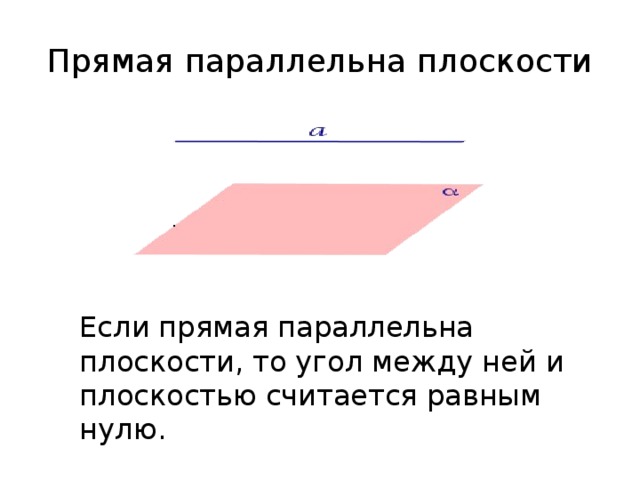
Прямая параллельна плоскости
.
Если прямая параллельна плоскости, то угол между ней и плоскостью считается равным нулю.
Прямая перпендикулярна к плоскости
а
O
Если а , то угол = 90
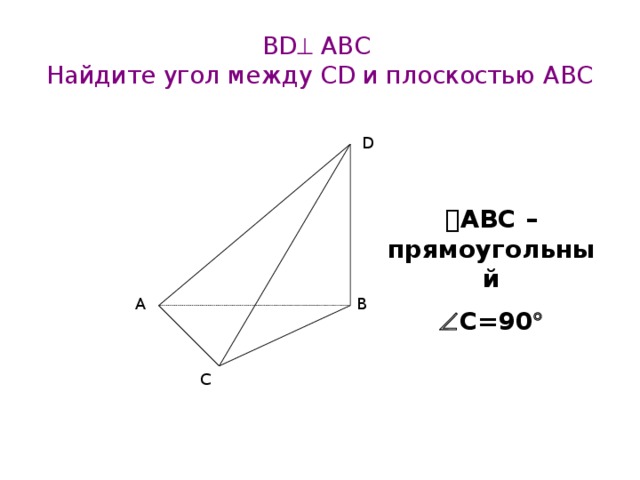
BD АВС Найдите угол между CD и плоскостью ABС
D
АВС – прямоугольный
C=90
А
B
C
УГОЛ МЕЖДУ ПЛОСКОСТЯМИ
(ДВУГРАННЫЙ УГОЛ)
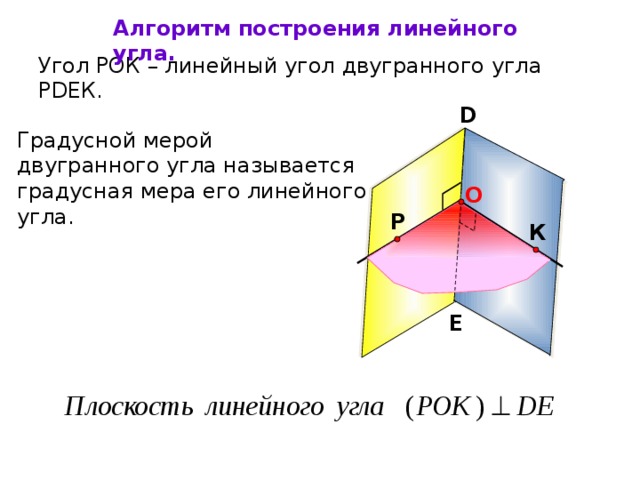
Алгоритм построения линейного угла.
Угол РОК – линейный угол двугранного угла РDEК.
D
Градусной мерой двугранного угла называется градусная мера его линейного угла.
O
Р
К
E
Двугранный угол может быть прямым, острым, тупым
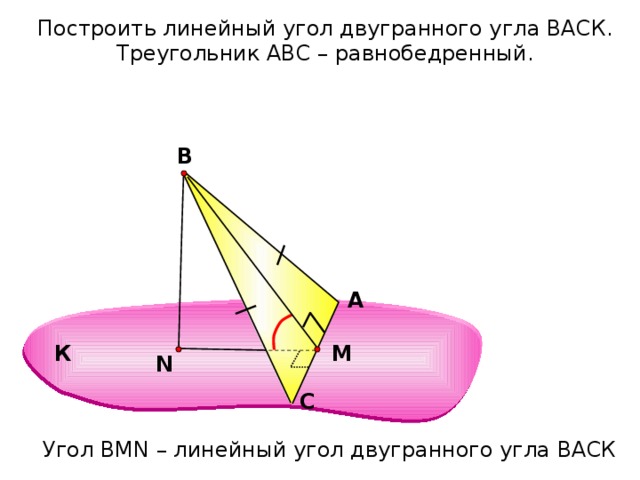
Построить линейный угол двугранного угла ВАСК.
Треугольник АВС – равнобедренный.
В
А
К
M
N
С
Угол ВMN – линейный угол двугранного угла ВАСК
28
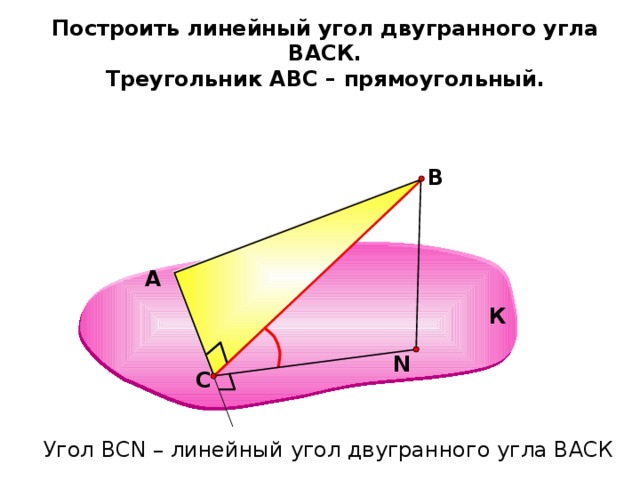
Построить линейный угол двугранного угла ВАСК.
Треугольник АВС – прямоугольный.
В
А
К
N
С
Угол ВСN – линейный угол двугранного угла ВАСК
29
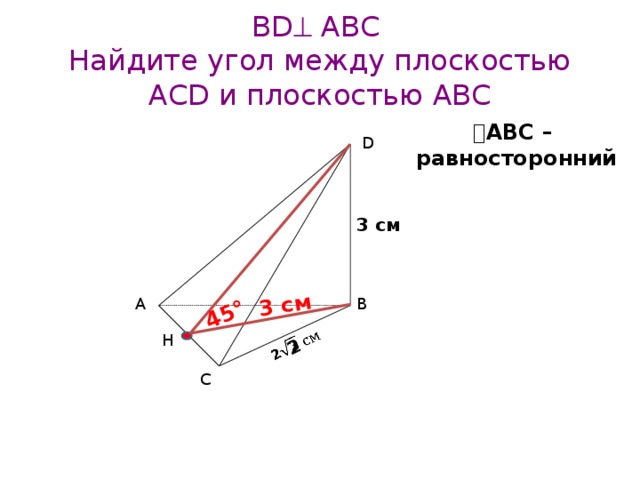
2
3 см
45°
BD АВС Найдите угол между плоскостью АCD и плоскостью ABС
АВС – равносторонний
D
3 см
B
А
Н
C
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
