Просмотр содержимого документа
«Касательная к окружности»

ТЕМА: Касательная к окружности.
Рассмотреть различные случаи взаимного расположения прямой и окружности, ввести понятие касательной, рассмотреть её свойства и признак, а также свойство отрезков касательных, проведённых из одной точки.
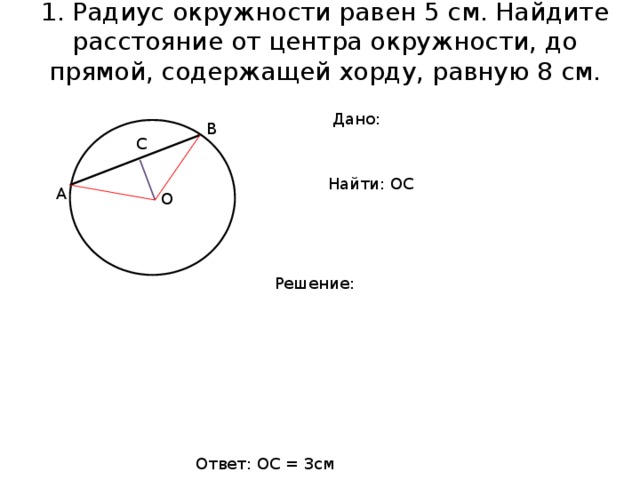
1. Радиус окружности равен 5 см. Найдите расстояние от центра окружности, до прямой, содержащей хорду, равную 8 см.
Дано:
В
ОО
С
Найти: ОС
А
О
Решение:
Ответ: ОС = 3см

2. Найдите расстояние от точки А до ближайшей к ней точки окружности с центром О радиуса r, если а)ОА = 12см, r = 8см; б) ОА = 6см, r = 8см
 r Вывод : Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек. d r " width="640"
r Вывод : Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек. d r " width="640"
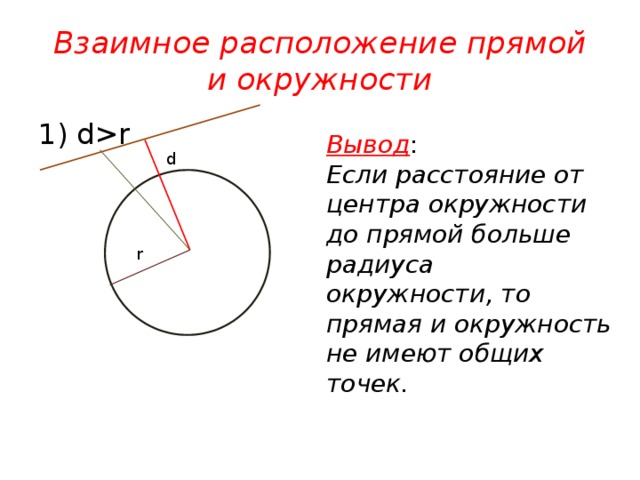
Взаимное расположение прямой и окружности
1) dr
Вывод :
Если расстояние от центра окружности до прямой больше радиуса
окружности, то прямая и окружность не имеют общих точек.
d
r
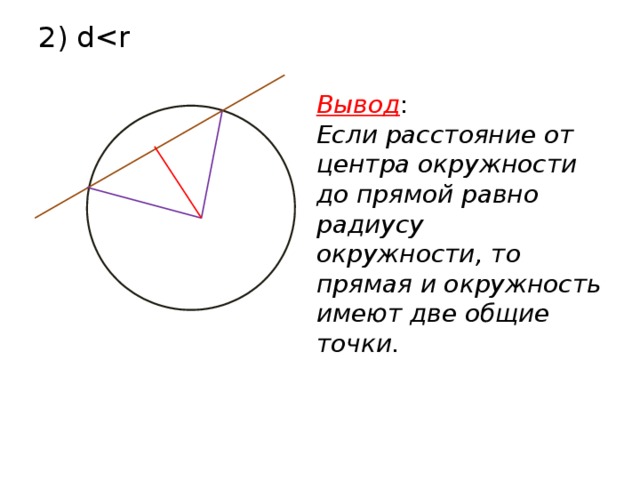
2) d
Вывод :
Если расстояние от центра окружности до прямой равно радиусу
окружности, то прямая и окружность имеют две общие точки.
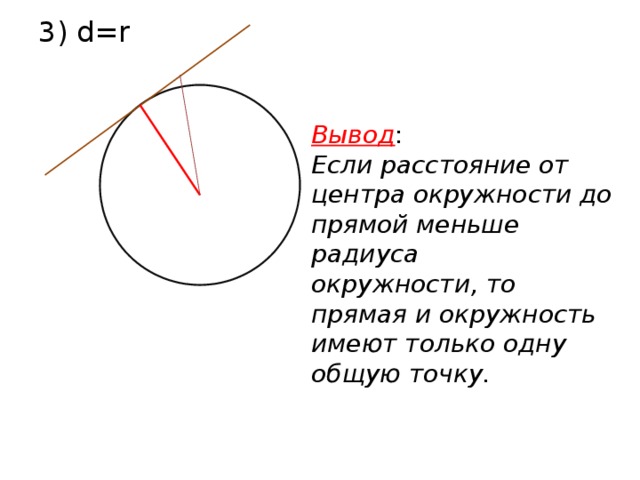
3) d=r
Вывод :
Если расстояние от центра окружности до прямой меньше радиуса
окружности, то прямая и окружность имеют только одну общую точку.

Решаем: 631(а, г, д) устно, 632
- Дома: п.68; №631(б, в), 633.








 r Вывод : Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек. d r " width="640"
r Вывод : Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек. d r " width="640"













