Тема: Иррациональные уравнения.
Цель работы:
- повторить понятия: равносильные уравнения, их свойства, потеря корней, посторонние корни, иррациональные уравнения;
- развитие умений и навыков работы с источником информации, с практическим материалом.
Основной теоретический материал:
1) Ш.А. Алимов. Алгебра и начала математического анализа 10-11 класс, глава 2, §8-9.
2) Способы решения:
Просмотр содержимого документа
«Конспект урока: "Иррациональные уравнения"»
Тема: Иррациональные уравнения.
Цель работы:
повторить понятия: равносильные уравнения, их свойства, потеря корней, посторонние корни, иррациональные уравнения;
развитие умений и навыков работы с источником информации, с практическим материалом.
Основной теоретический материал:
1) Ш.А. Алимов. Алгебра и начала математического анализа 10-11 класс, глава 2, §8-9.
2) Способы решения:
Уединение радикала и возведение в степень.
Смысл таких преобразований в сведении данного иррационального уравнения к равносильному ему рациональному уравнению.
Уравнения, содержащие кубические радикалы.
Основным методом решения уравнений является последовательное возведение в куб обеих частей уравнения, используя формулы
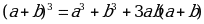 ,
, 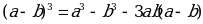 .
.
Задание:
1) Перепишите и заполните пропуски:
Пример 1. Решить уравнение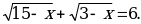 Решение: Уединим радикал
Решение: Уединим радикал 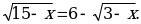 Это уравнение равносильно системе
Это уравнение равносильно системе  Решим уравнение (1):
Решим уравнение (1): 

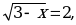
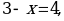 х = … Найденное значение
х = … Найденное значение  удовлетворяет условиям (2) и (3).
удовлетворяет условиям (2) и (3).
Ответ: –1. Пример 2. а) Найдите корень уравнения 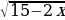 = 3 . Решение: Возведем в квадрат правую и левую части уравнения:
= 3 . Решение: Возведем в квадрат правую и левую части уравнения:
 )2 = 32, 15 – 2х = 9,
)2 = 32, 15 – 2х = 9,
–2х = 9 – 15, –2х = – 6, х = ... Сделаем проверку. Для этого подставим число 3 в исходное уравнение: 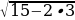 = 3, 3 = 3 – верно.
= 3, 3 = 3 – верно.
Ответ: 3.
б) Решить уравнение 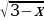 =
=  .
.
Решение: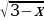 =
=  =
=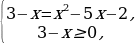 ˂=
˂= 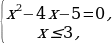 =
= 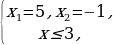 = х = ...
= х = ...
Ответ: – 1.
Пример 3. Решить уравнение  = х -7 .
= х -7 .
Решение: = х -7 =
= х -7 =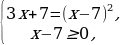 =
=  =
= 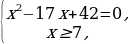 =
= 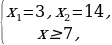 = х = ...
= х = ...
Ответ: 14.
Пример 4. Решите уравнение 
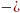
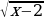 =
=  .
.
Решение:
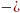
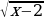 =
=  = 7
= 7 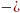 х + х
х + х 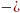 2
2 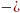 2
2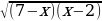 = 2х
= 2х 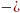 5 =
5 = 5 – х =
5 – х = 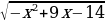 =
= 25 – 10х + х2 =
25 – 10х + х2 = 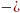 х2 + 9х – 14 =
х2 + 9х – 14 = 2х2
2х2 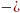 19х + 39 = 0,
19х + 39 = 0,
D = (– 19)2 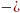 4
4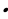 2
2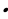 39= 361 – 312 = …, х1= (19 + 7) : 4 = …, х2 = (19 – 7) : 4 = …,
39= 361 – 312 = …, х1= (19 + 7) : 4 = …, х2 = (19 – 7) : 4 = …,
Проверка: а) х1= 6,5, 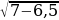 –
– 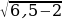 =
=  ,
,

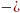
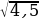 =
= 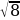 – неверное равенство.
– неверное равенство.
б) х2 = 3, 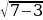 –
– 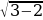 =
= 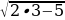 ,
, 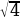
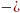
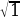 =
= 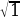 , – верное равенство. Ответ: 3.
, – верное равенство. Ответ: 3.
Пример 5. Решить уравнение 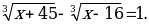
Решение: Возводим в куб обе части уравнения  получим
получим 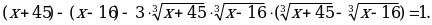 Учитывая, что выражение в скобках равно 1 (см. условие), получаем
Учитывая, что выражение в скобках равно 1 (см. условие), получаем 
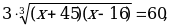
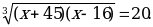 Возводим в куб:
Возводим в куб: 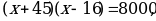
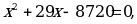
 Проверкой убеждаемся, что
Проверкой убеждаемся, что 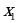 и
и 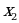 корни уравнения.
корни уравнения.
Ответ: 80, – 109.
2)Решить задание ( по примерам):
Решить уравнения:
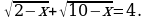
а) 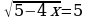 . б)
. б) 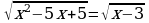 .
.
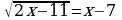 .
.

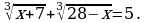







 Решим уравнение (1):
Решим уравнение (1): 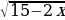 = 3 . Решение: Возведем в квадрат правую и левую части уравнения:
= 3 . Решение: Возведем в квадрат правую и левую части уравнения: )2 = 32, 15 – 2х = 9,
)2 = 32, 15 – 2х = 9, 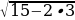 = 3, 3 = 3 – верно.
= 3, 3 = 3 – верно. 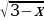 =
=  .
. 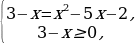 ˂=
˂= 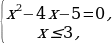 =
= 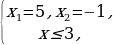 = х = ...
= х = ...  = х -7 .
= х -7 . 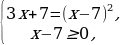 =
=  =
= 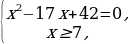 =
= 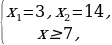 = х = ...
= х = ... 
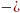
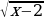 =
=  .
.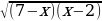 = 2х
= 2х  5 – х =
5 – х = 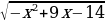 =
=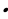 2
2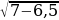 –
– 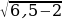 =
=  ,
,
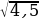 =
= 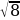 – неверное равенство.
– неверное равенство.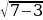 –
– 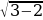 =
= 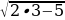 ,
, 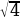
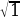 =
=  Проверкой убеждаемся, что
Проверкой убеждаемся, что 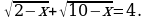
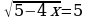 . б)
. б) 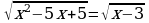 .
. 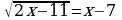 .
.