преподаватель: Белова Н.В.
Дата:
Предмет: математика
Тема урока: Степень с действительным показателем.
Цели:
Образовательные:
обобщить понятие степени;
отработать умение находить значение степени с действительным показателем;
закрепить умения использовать свойства степени при упрощении выражений;
выработать навык использования свойств степени при вычислениях.
Развивающие:
интеллектуальное, эмоциональное, личностное развитие ученика;
развивать умение обобщать, систематизировать на основе сравнения, делать вывод;
активизировать самостоятельную деятельность;
развивать познавательный интерес.
Воспитательные:
воспитание коммуникативной и информационной культуры обучающихся;
эстетическое воспитание осуществляется через формирование умения рационально, аккуратно оформлять задание на доске и в тетради.
Учащиеся должны знать: определение и свойства степени с действительным показателем
Учащиеся должны уметь: использовать свойства степени при вычислениях и упрощении выражений;
решать примеры, содержащие степень; сравнивать, находить сходства и отличия.
Форма урока: семинар – практикум, с элементами исследования.
Компьютерная поддержка.
Форма организации обучения: индивидуальная, групповая.
Педагогические технологии: проблемное обучение, обучение в сотрудничестве, личностно - ориентированное обучение, коммуникативное.
Тип урока: урок исследовательской и практической работы.
Место урока в теме: урок комплексного применения знаний и умений (урок закрепления).
Наглядность к уроку и раздаточный материал: презентация, формулы и таблицы; задание для самостоятельной работы, листы самоконтроля.
Ход урока
I. Организационный этап (2 мин) До начала урока дежурные раздают раздаточный материал.
Приветствие детей. Проверка готовности к уроку. (слайд 1)
Заполнение журнала (кто отсутствует?)
Перед детьми листы самоконтроля, которые они заполняют в течении урока.
II. Повторение теоретического материала по теме. Актуализация знаний (6 мин) (слайд 2)
Учитель просит учащихся дать определение степени с натуральным показателем.
Звучит определение.
Определение. Степенью действительного числа а с натуральным показателем п называется произведение п множителей, каждый из которых равен а.
Учитель просит учащихся дать определение степени с целым показателем.
Звучит определение.
Определение. Если 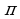 - целое отрицательное число, то
- целое отрицательное число, то 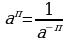 , где
, где 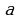
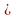 0 Учитель спрашивает: «Чему равна нулевая, первая степень любого действительного числа?»
0 Учитель спрашивает: «Чему равна нулевая, первая степень любого действительного числа?» 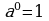 ;
; 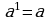 .
.
Учитель просит учащихся дать определение степени с рациональным
показателем. Звучит определение.
Определение. Степенью действительного числа а 0 c рациональным показателем r = 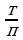 , где m- целое, n- натуральное, называется число
, где m- целое, n- натуральное, называется число 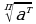 :
:
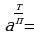
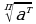 . Если
. Если 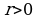 , то
, то 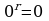 .
.
Учитель: «Вспомните основные свойства степени».
Учащиеся перечисляют свойства степени:
Для любых действительных чисел т и п и для любых положительных а и в выполняются равенства:
1. 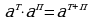 4.
4. 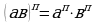
2. 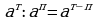 5.
5.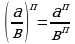
3. 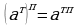
Во время ответов на интерактивной доске учащиеся видят определения и свойства степени, и если надо вносят дополнения и исправления в ответы своих товарищей.
Устная работа по решению простейших задач по теме « Основные свойства степени» (слайд 3)
Учитель предлагает учащимся применить только что сформулированные теоретические факты к решению упражнений.
Вычислите:
1) 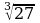
2) 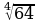 4)
4) 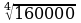
3) 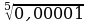 5)
5) 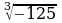
Упростите:
1) 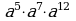 4)
4) 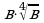
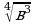
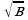
2)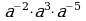 5)
5) 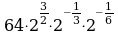
3) (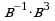 )
)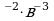 6)
6) 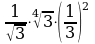
III. Определение темы урока (групповая работа). Мотивация учебной деятельности учащихся. (5 мин)
Каждому ряду даются карточки с заданиями:
I ряд: 75; 252; -3*(-2)5 ; 7*52; (7*5)2; 592-362; 36*(3/6) 2;
II ряд: (4*5) -2; -5*25; (6-8)5; 2 2-43; -6 -2-(-1)14; 10-5*24
III ряд: 4-2; (1/7) -2; (-1)9/7; 8*4-3/2; 18*(-9)-1/2; 25-20180
Что объединяет все эти задания, чем они схожи?
(Все задания на нахождение степени) Пишу на доске первое слово темы…
А чем они отличаются?
( 1ряд -натуральные; 2ряд-целые,3 ряд-рациональные)
Все они вместе образуют класс действительных чисел.
М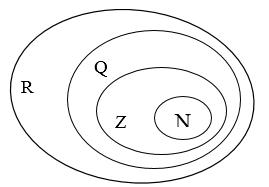 ножество всех действительных чисел записывают в виде кругов Леонардо Эйлера (швейцария):
ножество всех действительных чисел записывают в виде кругов Леонардо Эйлера (швейцария):
· N — множество натуральных
чисел,
· Z — множество целых
чисел,
· Q — множество рациональных чисел,
· R — множество всех
действительных чисел.
Историческая справка (слайд 4)
Понятие степени с натуральным показателем сформировалось ещё у древних народов. Квадрат и куб числа использовались для вычисления площадей и объемов. Степени некоторых чисел использовались при решении отдельных задач учеными Древнего Египта и Вавилона.
В III веке вышла книга греческого ученого Диофанта “Арифметика”, в которой было положено начало введению буквенной символики. Диофант вводит символы для первых шести степеней неизвестного и обратных им величин. В этой книге квадрат обозначается знаком и индексом; например, куб – знаком k c индексом r и т.д. (слайд 5)
Большой вклад в развитие понятия степени внес древнегреческий ученый Пифагор. У него была целая школа, и всех его учеников называли пифагорейцами. Они придумали, что каждое число можно представить в виде фигур. Например, числа 4, 9 и 16 они представляли в виде квадратов.
(слайд 6)
Вавилоняне пошли дальше: составляли и пользовались таблицами квадратов и кубов чисел. (слайд 7)
XVI век. В этом веке понятие степени расширилось: его стали относить не только к конкретному числу, но и к переменной. Как тогда говорили «к числам вообще». Английский математик С. Стевин придумал запись для обозначения степени: запись 3(3)+5(2)–4 обозначала такую современную запись 33 + 52 – 4. (слайд 8)
Позже дробные и отрицательные, показатели встречаются в “Полной арифметике” (1544 г.) немецкого математика М.Штифеля и у С. Стевина.
С.Стевин предположил подразумевать под степенью с показателем вида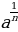 корень, т.е.
корень, т.е. 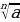 . (слайд 9)
. (слайд 9)
В конце ХVI века Франсуа Виет ввел буквы для обозначения не только переменных, но и их коэффициентов. Он применял сокращения: N, Q, C – для первой, второй и третьей степеней.
Но современные обозначения (типа 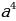 ,
, 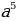 ) в XVII веке ввел Рене Декарт. (слайд 10)
) в XVII веке ввел Рене Декарт. (слайд 10)
Современные определения и обозначения степени с нулевым, отрицательным и дробным показателем берут начало от работ английских математиков Джона Валлиса(1616–1703) и Исаака Ньютона.
IV. Первичное закрепление (20 мин) (слайд 11)
1. Учащиеся у доски - разбор упражнений из учебника(Алимов Ш.А.): № 74, № 77, № 82(а; б; в).
Решение:
№74:
а) 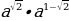 =
= 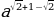 = a;
= a;
б)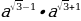 =
= 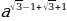 =
= 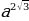 ;
;
в) 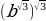 :
: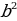 =
= 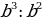 =
= 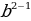 = b.
= b.
№ 77:
а) 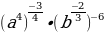 =
= 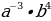 =
= 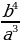 ;
;
б) 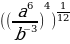 =
= 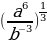 =
= 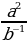 =
= 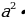 b.
b.
№82:
а) 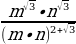 =
= 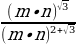 =
= 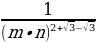 =
=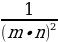 ;
;
б) 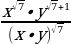 =
=  = y;
= y;
в) (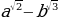 )
)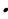 (
(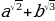 ) =
) =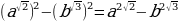 .
.
2. Разноуровневая самостоятельная работа «Повышение вычислительной культуры»:
Вариант 1
Вычислите:
| Уровень I | ответ |
| (-2)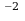 | 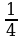 |
| 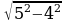
| 3 |
| 27 3 3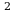 | 1 |
| (6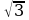 ) )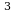 | 648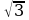 |
| 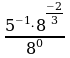
| 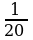
|
| Уровень II |
|
| 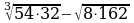
| -24 |
| 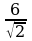
|
3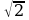 |
| (2-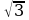 ) )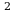 | 7- 4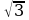 |
| -0,064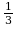 0,49 0,49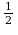 |
-0,28 |
| Уровень III |
|
| 36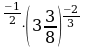 | 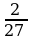
|
| 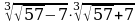
| 2 |
| 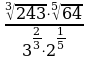
|
6 |
Вариант 2
Вычислите:
| Уровень I | ответ |
| (-3)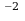 | 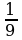
|
| 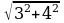
| 5 |
| 4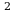 64 64 | 1 |
| (7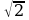 ) )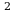 | 98 |
| 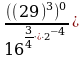
| 2 |
| Уровень II |
|
| (-2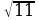 ) )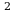 | 44 |
| 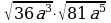 при а =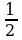 |
3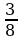 |
| 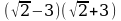
| -7 |
| 125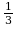 16 16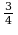 -36 -36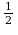 |
34 |
| Уровень III |
|
| 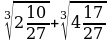
|
3 |
| 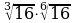
| 4 |
| 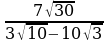 + +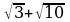
|
0 |
(слайд12)проверка
Учащийся должен решить задания своего уровня сложности. Если у него остается ещё время, то он может набирать дополнительные баллы, решая задания другого уровня сложности. Сильные учащиеся, прорешав задания менее сложного уровня, смогут помочь своим товарищам из другой группы в случае необходимости. (По просьбе учителя они выступают в роли консультантов).
V. Творческое применение и добывание знаний в новой ситуации (исследовательская работа) (8мин)
Однажды, листая страницы сборника олимпиадных задач по математике, я увидела с первого взгляда очень трудную задачу, точнее сказать пример. Надо было найти последнюю цифру суммы 19811989 + 19821989 + 19831989 + 19841989 +19851989 +…+ 19891989. Потом я подумала, а ведь должен же быть, какой-нибудь рациональный способ вычисления. Мне стало интересно, есть ли какая-нибудь закономерность в том, как меняется последняя цифра степени натурального числа? (слайд13)
Для этого заполним таблицу:
| № /n | 1 | 2 | 3 | 4 | 5 | 6 | Вывод |
| 1 |
|
|
|
|
|
|
|
| 2 |
|
|
|
|
|
|
|
| 3 |
|
|
|
|
|
|
|
| 4 |
|
|
|
|
|
|
|
| 5 |
|
|
|
|
|
|
|
| 6 |
|
|
|
|
|
|
|
| 7 |
|
|
|
|
|
|
|
| 8 |
|
|
|
|
|
|
|
| 9 |
|
|
|
|
|
|
|
Образцы формулировки выводов:
Вседа повторяется…,Повторяется через…шагов
Я заполнила пятую строку, затем шестую и удивились. Оказывается, пятая степень числа оканчивается той же цифрой, что и первая степень числа; а шестая степень числа оканчивается той же цифрой, что и вторая степень этого числа; седьмая степень – что и третья степень этого числа. (слайд 14)
Заполняя таблицу выведем следующие закономерности изменения последней цифры степени натурального числа :
Во-первых, квадрат натурального числа может оканчиваться любой цифрой;
Во-вторых, куб натурального числа может оканчиваться любой цифрой;
В-третьих, четвертая степень натурального числа может оканчиваться одной из цифр: 0, 1, 5, 6;
В-четвертых, пятая степень натурального числа оканчивается той же цифрой, что и само число;
В-пятых, если запись натурального числа оканчивается на 1, на 5, на 6, то любая степень этого числа оканчивается соответственно на 1, на 5, на 6;
В-шестых, нечетные степени числа 4 оканчиваются цифрой 4, а четные - цифрой 6.
(слайд 15)
Задания:
Найдите последнюю цифру числа:
а)2100; ответ 6
б)54949; Последняя цифра числа 54949 совпадает с последней цифрой числа 949. Последние цифры степеней девятки чередуются так: 9, 1, 9, 1, 9, 1... То есть если показатель степени нечётный, степень оканчивается на 9. Значит, и число 949, и исходное число 54949 оканчиваются на 9.
2.В книге рекордов Гиннеса написано, что наибольшее известное простое число равно (23021337 − 1). Не опечатка ли это?
Любая степень числа, оканчивающегося цифрой 1, тоже оканчивается цифрой 1. Поэтому разность 23021377 – 1 оканчивается на 0 и, следовательно, не является простым числом. Ответ: Опечатка.
3.Делится ли число 4730+3950 на 10?
Число 4730 оканчивается цифрой 9, а число 3950 — цифрой 1 (это проверяется аналогично решению задачи 1). Значит, их сумма оканчивается на 0 и потому делится на 10.
(слайд 16)
VI. Домашнее задание (1мин):
Работа над ошибками.
Творческое задание: составить карточку с заданиями на применение свойств степеней для опроса на следующем уроке.
Повторить определение и свойства п. 34 учебника.
VII. Рефлексия (подведение итогов занятия) (3 мин)
Лист самоконтроля
| Вопросы теории | Задание у доски | Разноуровневая самостоятельная работа «Повышение вычислительной культуры» | Исследовательская работа | Итог |
|
|
|
|
|
|
(слайд 17)
Подсчет баллов :
Каждое задание в том числе и задание самостоятельной работы, если
оно выполнено верно, оценивается в 1 балл.
Заполнение листа самоконтроля
«5» - 15 баллов
«4» - 10 баллов
«3» - 7 баллов
…мы надеемся, что ты очень старался,
просто сегодня – не твой день!..
Решения самостоятельной работы учащиеся забирают с собой, чтобы дома сделать работу над ошибками, листы самоконтроля сдают учителю.
Выставление оценок.
(слайд 18)
После озвучивания оценок, дити выбирают одно из выссказываний на слайде и заканчиваеют его.
(слайд 19)
Резерв (дети решают кроссворд)







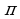 - целое отрицательное число, то
- целое отрицательное число, то 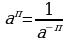 , где
, где 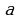
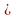 0 Учитель спрашивает: «Чему равна нулевая, первая степень любого действительного числа?»
0 Учитель спрашивает: «Чему равна нулевая, первая степень любого действительного числа?» 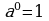 ;
; 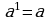 .
.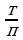 , где m- целое, n- натуральное, называется число
, где m- целое, n- натуральное, называется число 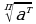 :
: 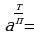
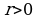 , то
, то 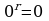 .
.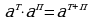 4.
4. 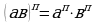
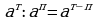 5.
5.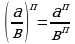
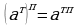
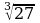
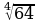 4)
4) 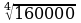
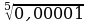 5)
5) 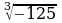
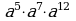 4)
4) 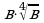
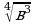
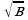
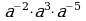 5)
5) 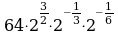
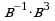 )
)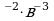 6)
6) 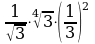
 ножество всех действительных чисел записывают в виде кругов Леонардо Эйлера (швейцария):
ножество всех действительных чисел записывают в виде кругов Леонардо Эйлера (швейцария):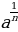 корень, т.е.
корень, т.е. 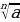 . (слайд 9)
. (слайд 9)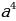 ,
, 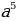 ) в XVII веке ввел Рене Декарт. (слайд 10)
) в XVII веке ввел Рене Декарт. (слайд 10)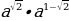 =
= 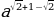 = a;
= a;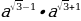 =
= 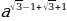 =
= 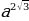 ;
;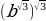 :
: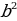 =
= 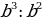 =
= 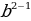 = b.
= b.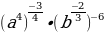 =
= 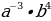 =
= 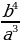 ;
;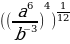 =
= 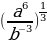 =
= 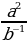 =
= 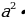 b.
b.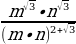 =
= 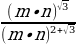 =
= 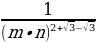 =
=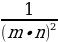 ;
;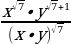 =
=  = y;
= y;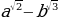 )
)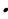 (
(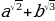 ) =
) =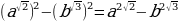 .
.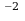
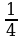
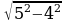
 3
3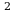
 )
)
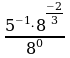
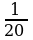
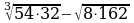
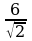
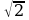
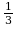 0,49
0,49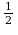
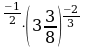
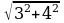
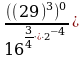
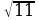 )
)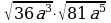
 -36
-36
 +
+