Государственное автономное профессиональное образовательное учреждение
Тюменской области
«Тюменский колледж транспортных технологий и сервиса»
Методическая разработка внеаудиторного занятия
| Дисциплина | Математика |
| Специальность СПО
группа | 23.02.06 Техническая эксплуатация подвижного состава железных дорог ТЭ-1-18 |
| Тема методической разработки | Математика в . . . |
| Продолжительность учебного занятия |
90 минут |
| Преподаватель | Шаркова Ольга Алексеевна |
Цель: выявление общих элементов и установление связи между математикой и другими предметами.
Задачи:
определить взаимосвязь математики и литературы, музыки, русского языка, иностранного языка;
способствовать формированию нового взгляда на мир;
формировать потребность поиска ответов на возникающие вопросы;
развивать творческие способности учащихся, ассоциативное мышление, воображение и фантазию.
воспитывать открытую, свободную личность, способную к познанию, активному действию.
Формы организации деятельности:
групповая работа;
фронтальная работа.
Тип занятия: урок - игра
Педагогическая технология (ее элементы): КСО
Методическое обеспечение: методическая разработка внеаудиторного занятия.
Средства обучения:
компьютер преподавателя;
презентация к уроку;
раздаточный материал.
Межпредметные связи: литература, музыка, русский язык, иностранный язык, история и т.д.
Ход мероприятия:
С тех пор, как существует мирозданье,
Такого нет, кто б не нуждался в знанье.
Какой мы не возьмем язык и век -
Всегда стремился к знанью человек…
Я рада приветствовать всех собравшихся.
Всем известно что «Математика — царица всех наук». Это изречение утверждает превосходство всевозможных формул и цифр.
Сегодня мы с вами проведем необычные уроки математики. Вы посмотрите на привычные вещи другими глазами.
Фокус «Угадаю день твоего рождения»
Запиши число твоего рождения
Умножь его на 2
К полученному числу припиши 0
К результату прибавь 73
Полученное число умножь на 5
Прибавьте номер месяца, в котором вы родились
Вычтете 365
Назовите полученный результат
Пример: 12*2=240+73=313*5=1565+7=1572-365=1207 (12 июля)
Физика
Связи между науками математики и физики многообразны и постоянны. Объектом чистой математики является весьма реальный материал: пространственные формы и количественные отношения материального мира. Тот факт, что этот материал принимает чрезвычайно абстрактную форму, может лишь слабо затушевать его происхождение из внешнего мира. Но чтобы быть в состоянии исследовать эти формы и отношения в чистом виде, необходимо совершено отделить их от их содержания, оставить это последнее в стороне, как нечто безразличное. Из этих соображений вытекает, что основным методом математики является метод абстракции. По способу отражения действительности она является аспектной наукой. Её предметной областью является вся действительность, другими словами, нет ни одной материальной области, в которой не проявились бы закономерности, изучаемые математикой. Таким образом, математика изучает количественные отношения и пространственные формы как существующих областей объектов, так и тех, которые можно «сконструировать».
Физика, как наука, имеет своей предметной области фундаментальные свойства материи в двух её формах - в форме вещества и поля. Они представляют собой комплекс самостоятельных областей знания, объединённых исходными принципами, фундаментальными теориями и методами исследования. В начале физика главным образом исследовала свойства окружающих нас тел.
Однако уже на этом этапе изучались и некоторые общие проблемы - движение, взаимодействие тел, строение вещества, природа и механизм ряда явлений, например тепловых, звуковых, оптических. Следовательно первоначально физика была в основном объектной наукой. Но в ХХ веке главным объектом физики становятся фундаментальные явления природы и описывающие их законы.
Математика как наука сформировалась первой, но по мере развития физических знаний математические методы находили всё большее применение в физических исследованиях.
Взаимосвязи математики и физики определяются прежде всего наличием общей предметной области, изучаемой ими, хотя и с различных точек зрения. Взаимосвязь математики и физики выражается во взаимодействии их идей и методов. Эти связи можно условно разделить на три вида, а именно:
1. Физика ставит задачи и создает необходимые для их решения математические идеи и методы, которые в дальнейшем служат базой для развития математической теории.
2. Развитая математическая теория с её идеями и математическим аппаратом используется для анализа физических явлений, что часто приводит к новой физической теории, которая в свою очередь приводит к развитию физической картины мира и возникновению новых физических проблем.
3. Развитие физической теории опирается на имеющийся определенный математический аппарат, но последний совершенствуется и развивается по мере его использования в физике.
Астрономия
"Астрономия (как наука) стала существовать с тех пор, как она соединилась с математикой"
А.И.Герцен
В XX веке астрономия разделилась на две главные ветви: наблюдательную и теоретическую. Наблюдательная астрономия — это получение наблюдательных данных о небесных телах, которые затем анализируются. Теоретическая астрономия ориентирована на разработку компьютерных, математических или аналитических моделей для описания астрономических объектов и явлений. Эти две ветви дополняют друг друга: теоретическая астрономия ищет объяснения результатам наблюдений, а наблюдательная астрономия даёт материал для теоретических выводов и гипотез и возможность их проверки.
В астрономии постоянно работают с математикой, главным образом, с системой координат. Расположение звезд на небе, составление карт. Запуски спутников и космических кораблей, любые виды прогноза основываются на применении различных систем координат. C помощью системы координат астрономы определяют расстояние до звёзд, их местоположение на карте звёздного неба. Размеры галактики, скорость её вращения, траектории движения планет и их размер.
Таким образом, можно сделать вывод о том, что движение звезд и планет, расположение звезд в небе - все это подчинено математическим правилам и законам. В основу астрономии положен математический аппарат, следовательно, без математики, такой предмет как астрономия, может и смог бы существовать, однако он не был бы тем, что мы имеем сегодня.
Биология
"Нет такого раздела математики,
пусть даже самого абстрактного, который
не может когда-либо быть применен к реальному миру."
Н.И.Лобачевский
Характерной чертой современных научных исследований является широкое применение точных математических методов в разнообразных областях знания. В последнее время математические методы проникают в экономику, лингвистику, психологию и многие другие области, а частности в биологические исследования и медицинскую диагностику. Проникновение математических методов в науку о живой природе идет сейчас по многим путям, с одной стороны — это использование современной вычислительной техники для быстрой и эффективной обработки биологической и медицинской информации, с другой - создание математических моделей, описывающих живые системы и происходящие в них процессы. Не менее важна и «обратная связь», возникающая между математикой и биологией: биология не только служит полем дли применения математических методов, но и становится все более существенным источником постановки новых математических задач.
Жизнь - одно из самых прекрасных и сложных явлений на планете, изучением которого с начала 20 века занимается далеко не одна биология. Физики, а затем и математики обнаружили ряд биологических явлений, которые можно описать на математическом языке. Николай Рашевский (один из наиболее ярких примеров его деятельности - создание в 1939 году первого научного журнала, посвящённому исследованиям в математической биологии) , Карл Людвиг фон Бертланфи (в 1938 году он сформулировал знаменитое уравнение роста, которое и по сей день применяется в рыбоводческих хозяйствах) и Алан Тьюринг (был одним из первых ученых кто применил компьютер для математического моделирования биологических задач) положили начало плодотворному союзу математического формализма и науки о жизни, а компьютеры позволили ученым проводить количественные исследования биологических явлений. Так родилась новая дисциплина - математическая биология, или биоматематика. Она внесла и продолжает вносить свой вклад в развитие биологии как посредством теоретического изучения динамических систем (мозга, муравейника или экосистем), так и благодаря решению практических задач в ходе изучения раковых заболеваний, эпидемий, СПИДа или свиного гриппа. Механизм обучения, запоминания букв, цифр и сигналов можно смоделировать с помощью нейронной сети. Модель памяти известна как сеть Хопфилда. Сегодня она используется в самых разных цифровых системах: не только для решения множества физических задач, но и в электронике, и при обработке изображений. Таким образом, можно сделать следующий вывод: в биологии математика является доминантным звеном.
География
В географии невозможно обойтись без математики. Одно из основных географических понятий – масштаб показывает, во сколько раз каждая линия, нанесенная на карту или чертёж, меньше или больше её действительных размеров. Помимо этого, в географии достаточно широко используется понятие математики, и главным образом статистики. К примеру - смертность. Смертность - статистический показатель, оценивающий количество смертей. В демографии отношение числа умерших к общему числу населения. Измеряется в промилле (‰). Соленость морей и океанов, также измеряют в промилле (отношение количества соли на литр воды). Географические координаты определяют положение точки на земной поверхности. Широта́ — угол между местным направлением зенита и плоскостью экватора, отсчитываемый от 0° до 90° в обе стороны от экватора. Таким образом мы можем наблюдать математические модели в географии, и сделать вывод о том, что без математики в географии невозможно было бы сделать прогноз погоды и даже, элементарно рассчитать широту и долготу. Поэтому, математика является в полной мере не слугой, а доминирующим звеном в географии.
Химия
Сама химия - это физика элементарных частиц, а в физике, как мы уже узнали, без математики никак нельзя обойтись. Есть огромное количество примеров где хорошо видно что без знания математики и элементарной логики в химии - делать нечего. Я перечислю только самые яркие из них: Как правильно рассчитать валентность в соединении серы или другого химического элемента имеющего переменную валентность с чем либо без математики? Как рассчитать процентную долю вещества в растворе без элементарного знания математики? Кристаллические решетки - это наиболее яркие примеры стереометрии в химии. Ведь свойства того или иного вещества во многом зависят от кристаллической решетки. Так, к примеру, и графит, и алмаз состоят из атомов углеродов, только алмаз, в отличие от графита невероятно прочный. В химии используются и декартовы координаты для построения в пространстве различных орбиталей. Цепочки превращений, это одно из наиболее распространенных химических заданий, которое без логики выполнить невозможно. Расчет распределения электронов по энергетическим уровням без знания математики невозможен... и так далее... Таким образом, можно сделать вывод о том, что математика в химии занимает доминирующую позицию.
Черчение
Как уже ранее говорилось, что масштаб показывает, во сколько раз каждая линия, нанесенная на карту или чертёж, меньше или больше её действительных размеров. Все черчение построено на строгой системе. Штриховка под углом 45 градусов, окружности, плоскость, проекции - все это математические понятия, без знания которых невозможно построить хоть один чертеж. Поэтому, математика и здесь, как мы можем видеть, занимает доминирующее положение.
Информатика
Одними их наиболее значимых примеров математики в информатике может послужить несколько важнейших разделов в информатике, для которых используется математика, и без знания которых нельзя составить ни одну программу или редактировать и изменять документы.
- Единицы информации, системы счисления, кодирование информации
- Алгоритмизация и программирование;
- Изучение логики.
В математической теории понятие «информация» связано с исключительно абстрактными объектами — случайными величинами, в то время как в современной теории информации это понятие рассматривается значительно шире — как свойство материальных объектов. Однако, без математического аппарата невозможно было бы представить современный компьютер, поскольку он основан на процессах хранения, обработки и передачи данных, которые, в свою очередь, основаны на математических принципах. К примеру, в большинстве современных компьютеров проблема сначала описывается в понятном им виде (при этом вся информация как правило представляется в двоичной форме — в виде единиц и нулей, хотя компьютер может быть реализован и на других основаниях, как целочисленных — например, троичный компьютер, так и нецелых), после чего действия по её обработке сводятся к применению простой алгебры логики. Быстрый электронный компьютер может быть применим для решения большинства математических задач, а также и большинства задач по обработке информации, которые могут быть сведены к математическим. Однако, было обнаружено, что компьютеры могут решить не любую математическую задачу. Впервые задачи, которые не могут быть решены при помощи компьютеров, были описаны английским математиком Аланом Тьюрингом. Таким образом, мы можем сделать вывод о том, что информатика как наука имеет под собой основу в виде математики. Поэтому, без математики в информационных технологиях никак нельзя обойтись (и здесь она играет доминантную роль). Да и как мы с вами уже выяснили, само определение компьютера - вычислитель, который основан на определённой целой или нецелой системы счисления, способный решать математические задачи и задачи по обработке информации.
Итак, первый урок - УРОК ЛИТЕРАТУРЫ
Как это не парадоксально, но с математикой в литературе, мы встречаемся практически повсеместно: математику используют герои многих литературных произведений, математика вдохновляет писателей на новые книги и идеи и так далее... В математике есть такое понятие, как закономерность, она окружает нас повсюду: день сменяется ночью, животные мигрируют на юг... Удивительно, однако, последовательности есть и в литературе. Например, стихотворный размер (это частная реализация стихотворного метра, его вариация). Существуют различные виды этого "размера". Есть односложные, двусложные и трехсложные размеры. в зависимости от того, на какой слог падает ударение, название размеров варьируется. Так, например, в стихотворении А.С. Пушкина:
Буря мглою небо кроет ∩́ __ / ∩́ __ /∩́ __ / ∩́_
Вихри снежные крутя ∩́ __ / ∩́ __ __ / __ ∩́
Ударение падает на каждый первый слог слов, состоящих из двух слогов (стоп), следовательно, это хорей - размер с ударением на первом слоге в стопе. Служение математике С.В. Ковалевская представляла себе неотрывным от служения литературе. В ней одновременно жили математик и поэт. Они одновременно родились, росли, учились, писали научные труды и стихи.
"Мне кажется, - говорила она, - что поэт должен видеть то, чего не видят другие, видеть глубже других. И это должен математик".
Для многих казалось странным, как она сочетает математику с поэзией. По этому поводу Ковалевская писала: "Многие, которым никогда не представлялось случая более глубоко узнать математику, считают её наукой сухой. В сущности же это наука, требующая наиболее фантазии, и один из первых математиков нашего времени говорит совершенно верно, что нельзя быть математиком, не будучи в то же время и поэтом в душе".
Если ты в жизни, хотя на мгновенье
Истину в сердце своём ощутил,
Если луч правды сквозь мрак и сомненье
Ярким сияньем твой путь озарил:
Чтобы в решеньи своём неизменном
Рок ни назначил тебе впереди -
Память об этом мгновеньи священном
Вечно храни, как святыню, в груди
Тучи сберутся громадой нестройной,
Небо покроется чёрною мглой,
С ясной решимостью, и с верной спокойной
Бурю ты встреть и померься с грозой.
Великий русский поэт М.Ю.Лермонтов был большим любителем математики и в своих вольных и невольных переездах из одного места службы в другое всегда возил с собою учебник математики.
Е щё один яркий пример использования математики в литературе - то, что многие произведения русских классиков содержат математические задачи. Как правило, авторы вставляют в свои произведения такие задачи чтобы украсить сюжет и сделать его интереснее. Вот например задача, встретившаяся мне в книге Жюль Верна «С Земли на Луну прямым путем за 97 часов 20 минут»
щё один яркий пример использования математики в литературе - то, что многие произведения русских классиков содержат математические задачи. Как правило, авторы вставляют в свои произведения такие задачи чтобы украсить сюжет и сделать его интереснее. Вот например задача, встретившаяся мне в книге Жюль Верна «С Земли на Луну прямым путем за 97 часов 20 минут»
«
Апогея и перигея Луны (рис. 1)
Луна описывает вокруг Земли не круг, а эллипс, в одном из фокусов которого находится наша планета; вследствие этого Луна в разное время находится в различных расстояниях от Земли; наибольшее расстояние называется апогеем, а наименьшее - перигеем. Как известно, разность между наибольшим и наименьшим расстоянием довольно велика, так что ею нельзя пренебрегать. В самом деле, в своем апогее Луна отстоит от Земли на 247552 мили, а в перигее ─ всего на 218657 миль; разница между двумя расстояниями достигает 28895 миль...»
Если мы посмотрим на расстояние, отделяющее Землю от ее спутника, то увидим, что оно различно. Правильно ли Жюль Верн сосчитал разницу между апогеем и перигеем (рис. 1) Луны?
Решение �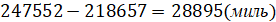 �
�
Проверяя данную задачу, мы получаем, что она верна, но, надо сказать что так бывает далеко не всегда..
Пример №2 Сказка "Конёк горбунок"

Задача
«Прекрасивых двух коней золотогривых
Да игрушечку-конька
Ростом только в три вершка,
На спине с двумя горбами
Да с аршинными ушами…»
Если мы попробуем перевести все старые меры длины в современные, то получится следующее:
Решение
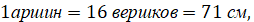
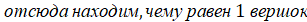
�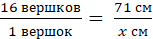 �, следовательно
�, следовательно
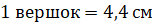
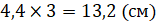
Получается, что конек-горбунок был ростом 13,2 см, а его уши были 71 см! Только представьте, уши конька-горбунка в 5 раз больше его роста! Имея аршинные уши, он не смог бы, не то чтобы летать, но и передвигаться. Их масса перевешивала бы самого конька-горбунка! Это задача неверна.
Можно ещё достаточно долго рассказывать о том, как математика может проявляться в литературных произведениях, но мне достаточно сложно не удержаться чтобы не упомянуть о самом, вероятно, известном писателе - Льюисе Кэрролле и о том, что он был превосходным математиком! Мало кто знает, но он автор таких замечательных книг как «Алгебраический разбор Пятой книги Эвклида», «Эвклид и его современные соперники» и многих других книг, в том числе, и знаменитой «Алиса в зазеркалье».
А теперь посмотрим как вы сочетаете в себе знания математики и литературы.
ПРАВИЛА: Время на обсуждение - 20 секунд. Готовность - поднятая рука.
ВОПРОСЫ ЛИТЕРАТУРНЫЕ:
1. Назовите имя известного поэта, математика, автора этих слов: "Яд, мудрецом тебе предложенный прими, Из рук же дурака не принимай бальзама!" (Омар Хайям)
2. Какой русский писатель окончил физико-математический факультет? (А.С. Грибоедов)
3. В сказке "Конек-горбунок" мы встречаем следующие слова: "Приезжаю - тьма народу! Ну ни выходу, ни входу!". Сколько было народа? (10 000)
4. Название какой кривой является в то же время литературным термином? (гипербола)
5. Кто из великих русских писателей составлял задачи по арифметике? (Л.Н. Толстой)
6. "В математике есть своя красота, как в поэзии". Кто произнес эти слова, даже не любя математику? (А.С. Пушкин)
ПЕРЕМЕНА - жюри подводит итоги, вопрос болельщикам (приложение)
Ведущий: Произведение одного среднеазиатского астронома и математика (787-850) называлось "Китаб мухтасар аль джебр ва-л-мукабала". Переводчик перевел все слова, слово "аль джебр" просто записал латинскими буквами. У него получилось слово - алгебра. Многие понятия и математические термины имеют иностранное происхождение. Посмотрим, как вы знаете иностранные языки.
УРОК ИНОСТРАННОГО ЯЗЫКА - (20 секунд на размышление)
1. Переведите на русский язык греческие слова - моно, ди, поли и латинские - уни, би, мульти (один, два, много)
2. Какая цифра в переводе с латинского означает " никакая"? (0)
3. Скажите по-гречески окружность, если для нас это часть страны, области, города, отдаленная от центра. (периферия)
4. У греков это натянутая тетива, а у нас? (гипотенуза)
5. Какая математическая единица измерения в переводе с латинского обозначает "ступень, шаг, степень"? (градус)
6. Какой геометрический термин образовался от латинского слова "отвесный"? (перпендикуляр)
ПЕРЕМЕНА - жюри подводит итоги, вопрос болельщикам (приложение)
УРОК МУЗЫКИ
Ведущий: Как вы думаете, математика имеет отношение к музыке?
На первых же уроках сольфеджио – так называются уроки музыкальной грамоты – ученики музыкальных школ сразу же сталкиваются с математикой. В музыке все считать надо. Как и в математике. 7 нот, 5 линеек нотного стана, интервалы. А ноты-то все разные. Одни коротенькие совсем, другие длинные. Так в 5-6 лет ребята, которые занимаются музыкой, узнают, что ноты или что-нибудь другое может делиться. А ведь деление школьники начинают изучать только в 8-9 лет, в конце второго класса.
Интересно, что у истоков музыкальной грамотности стоял великий математик Пифагор. Он относил к математике арифметику, геометрию, астрономию и музыку. Именно Пифагор ввел понятие гамма, которое окрестили - пифагоров строй.
И не случайно! Чтобы записать слова – мы используем буквы, числа – цифры, а музыку – ноты. При записи мелодии, звуки имеют свою длину (длительность). Здесь и происходит сопоставление целого числа и целой длительности, дробного числа и длительности коротких нот, записываемых при помощи дроби. Не зная математических понятий, не умея различать дроби, не умея сравнивать их, невозможно было бы сыграть музыкальный фрагмент. Именно здесь мы сталкиваемся с математической операцией сравнения. В музыке, как и в математике, тоже есть понятие параллельности. Параллельные тональности, а ещё линии нотного стана всегда параллельны, то есть никогда не пересекаются. Кроме вышеупомянутых понятий, с понятием последовательность в математике мы встречаемся крайне часто. Обычно цель при встрече с ними – отгадать следующее число или символ. Все музыкальные произведения тоже записываются нотами в определенной музыкальной последовательности. Исходя из всего выше перечисленного: в музыке крайне важно знать математику, а потому, последняя играет главенствующую роль при освоении музыки.
Вопросы музыкальные (20 секунд на размышление)
1. Без чего не могут обойтись охотники, барабанщики и математики? (Без дроби).
2. Люди какой профессии постоянно смотрят на 5 параллельных линий? (музыканты или дирижеры)
3. А сейчас я вас попрошу называть песни, в которых есть числительные или математические понятия по очереди побеждает команда которая назовет песня последней.
ПЕРЕМЕНА - жюри подводит итоги, вопрос болельщикам (приложение)
Ведущий:
В. Гюго заметил, что разум человеческий владеет 3 ключами, позволяющими людям знать, думать и мечтать. Ключи эти следующие - буква, нота и цифра.
Давайте, определим, как вы можете сочетать буквы и цифры.
УРОК РУССКОГО ЯЗЫКА - тема урока " Числительные"
1. Заполнить таблицы- 15 минут

| Задание | Ответы |
| Все за одного, . . . за всех. | один |
| . . . раз примерь, . . . раз отрежь. | семь, один |
| Не имей . . . рублей, а имей . . . друзей. | сто, сто |
| Ум хорошо, а . . . лучше. | два |
| За . . . зайцами погонишься, ни . . . не поймаешь. | двумя, одного |
| У . . . нянек дитя без глаза. | семи |
| Обещанного . . . года ждут. | три |
| . . . в поле не воин. | один |
| Скупой платит . . ., а лентяй . . . работает. | дважды |
| . . . сапога – пара. | два |
| Знать, как свои . . . пальцев. | пять |
| . . . . . . не ждут. | семеро одного |
Анаграммы
| Задание | Ответы |
| ТИМАКАМАТЕ | Математика |
| МАОТЕРЕ | Теорема |
| ЖЕСЛОНИЕ | Сложение |
| РИФГАМЛО | Логарифм |
| ГЕБРААЛ | Алгебра |
| НЕУРАВНИЕ | Уравнение |
| ЩАПДЬЛО | Площадь |
| МЕТГРИЯЕО | Геометрия |
| ЖЕУМНОНИЕ | Умножение |
| ЦИЯПЕТРА | Трапеция |
| ВООНАЯБРАЗПЕР | Первообразная |
| ГОЛЬТРЕУНИК | Треугольник |
| НДРЛИЦИ | Цилиндр |
| НАЯИЗВОДПРО | Производная |
| ЧИТАВЫНИЕ | Вычитание |
| ИКРАФГ | График |
| МЕТРИТНОРИЯГО | Тригонометрия |
| АДКВРАТ | Квадрат |
| НИКМГОРАННОГ | Многогранник |
| НИЕЛЕДЕ | Деление |
| ЗМАПРИ | Призма |
| ТНИКГОЛЬРЕУ | Треугольник |
| РАЛИНТЕГ | Интеграл |
| СИОМААК | Аксиома |
Пока команды работают болельщики должны будут по очереди говорить пословицы и поговорки, в которых используются названия чисел. Эстафета заканчивается, если болельщики замолкают.
ПЕРЕМЕНА - жюри подводит итоги, вопрос болельщикам
Вопросы пока жюри подводят итоги (20 секунд на размышление)
1. Что есть у каждого слова, растения и уравнения? (Корень).
2. Какие прилагательные русского языка в математике становятся именами существительными? (прямая, кривая, ломаная, касательная, секущая, наклонная)
3. Какая цифра в русском языке является глаголом повелительного наклонения единственного числа? (три!)
4. С буквой "и" - это глагол русского языка настоящего времени, являющийся синонимом глагола "движет". С буквой "е" - это существительное, обозначающее сторону треугольника. ( катит-катет)
ВЕДУЩИЙ:
Арифметика! Даже в каменный век
Обращался к тебе человек.
Без тебя невозможно предметы считать,
Невозможно построить мосты
Там, где сложное, новое надо создать,
Лучшим другом становишься ты.
Если раньше тебе приходилось одной
Много трудных вопросов решать,
То теперь на просторах планеты большой
Ты у нас многодетная мать.
Геометрия, алгебра - дети твои,
С ними в жизнь претворяем мечты,
Но запомни: огромным успехом своим
Человеку обязана ты.
УРОК ИСТОРИИ (20 секунд на размышление)
Математика и история - две неразрывные области знания. История обогащает математику гуманитарным и эстетическим содержанием, развивает образное мышление учеников. Математика, развивающая логическое и системное мышление, занимает достойное место в истории, помогая лучше ее понять. Одним из основных способов исследований в области истории и математики является Клиометрика (англ. Cliometrics) —междисциплинарное направление, исследований на стыке истории, экономики и математики. Кстати, к сведению, в Греции Клио – муза истории в древнегреческой мифологии, следовательно, клиометрика и клиодинамика - это, соответственно, историометрика и историческая динамика.
Первые опыты применения средств математики для обработки исторических материалов относятся к 60-м гг. XVII в. Английские «политические арифметики» Д. Граунт и В. Петги попытались проанализировать данные демографии. Долгие годы данные о народонаселении были единственной точкой соприкосновения математических методов и исторических материалов. Дальнейший перелом произошел лишь в 60-х гг. в Европе и в 70-х гг. XIX в. в России. Первыми учеными, высказавшимися за целесообразность использования математико-статистических методов были в Европе - Т. Бокль, в России - И.В. Лучицкий. С этих пор в истории применяются простейшие статистические методы (группировка, расчет показателей вариации и др.). Использование математических методов осуществлялось в большей степени в тех сферах исторического познания, где был накоплен большой опыт источниковедческого анализа традиционными средствами. Именно применение математических методов позволило вывести на новый уровень изучение данных проблем. В настоящее время складываются области исторического исследования, которые строятся на такого рода обобщении и предусматривают применение широкого спектра новейших методик.
Чтобы понять, возможна ли математическая история или это просто набор достаточно произвольных моделей, нам нужно знать, сможем ли мы проверять наши гипотезы с помощью данных. И выясняется, что да, что в истории существует гигантское количество данных, с помощью которых мы можем все наши теории проверять.
К примеру, политическая нестабильность. Тут нам очень помогают клады монет. Дело в том, что монеты датируются очень хорошо, на многих монетах отчеканен год, когда они были выпущены. Мы можем достаточно точно определить, когда клад был зарыт. Для многих регионов существуем перепись кладов, которые были найдены. Например, в Московской области сотни кладов, они переписаны и нам известны более-менее промежутки, когда эти клады были зарыты. Так вот выяснилось, что существует очень хорошая взаимосвязь между периодами нестабильности и количеством кладов за десятилетие, которые были зарыты и потом не востребованы. Понятно, почему. Во-первых, люди зарывают клады в период, гражданской войны, осложнения внутреннего положения или вторжения чужой армии в государство. Во время стабилизации обстановки клады могли отрыть, но если хозяева погибли или, скажем, были вынуждены эмигрировать куда-то, то эти клады оставались в земле. Именно эти наслоения по времени дают нам динамическую картину политической нестабильности. Ещё одним, наиболее ярким примером использования математики в истории это хронология, даты и события. Все события происходят по определенным закономерностям. Кстати говоря, сама идея цикличности противостояла идее прогрессивного поступательного развития человеческой культуры в XIX — начале XX в., она представлена в движении культурно-исторических типов у Н. Данилевского, развитии жизни «культурных организмов» в концепции О. Шпенглера, круговороте «локальных цивилизаций» А.Тойнби, теории «этногенеза» Л. Гумилёва. а символом этой теории послужила спираль.
Интересно, что нынешний календарь составлен неправильно, а все потому, что древние монахи считали на абаке и попросту не знали что такое ноль. Вот почему сейчас ученые говорят о том, что вследствие незнания такого простого числа, и несовершенных расчетов с большими погрешностями, мы в настоящее время говорим о том, что 2000 год это неформально 21 век а официально век 20. Посудите сами, на первый взгляд, такой стиль нумерации (без нуля) не кажется особенно плохим, однако он гарантировал неприятности. Посмотрите на годы новой эры как на положительные числа, а на годы до новой эры как на отрицательные. Эта датировка выглядела следующим образом: -3, -2, -1, 1, 2, 3... Ноль, законное место которого между -1 и 1 отсутствовал. Представьте, что ребенок родился 1 января 4 года до нашей эры. В третьем году до н.э. ему исполнился год до н.э.; во втором 2 года до н.э.; в первом году до нашей эры 3 года; во втором году н.э. - 5 лет. Очевидно? В наше время есть версия что Иисус родился в 4 году до н.э. а, следовательно, для того чтобы произвести расчет, в нашем случае необходимо было из 2 вычесть минус четыре( 2-(-4)), однако, полученный результат был бы равен 6, что в корне неверно, потому что для подсчета не использовался ноль. А неправильное летоисчисление изменяет всю хронологию, что влечет за собой, зачастую, печальные последствия. Сама по себе хронология - наука, изучающая счет времени. Календарь - яркие пример геометрической модели деления отрезков (в данном случае по времени). Сейчас мы живем по Григорианскому календарю, поэтому, чтобы установить точную дату в историческом источнике, которая соответствовала Юлианскому календарю или календарю "от сотворения мира", историки используют специальную формулу. Сейчас возникает идея о пересмотре календарной системы, но, наверное, историкам следует отказаться от неё, т.к. придется переделывать все исторические даты. Многие математические структуры нашли свое применение в истории, такие, как например, строение герба, в которой каждая часть имеет свое название и смысл. Поэтому, можно смело судить о том, что математика играет действительно важную роль при изучении истории.
1. Петр Первый хорошо знал адицию, субстракцию, мультипликацию и дивизию. В его времена эти действия знали далеко не все, и Петр настойчиво заставлял изучать это своих сподвижников. Сейчас это знает каждый школьник. Как он это называет? ( + - * /)
2. Что на Руси раньше называли "ломаными числами" (дроби)?
3. Сколько подвигов совершил Геракл? (12)
4. О какой науке Цицерон сказал: "Греки изучали её, чтобы познать мир, а римляне - для того, чтобы измерять земельные участки" (геометрия)
5. Летописец сообщает, что строительство Успенского Собора в Кремле велось "в кружало и а правило". К помощи каких инструментов прибегли мастера? (циркуль и линейка)
6. Почему в Египте строители пирамид использовали веревку с 12 узелками? (образ. прямоугольный треугольник со сторонами 3, 4, 5)
ПЕРЕМЕНА - жюри подводит итоги, вопрос болельщикам (приложение)
Ведущий:
Настало время урока математики для ваших капитанов команд. Капитаны будут сегодня сдавать экзамен. Каждому предлагаю тест из 12 блиц-вопросов, на которые вы отвечаете на специальном бланке.
1) Как назывался главный труд древнегреческого математика Евклида?
А) "Основы" Б) "Начала" В) "Старты" Г) " Истоки"
2) Какой раздел математики греки называли " искусством чисел"?
А) Арифметика Б) Алгебра В) Математический анализ Г) теория чисел
3)Какие бывают современные фотоаппараты?
А)Цифровые Б) Числовые В) Формульные Г) Логарифмические?
4) Какие числа употребляются при счете?
А) Природные Б) Естественные В) Натуральные Г) Искусственные
5)Как называют незаинтересованного в конфликте между сторонами, беспристрастного?
А) Третья сторона Б) пятая сторона, В) Седьмая сторона Г) десятая сторона
6) Как называют верхний угол футбольных ворот?
А) Десятка Б) девятка В) Шестерка Г) Пятерка
7)Как в древнерусском счете называлось число 100 тысяч ?
А) Легион Б) Когорта В) Полк г) Орда
8)Какое из этих выражений является синонимом слова "мало"
А)Куры не клюют Б) Пруд пруди В)Кот наплакал Г) Ворона накаркала
9)Под каким псевдонимом выступает на арене главный герой оперетты Кальмана "Принцесса цирка"?
А) Сэр Игрек Б) Мистер ИКС В) Лорд Зет Г)Синьор Пи
10)Какими бывают математические неравенства?
А) Неточными Б) нестрогими В) Невежливыми г) Невоспитанными
11) Закончите название книги Дж. Толкиена " Властелин … "
А) Пирамид Б) Шаров В) Колец Г) Икосаэдров
12) Закончите русскую пословицу" Всякому мила своя …"
А) высота Б)сторона В) медиана Г) биссектриса
Пока капитаны работают команды также не будут отдыхать предлагаю вам посчитать треугольники и квадраты
Конкурс - “ Посчитай-ка ”
Сколько треугольников в данном прямоугольнике?
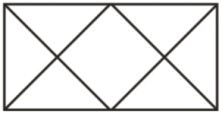 12
12
Сколько треугольников на рисунке?
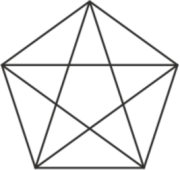 35
35
Сколько квадратов в данном прямоугольнике?
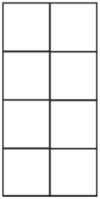 11
11
Сколько квадратов в данном прямоугольнике?
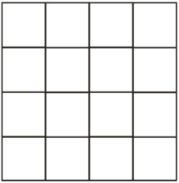 30
30
Для болельщиков ребусы:
| Задание | Ответы |
| У 3‘ О | утро |
| С В И 1 0 0 К | свисток |
| 4 0 А | сорока |
| П И 1 0 0 Л Е Т | пистолет |
| С 3 Ж | стриж |
| Р О 1 0 0 К | росток |
| 7’ Е Н А | семена |
| 1 0 0 Л Б | столб |
| П А ‘3 Ж | Париж |
| А И 1 0 0’ | аист |
| З А 1 К А | заколка |
| Л И 1 0 0 К | листок |
| 1 У М | разум |
| 7 Я | семья |
| Ш 3 Х | штрих |
| В И 3 Н А | витрина |
| П О 2 Л | подвал |
| С 3 Ж К А | стрижка |
| Ф 1 А | Фраза |
| Т Е 1 0 0 | Тесто |
| Ш 1 А | Школа |
| И 1 0 0 Р И Я | История |
| 2 Д | Парад |
Сдавайте свои ответы на стол жюри, пока они подводят итоги, я хотела бы закончит нашу встречу словами:
Запомни, что Гаусс всем сказал
Наука математика - царица всех наук.
Не зря, поэтому он завещал -
Творить в огне трудов и мук.
Безмерна роль её в открытии законов,
В создании машин, воздушных кораблей
Пожалуй, трудно нам пришлось бы без Ньютонов
Каких дала история до наших дней
Пусть ты не станешь Пифагором,
Каким хотел бы может быть
Но будешь ты рабочим, иль ученым
И будешь честно Родине служить.
Жюри объявляет результаты, награждает команду - победительницу "5" по математике, называет отличившихся болельщиков, награждая - "5" и самых активных членов команд, награждая их "4"
Используемая литература:
Агеева И.Д. Занимательные материалы по информатике и математике. – М.: Творческий центр "Сфера", 2006.
Депман И., Виленкин Н. За страницами учебника математики. – М.: "Просвещение", 1989.
Газеты "Математика" и "Информатика". Приложения к газете "1 сентября".
ПРИЛОЖЕНИЕ 1
ВОПРОСЫ ДЛЯ БОЛЕЛЬЩИКОВ:
В 7-8 веках нашей эры один ирландский монах изложил способ счета от 0 до 1 млн, которым до сих пор пользуются биржевые маклеры на чикагской хлебной бирже. Чем они пользуются? (пальцами)
У южноамериканского племени таманаки число 6 -это один палец другой руки, 11- один палец ноги, А как по-таманакски будет 21? (один палец руки другого человека)
Каков вклад английского поэта Байрона в историю вычислений? (его дочь - Ада Лавлейс -первый программист- помощница Ч. Беббиджа)
В каком м/ф главному герою помогло знание техники для борьбы со злыми силами? ("Ивашка из Дворца пионеров")
Петр Первый издал указ: " Учить всех дворянских детей "цифири и геометрии", а тем, кто не усваивал этих премудростей он запрещал … . (жениться)
Леонардо да Винчи записывал в блокнот числа после встречи с людьми, которые представляли для него художественный интерес. Что означали эти числа? (это был способ запомнить их лица)
Как назывался прибор, используемый для арифметических вычислений в Др. Греции, Риме? (абак)
Как называлось устройство, которой имело в своем составе контору, фабрику и склад? (разностная вычислительная машина Ч. Беббиджа)
Каков девиз фирмы IBM и каждого успешного ученика? ("Думай!")
У известного русского поэта есть такие строки " Мы почитаем всех 0, а единицами - себя". Кто, таким образом, воспевал числа двоичной системы? (А.С. Пушкин)
Что больше - сумма арабских цифр или их произведение? (сумма)
Какая дробь находится между каникулами? (1/4-четверть)
Какая страна является родиной арабских цифр? ( Индия)
Сколько десятков получится, если умножить 3 десятка на 3 десятка? ( 90 десятков)
Какой угол образует с экватором меридиан ? (прямой)
Назовите любимую фразу Евклида, которую вы часто произносите на уроках геометрии. (что и требовалось доказать)
Где находится ноль в нашем городе? (главпочтамт)
ПРИЛОЖЕНИЕ 2
Таблица результатов
Правильный ответ -1 балл
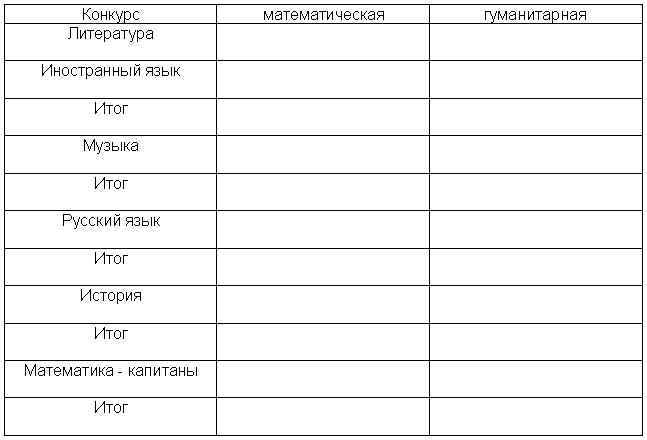
ПРИЛОЖЕНИЕ 3
“ Найти слова ”
| Д | Е | Е | Р | Е | Т | Р | Е | О |
| У | Л | П | И | М | Я | Ч | А | М |
| Р | И | М | О | Е | С | Ы | Т | Е |
| А | В | Н | З | Р | А | З | Н | А |
| И | Н | Е | А | Д | А | Ч | О | Ш |
| Е | Р | А | Т | М | А | А | С | Ь |
| К | Д | И | К | А | Т | Ь | Т | Н |
| В | А | Т | А | М | Е | У | М | Е |
Найдите слова: математика, квадрат, периметр, уравнение, делимое, тысяча, задача, разность, уменьшаемое.
ПРИЛОЖЕНИЕ 4
Конкурс капитанов
1) Как назывался главный труд древнегреческого математика Евклида?
А) "Основы" Б) "Начала" В) "Старты" Г) " Истоки"
2) Какой раздел математики греки называли " искусством чисел"?
А) Арифметика Б) Алгебра В) Математический анализ Г) теория чисел
3)Какие бывают современные фотоаппараты?
А)Цифровые Б) Числовые В) Формульные Г) Логарифмические?
4) Какие числа употребляются при счете?
А) Природные Б) Естественные В) Натуральные Г) Искусственные
5) Как называют незаинтересованного в конфликте между сторонами, беспристрастного?
А) Третья сторона Б) пятая сторона, В) Седьмая сторона Г) десятая сторона
6) Как называют верхний угол футбольных ворот?
А) Десятка Б) девятка В) Шестерка Г) Пятерка
7)Как в древнерусском счете называлось число 100 тысяч ?
А) Легион Б) Когорта В) Полк г) Орда
8)Какое из этих выражений является синонимом слова "мало"
А)Куры не клюют Б) Пруд пруди В)Кот наплакал Г) Ворона накаркала
9)Под каким псевдонимом выступает на арене главный герой оперетты Кальмана "Принцесса цирка"?
А) Сэр Игрек Б) Мистер ИКС В) Лорд Зет Г)Синьор Пи
10)Какими бывают математические неравенства?
А) Неточными Б) нестрогими В) Невежливыми г) Невоспитанными
11) Закончите название книги Дж. Толкиена " Властелин … "
А) Пирамид Б) Шаров В) Колец Г) Икосаэдров
12) Закончите русскую пословицу" Всякому мила своя …"
А) высота Б)сторона В) медиана Г) биссектриса
1. Листы для капитанского конкурса
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.







 щё один яркий пример использования математики в литературе - то, что многие произведения русских классиков содержат математические задачи. Как правило, авторы вставляют в свои произведения такие задачи чтобы украсить сюжет и сделать его интереснее. Вот например задача, встретившаяся мне в книге Жюль Верна «С Земли на Луну прямым путем за 97 часов 20 минут»
щё один яркий пример использования математики в литературе - то, что многие произведения русских классиков содержат математические задачи. Как правило, авторы вставляют в свои произведения такие задачи чтобы украсить сюжет и сделать его интереснее. Вот например задача, встретившаяся мне в книге Жюль Верна «С Земли на Луну прямым путем за 97 часов 20 минут»

 12
12 35
35 11
11 30
30










