Методика математического моделирования на компьютере

Типы информационных моделей

Табличные – объекты и их свойства представлены в виде списка, а их значения размещаются в ячейках прямоугольной формы. Перечень однотипных объектов размещен в первом столбце (или строке), а значения их свойств размещаются в следующих столбцах (или строках)

Иерархические – объекты распределены по уровням. Каждый элемент высокого уровня состоит из элементов нижнего уровня, а элемент нижнего уровня может входить в состав только одного элемента более высокого уровня

Сетевые – применяют для отражения систем, в которых связи между элементами имеют сложную структуру

По степени формализации информационные модели бывают образно-знаковые и знаковые. Например:

Образно-знаковые модели :

Геометрические (рисунок, пиктограмма, чертеж, карта, план, объемное изображение)

Структурные (таблица, граф, схема, диаграмма)

Словесные (описание естественными языками)

Алгоритмические (нумерованный список, пошаговое перечисление, блок-схема)

Знаковые модели

1. Математические – представлены математическими формулами, отображающими связь параметров.

2. Специальные – представлены на специальных языках (ноты, химические формулы)

3. Алгоритмические – программы

Предметом изучения информатики являются методы и технологии информационного моделирования с помощью компьютера – компьютерное моделирование.

Компьютерной моделью называют модель, построенную для исполнителя, ориентированного на вычислительное устройство. Это не особый вид модели, а способ изучения известных моделей с помощью компьютера.

Компьютерная математическая модель – это программа, реализующая расчёты состояния моделируемой системы по её математической модели.

Математическое моделирование – это связь между объектами в виде математических соотношений. При этом информационные объекты представляются в виде математических объектов.

Пример. Модель равноускоренного движения: St = So + VoT + aT^2/2

В основу классификации математических моделей можно положить различные принципы. Можно классифицировать модели по отраслям наук (математические модели в физике, биологии, социологии и т.д.). Можно классифицировать по применяемому математическому аппарату (модели, основанные на применении обыкновенных дифференциальных уравнений, дифференциальных уравнений в частных производных, стохастических методов, дискретных алгебраических преобразований и т.д.). Наконец, если исходить из общих задач моделирования в разных науках безотносительно к математическому аппарату, наиболее естественна такая классификация:

• дескриптивные  (описательные)  модели;

• оптимизационные модели;

• многокритериальные модели;

• игровые модели.

Дескриптивные (описательные) модели. Например, моделирование движения кометы, вторгшейся в Солнечную систему, производится с целью предсказания траектории ее полета, расстояния, на котором она пройдет от Земли, и т.д. В этом случае цели моделирования носят описательный характер, поскольку нет никаких возможностей повлиять на движение кометы, что-то в нем изменить.

Оптимизационные модели используются для описания процессов, на которые можно воздействовать, пытаясь добиться достижения заданной цели. В этом случае в модель входит один или несколько параметров, доступных влиянию. Например, меняя тепловой режим в зернохранилище, можно задаться целью подобрать такой режим, чтобы достичь максимальной сохранности зерна, т.е. оптимизировать процесс хранения.

Многокритериальные модели. Нередко приходится оптимизировать процесс по нескольким параметрам одновременно, причем цели могут быть весьма противоречивыми. Например, зная цены на продукты и потребность человека в пище, нужно организовать питание больших групп людей (в армии, детском летнем лагере и др.) физиологически правильно и, одновременно с этим, как можно дешевле. Ясно, что эти цели совсем не совпадают, т.е. при моделировании будет использоваться несколько критериев, между которыми нужно искать баланс.

Игровые модели могут иметь отношение не только к компьютерным играм, но и к весьма серьезным вещам. Например, полководец перед сражением при наличии неполной информации о противостоящей армии должен разработать план: в каком порядке вводить в бой те или иные части и т.д., учитывая и возможную реакцию противника. Есть специальный раздел современной математики — теория игр, — изучающий методы принятия решений в условиях неполной информации.

Этапы компьютерного математического моделирования 

Первый этап —определение целей моделирования. Эти цели могут быть различными:

1. модель нужна для того, чтобы понять, как устроен конкретный объект, какова его структура, основные свойства, законы развития и взаимодействия
   с окружающим миром (понимание);

2. модель нужна для того, чтобы научиться управлять объектом (или процессом)  и определить наилучшие способы управления при заданных целях и критериях (управление);

3. модель нужна для того, чтобы прогнозировать прямые и косвенные последствия реализации заданных способов и форм воздействия на объект (прогнозирование).

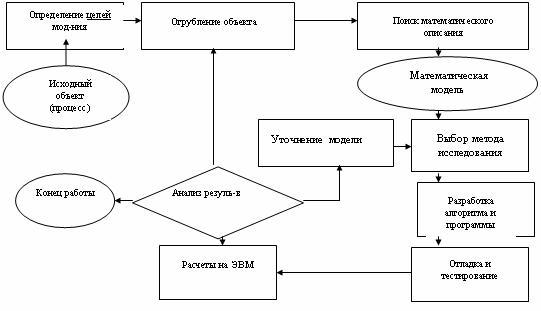
Второй этап: определение входных и выходных параметров модели; разделение входных параметров по степени важности влияния их изменений на выходные. Такой процесс называется ранжированием, или разделением по рангам.

Третий этап: построение математической модели. На этом этапе происходит переход от абстрактной формулировки модели к формулировке, имеющей конкретное математическое представление. Математическая модель — это уравнения, системы уравнений, системы неравенств, дифференциальные уравнения или системы таких уравнений и пр.

Четвертый этап: выбор метода исследования математической модели. Чаще всего здесь используются численные методы, которые хорошо поддаются программированию. Как правило, для решения одной и той же задачи подходит несколько методов, различающихся точностью, устойчивостью и т.д. От верного выбора метода часто зависит успех всего процесса моделирования.

Пятый этап: разработка алгоритма, составление и отладка программы для ЭВМ — трудно формализуемый процесс. Из языков программирования многие профессионалы для математического моделирования предпочитают FORTRAN: как в силу традиций, так и в силу непревзойденной эффективности компиляторов (для расчетных работ) и наличия написанных на нем огромных, тщательно отлаженных и оптимизированных библиотек стандартных программ математических методов. В ходу и такие языки, как PASCAL, BASIC, С, — в зависимости от характера задачи и склонностей программиста.

Шестой этап: тестирование программы. Работа программы проверяется на тестовой задаче с заранее известным ответом. Это — лишь начало процедуры тестирования, которую трудно описать формально исчерпывающим образом. Обычно тестирование заканчивается тогда, когда пользователь по своим профессиональным признакам сочтет программу верной.

Седьмой этап: собственно, вычислительный эксперимент, в процессе которого выясняется, соответствует ли модель реальному объекту (процессу). Модель достаточно адекватна реальному процессу, если некоторые характеристики процесса, полученные на ЭВМ, совпадают с экспериментально полученными характеристиками с заданной степенью точности. В случае несоответствия модели реальному процессу возвращаемся к одному из предыдущих этапов.

 Компьютерная реализация моделей может быть осуществлена:

• с помощью табличного процессора ( MS Excel);

• путем создания программ на традиционных языках программирования  (Паскаль, Бейсик и др.), а также на их современных версиях;

• с помощью специальных пакетов прикладных программ для  решения  математических  задач (3D MAX и т.п.).

Основные этапы разработки и исследования моделей на компьютере

1. Построение описательной информационной модели

2. Формализация модели (формальный язык)

3. Преобразование в компьютерную модель:

• запись алгоритма на языке программирования

• использование одного из приложений ( электронных таблиц, СУБД)

1. Проведение компьютерного эксперимента (запуск программы, сортировка или поиск данных, построение графиков и диаграмм)

2. Анализ полученных результатов и корректировка исследуемой модели.

Пример математического моделирования с помощью программы

MS Excel

Задача: Из трех продуктов 1,2,3 составляют смесь. В состав смеси должно входить не менее 6 единиц химического вещества А, 8 единиц – вещества В и не менее 12 единиц вещества С. Структура химических веществ приведена в следующей таблице:

Таблица 1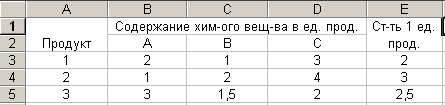

Составьте наиболее дешевую смесь.

Решение

1. Добавим 2 столбца количество и сумма. В столбец Количество поставим свое значение. Сумму найдем, умножив количество на стоимость 1 единицы продукта.

Таблица 2

1. Для нахождения поиска решения введем ограничения

Таблица 3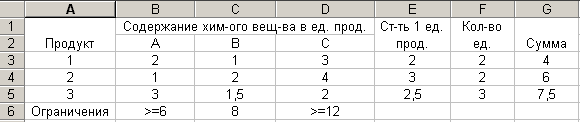

1. Введем строку Смесь и найдем состав

Таблица 4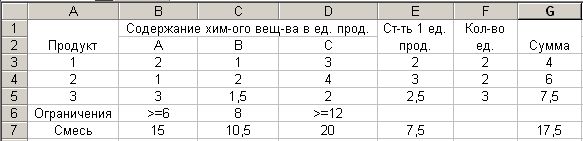

1. С помощью поиска решения найдем наиболее дешевую смесь

Таблица 5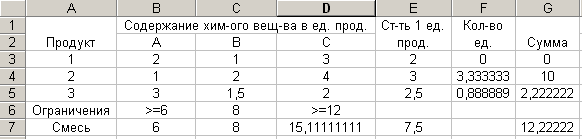

1. Таблица с формулами

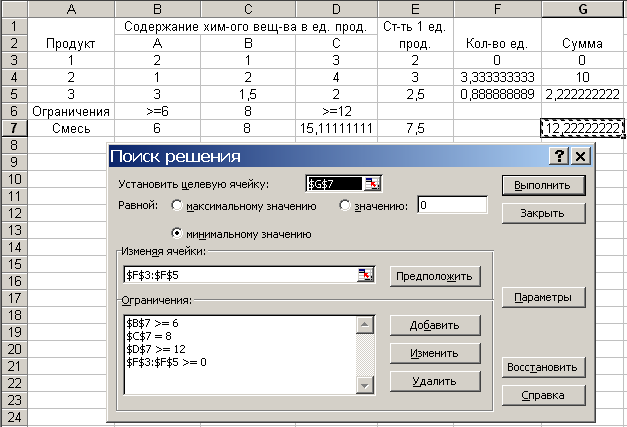1. Результаты поиска решения

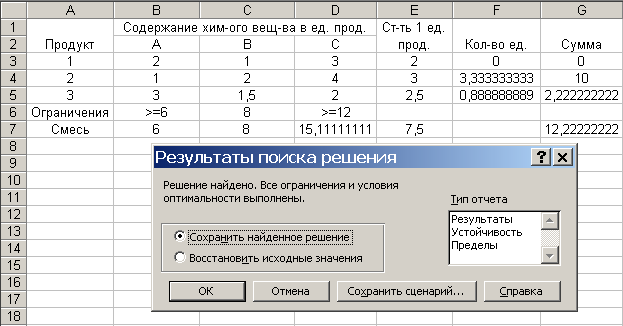
Составление математической модели для алгоритма оптимизации.

Введем обозначения

I – номер строки, продукт

J – номер столбца, химического вещества

R_ij – норма расхода одного продукта в смеси

X_j – содержание j-го химического вещества в продукте

P_i – стоимость 1 продукции

B_j – ограничения

Целевая функция

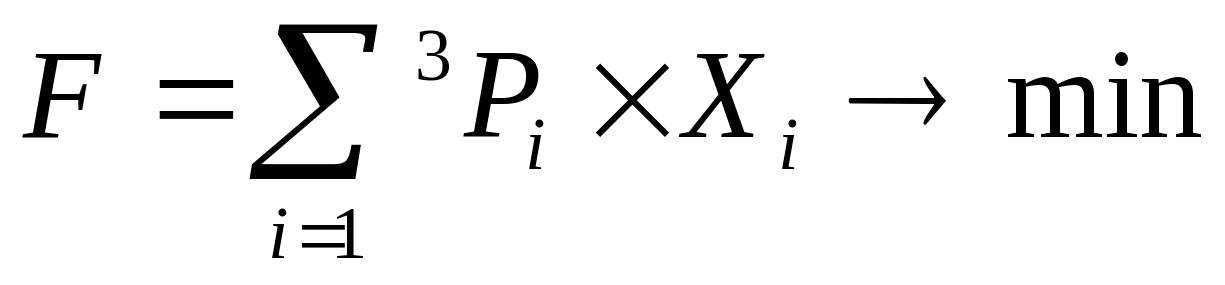
Общая формула для ограничений

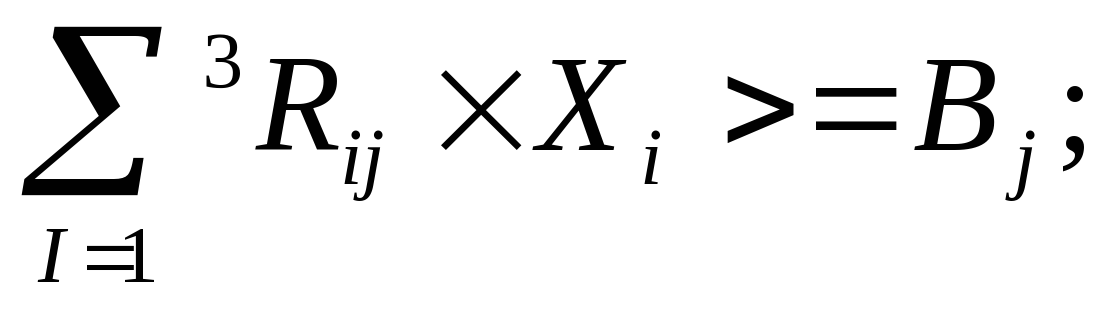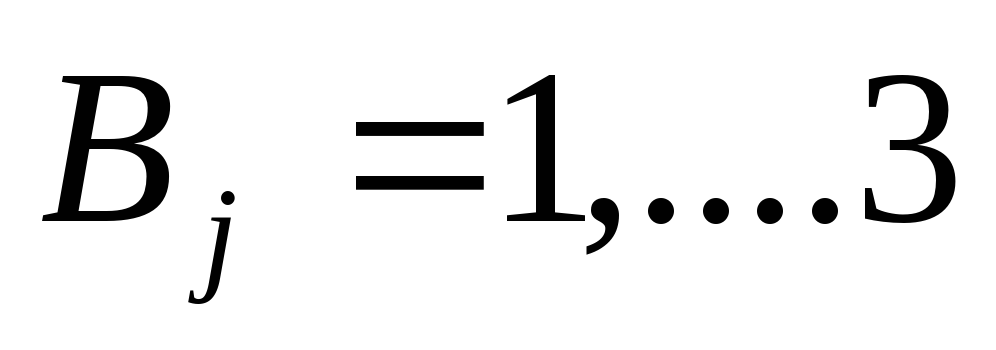
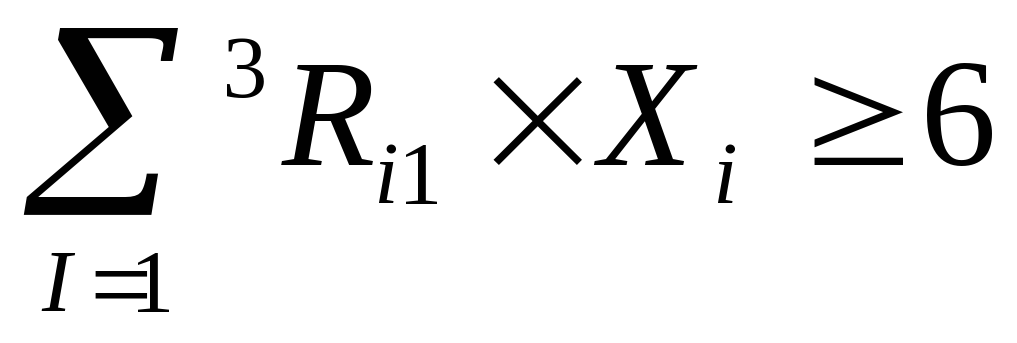
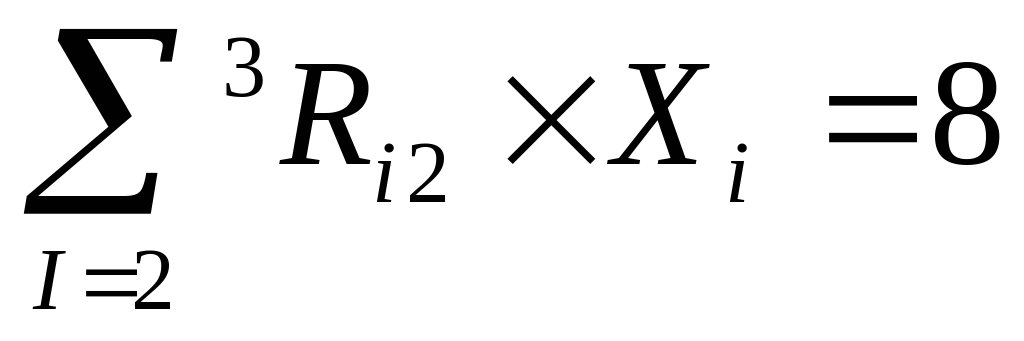
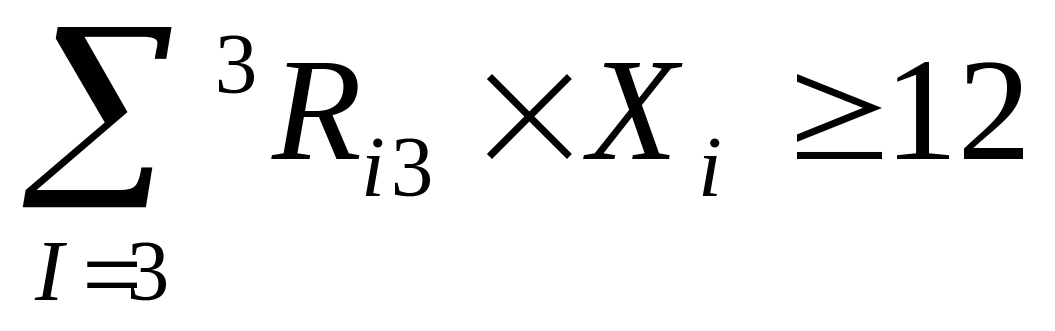
Практическая часть

Задание

1. Выполнить вычислительный эксперимент со свободным падением тела (таблица стр. 34-35, 11 класс, часть 2)

1. Рассчитать время падения шара в воде с точностью до 0,01 секунды (готовая программа на Паскале стр. 36, 11 класс, часть 2)

Контрольные вопросы

1. Что означает понятие модель в научном познании?

2. Какие типы моделей вам известны?

3. Дать определение информационной модели.

4. Что такое компьютерное моделирование?

5. Назовите основные этапы математического моделирования.

6. Назовите основные этапы решения задачи на ЭВМ