Урок № 2
Ознаки подільності на 10, на 5, на 2
Мета уроку: ознайомити учнів з ознаками подільності натуральних чисел на 10, 5, 2 та сформувати вміння застосовувати їх до розв’язання задач; розвивати здатність логічно обґрунтовувати математичні твердження, вміння працювати з підручником; виховувати самостійність.
Очікувані результати: учні повинні вміти наводити приклади парних і непарних чисел; чисел, що діляться націло на 5, 10, формулювати ознаки подільності на 10, 5, 2 та розв’язувати вправи, що передбачають використання ознак подільності на 2, 5 і 10.
Обладнання та наочність: підручник, презентація, відеоматеріал
Тип уроку: урок засвоєння нових знань.
 Словничок (глосарій):
Словничок (глосарій):
Непарна цифра – будь-яка з цифр 1, 3, 5, 7, 9.
Непарне число – натуральне число, десятковий запис якого закінчується непарною цифрою.
Подільність націло натурального числа a на натуральне число b – існування такого натурального числа c, що є правильною рівність a = b · c.
Ознака подільності на натуральне число – необхідна і достатня умова подільності націло деякого натурального числа на дане натуральне число.
Парна цифра – будь-яка з цифр 0, 2, 4, 6, 8.
Парне число – натуральне число, десятковий запис якого закінчується парною цифрою.
■ I. Перевірка додаткового завдання
Розв’язання
Дільники числа 6: 1; 2; 3; 6. 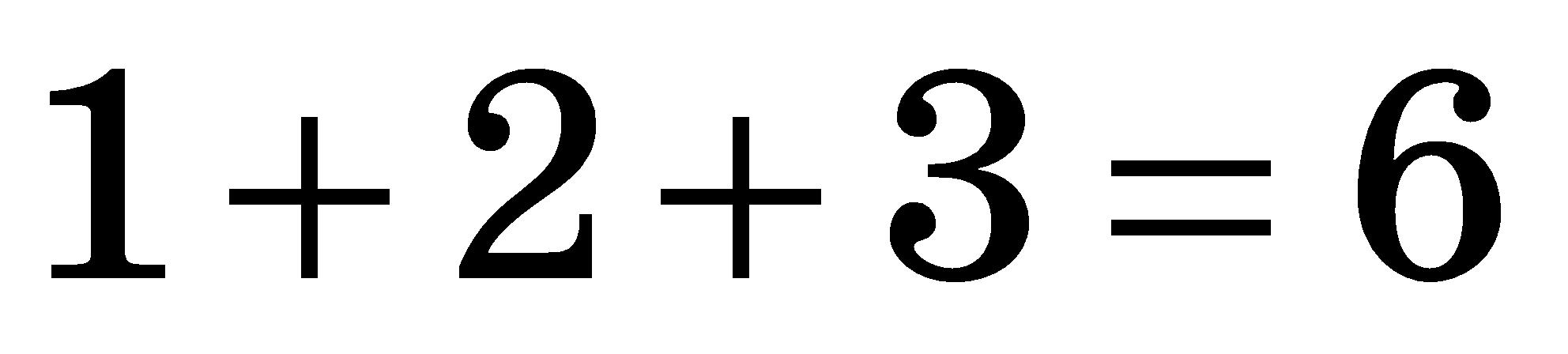 .
.
Дільники числа 28: 1; 2; 4; 7; 14; 28. 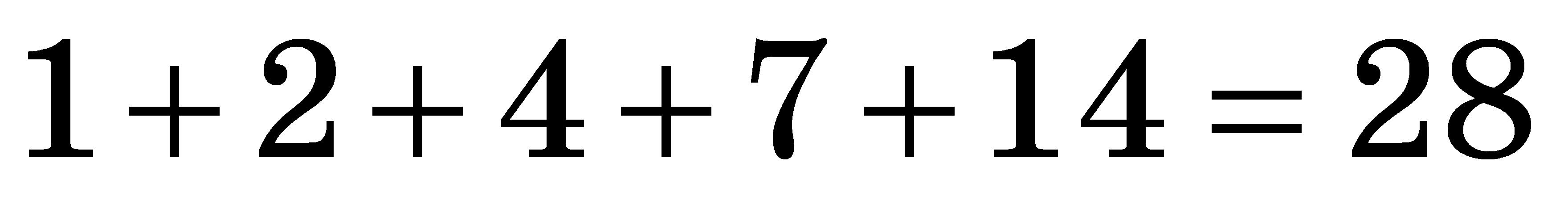 .
.
Дільники числа 496: 1; 2; 4; 8; 16; 31; 62; 124; 248; 496. 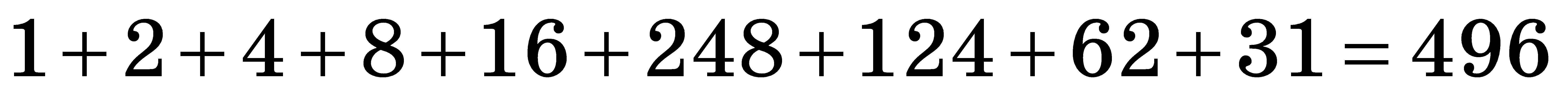 . Отже, всі дані числа — досконалі.
. Отже, всі дані числа — досконалі.
■ II. Актуалізація опорних знань
▪Опитування
Якщо натуральне число a ділиться без остачі на натуральне число b, то a є ..., b є ...
Чи правильним є твердження, що число 8 — дільник числа 72?
Чи правильним є твердження, що число 100 — кратне числа 10?
Яке число є дільником кожного натурального числа?
Яке число є найбільшим дільником числа 2 153 849?
Чи може продавець дати здачу 2 грн. 45 к. монетами по 25 к.?
Відповіді на питання
1. …кратним, а b є дільником. 2. Так. 3. Так. 4. 1. 5. 2 153 849. 6. Ні.
■ III. Формулювання завдань заняття; мотивація навчальної діяльності.
 Чи можна, не виконуючи ділення, а тільки за зовнішнім виглядом числа встановити, чи ділиться, наприклад, число 19348 на 2, число 917 595 на 5 або 10? На цьому занятті ми ознайомимося з правилами(ознаками), які підтвердять або спростують ваші припущення.
Чи можна, не виконуючи ділення, а тільки за зовнішнім виглядом числа встановити, чи ділиться, наприклад, число 19348 на 2, число 917 595 на 5 або 10? На цьому занятті ми ознайомимося з правилами(ознаками), які підтвердять або спростують ваші припущення.
▪ Мотивація навчальної діяльності
За скільки секунд можна визначити, які з чисел 2548; 243 789; 13 578 діляться на 2? Запишіть ряд чисел, кратних числу 5. З якого числа починається цей ряд? На скільки кожне наступне число в цьому ряді більше від попереднього?
■ IV. Засвоєння нових знань
План викладання нового матеріалу
1. Ознаки подільності на 10.
2. Ознаки подільності на 5.
3. Ознаки подільності на 2.
4. Парні і непарні числа.
 Теоретичний матеріал
Теоретичний матеріал
Будь-яке натуральне число, запис якого закінчується цифрою 0, ділиться без остачі на 10. Щоб одержати частку, досить відкинути цифру 0.
Наприклад, 350 ділиться без остачі на 10, оскільки 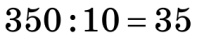 .
.
Якщо 353 поділити на 10, то отримаємо неповну частку 35 і в остачі 3 (тобто останню цифру запису цього числа). Тому, якщо в записі натурального числа останньою цифрою не є 0, то це число не ділиться без остачі на 10.
Якщо запис натурального числа закінчується цифрою 0, то це число ділиться без остачі на 10. Якщо запис натурального числа закінчується іншою цифрою, то воно не ділиться без остачі на 10.
Так, 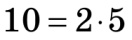 , тобто число ділиться на 2 і на 5 без остачі. З цього випливає, що будь-яке число, запис якого закінчується цифрою 0 , ділиться без остачі і на 5, і на 2.
, тобто число ділиться на 2 і на 5 без остачі. З цього випливає, що будь-яке число, запис якого закінчується цифрою 0 , ділиться без остачі і на 5, і на 2.
Наприклад, 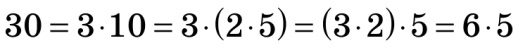 . Отже,
. Отже, 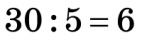 .
.
Кожне з чисел можна записати у вигляді суми повних десятків і одиниць.
Наприклад, 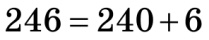 ;
; 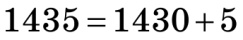 . Оскільки повні десятки діляться на 5, то і все число ділиться на 5 лише у тому випадку, коли на 5 ділиться число одиниць. Тобто тоді, коли в розряді одиниць маємо 0 або 5.
. Оскільки повні десятки діляться на 5, то і все число ділиться на 5 лише у тому випадку, коли на 5 ділиться число одиниць. Тобто тоді, коли в розряді одиниць маємо 0 або 5.
Якщо запис натурального числа закінчується цифрами 0 або 5, то це число ділиться без остачі на 5. Якщо ж запис числа закінчується іншою цифрою, то число на 5 без остачі не ділиться.
Наприклад, числа 950 і 955 діляться без остачі на 5, а число 952 — ні.
Числа, що діляться без остачі на 2, називають парними, а числа, які при діленні на 2 дають остачу 1, — непарними.
З одноцифрових чисел парними є 0; 2; 4; 6 і 8; непарними є 1; 3; 5; 7; 9. Тому цифри 0; 2; 4; 6; 8 називають парними, а цифри 1; 3; 5; 7; 9 — непарними.
Всі повні десятки діляться без остачі на 2. Отже, будь-яке натуральне число парне лише тоді, коли в розряді одиниць стоїть парна цифра.
Якщо запис натурального числа закінчується парною цифрою, то це число парне, а якщо запис числа закінчується непарною цифрою, то це число непарне.
Наприклад, 2; 80; 98; 506 — парні числа, а 5; 53; 89; 507 — непарні числа.
| Число a ділиться на | 2 | якщо закінчується | на парну цифру |
| 5 | на 0 або 5 |
| 10 | на 0 |
■ V. Первинне закріплення знань
Варіант № 1
1. Запишіть усі натуральні числа, що розташовані між числами 149 і 156 та діляться на 2, але не діляться на 5.
2. Із цифр 4, 0 і 5 складіть усі трицифрові числа, що діляться без остачі на:
а) 2; б) 10; в) 5.
Кожну з цифр у записі одного числа використовуйте один раз.
Варіант № 2
1. Чи можна, використовуючи тільки цифри 9 і 5, записати:
а) число, що кратне 10;
б) непарне число;
в) парне число;
г) число, що ділиться на 5?
2. Не виконуючи дій, визначте, чи ділиться на 2; 5; 10 добуток:
а) 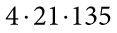 ; б)
; б) 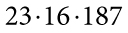 ; в)
; в) 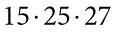 ..
..
Розв’язання до варіантів
Варіант № 1
1. Числа 152 і 254 діляться на 2 і не діляться на 5.
2. а) 450; 540; 504; б) 450; 540; в) 450; 540; 405.
Варіант № 2
1. а) Ні, оскільки за допомогою цифр 9 і 5 не можна записати число, що закінчується на 0;
б) так, 95 або 59;
в) ні, оскільки серед даних цифр немає парних;
г) так, 95.
2. а) добуток 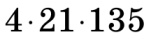 ділиться на 2, оскільки 4 кратне 2;
ділиться на 2, оскільки 4 кратне 2;
добуток 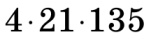 ділиться на 5, оскільки 135 кратне 5;
ділиться на 5, оскільки 135 кратне 5;
добуток 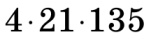 ділиться на 10, оскільки ділиться і на 2, і на 5.
ділиться на 10, оскільки ділиться і на 2, і на 5.
б) 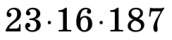 ділиться на 2, оскільки 16 кратне 2;
ділиться на 2, оскільки 16 кратне 2;
в) 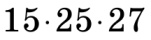 ділиться на 5, оскільки 15 і 25 кратні 5.
ділиться на 5, оскільки 15 і 25 кратні 5.
| ▪ Додатковий матеріал Для тих, хто цікавиться математикою! |
| Розгляньте ознаки подільності на 4 і 11. |
| Ознака подільності на 4 |
| Натуральне число, що містить не менше ніж три цифри, ділиться на 4 тоді і лише тоді, коли дві його останні цифри становлять число, що ділиться на 4. |
| Наприклад, число 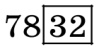 ділиться на 4, оскільки число 32 ділиться на 4. ділиться на 4, оскільки число 32 ділиться на 4. |
| Ознака подільності на 11 |
| Натуральне число ділиться на 11 тоді й лише тоді, коли різниця між сумою цифр, які займають непарні місця, і сумою цифр, які займають парні місця, ділиться на 11. |
| Наприклад, а) 482 31 ділиться на 11 тому що 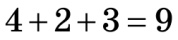 , , 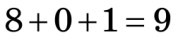 , ,  , 0; 11; , 0; 11; б) 3 528 041 ділиться на 11 тому, що 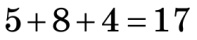 , , 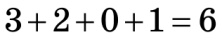 , , 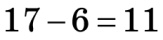 , 111; 11. , 111; 11. |
■ VI. Підбиття підсумків заняття
▪ Завдання
Допишіть до числа 131 праворуч таку цифру, щоб отримати число, яке ділиться на:
а) 2; в) 10;
б) 5; г)* 4 (для тих, хто цікавиться математикою).
 VIII. Додаткове завдання
VIII. Додаткове завдання
Купили 5 однакових коробок кольорових олівців. Чи може в них міститися разом 92 олівця; 90 олівців; 75 олівців?






 Словничок (глосарій):
Словничок (глосарій): Чи можна, не виконуючи ділення, а тільки за зовнішнім виглядом числа встановити, чи ділиться, наприклад, число 19348 на 2, число 917 595 на 5 або 10? На цьому занятті ми ознайомимося з правилами(ознаками), які підтвердять або спростують ваші припущення.
Чи можна, не виконуючи ділення, а тільки за зовнішнім виглядом числа встановити, чи ділиться, наприклад, число 19348 на 2, число 917 595 на 5 або 10? На цьому занятті ми ознайомимося з правилами(ознаками), які підтвердять або спростують ваші припущення. Теоретичний матеріал
Теоретичний матеріал VIII. Додаткове завдання
VIII. Додаткове завдання









