Применения интеграла к вычислению площадей и объемов

Тема: Применения интеграла к вычислению площадей и объемов

Цель- систематизировать и углубить знания по теме Применения интеграла к вычислению площадей и объемов

Содержание урока

1. Организационный момент. Приветствие. Проверка готовности к уроку.

2. Актуализация знаний:

Мозговой штурм:

1.  Давайте разберёмся, если функция задается в виде многочлена третьей степени, то какую степень имеет производная этой функции? А первообразная?

2.  Для какой функции производная совпадает с самой функцией?

3.  Производные каких функций равны 1, x, x²?

4.  Вспомним, какая функция называется первообразной для заданной функции на заданном промежутке?

5.  Если F(x) –первообразная для f(x), то каким равенством связаны они между собой?

6.  Какая из двух функций является первообразной другой: 5x⁴ и x⁵+11? Почему?

7.  Является ли функция F(x) = сtg x первообразной для функции f(x) = -1/sin² x на R?

8.  Как проверить результаты интегрирования?

1. Работа по теме урока

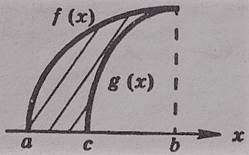
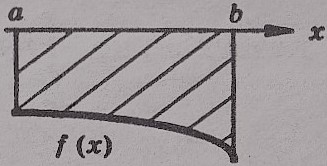
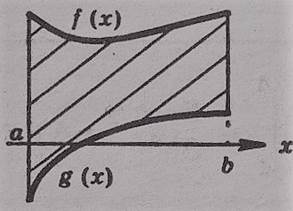
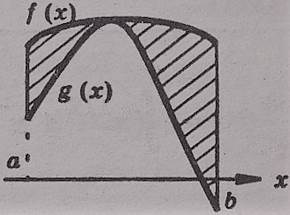
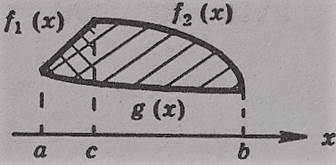
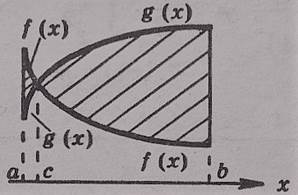
- Какая фигура называется криволинейной трапецией?

- фигура, ограниченная отрезками прямых х = а, х = b, у = 0 и графиком непрерывной функции

у = f (х), такой что f (х) ≥ 0 на отрезке [а;b] и f (х) 0 при х 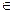  (а;b), называется криволинейной трапецией.

- Укажите номера чертежей, на которых представлена криволинейная трапеция:

 -Как вычислить площадь таких фигур?( по формуле :  )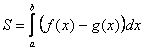

Задача

1. Вычислить площадь фигуры, ограниченной прямойy = x – 2 и параболой y = x² – 4x + 2.( совместное фронтальное решение)

2.  Вычислить площадь фигуры, ограниченной линиями y = x, y = 5 – x, x = 1, x = 2.( самостоятельное решение с последующей проверкой).

- Давайте вспомним какие еще практические задачи можно решать с помощью нахождения интеграла?

- Объёмы каких геометрических тел вы уже умеете находить?

Давайте вспомним на примере решения задачи:

Задача 1 Сечение тела плоскостью, перпендикулярной к оси 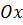  и проходящей через точку с абсциссой  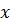, является квадратом, сторона которого равна  . Найти объем этого тела.( фронтальное решение)

Задача 2

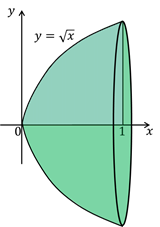
Найти объём тела, полученного вращением данной кривой вокруг оси  .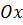

Задача 3: найти объём тела, полученного вращением данной кривой вокруг оси  .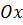

1. Итоги урока. Рефлексия.Домашнее задание.