г. Москва
2021 г.
Значение математической подготовки в становлении современного человека определяет следующие общие цели школьного математического образования: − овладение конкретными математическими знаниями, необходимыми для применения в практической деятельности, для изучения смежных дисциплин, для продолжения образования; − интеллектуальное развитие учащихся, формирование качеств мышления, характерных для математической деятельности; − формирование представлений об идеях и методах математики, о математике как форме описания и методе познания действительности; − формирование представлений о значимости математики как части общечеловеческой культуры в развитии цивилизации и в современном обществе.
Реализация этих целей на старшей ступени школы дифференцируется в зависимости от направленности интересов ученика. Для тех, кто предполагает учиться дальше, не испытывая трудностей с математическими обоснованиями и расчетами, необходимо осознавать свой выбор и прилагать максимум усилий к своему самообразованию. Этому может способствовать предлагаемый курс.
обобщение и систематизация, расширение и углубление знаний по математике.
− развитие алгоритмической культуры, логического мышления и интуиции; − развитие умений самостоятельно анализировать и решать нестандартные задачи; − расширение представления учащихся о математике как науке; − развитие коммуникативных и общеучебных навыков работы в группе, самостоятельной работы, умений вести дискуссию, аргументировать ответы; − подготовка учащихся к итоговой аттестации.
− текущий контроль (вопросы учащихся к учителю; индивидуальные и групповые беседы по изучающим вопросам; ответы и выступления учащихся в процессе занятия и т.д.);
− тематический контроль: самостоятельное решение предложенных задач с последующим разбором вариантов решений.
В технологии проведения занятий присутствует элемент самопроверки, который предоставляет учащимся возможность самим проверить, как ими усвоен изученный материал.
− повторить и систематизировать ранее изученный материал школьного курса математики; − освоить основные приемы решения задач; − овладеть навыками анализа и построения предполагаемого решения задачи; − познакомиться и использовать на практике нестандартные методы решения задач; − повысить уровень своей математической культуры, творческого развития, познавательной активности.
| № п/п | № п/т |
Содержание учебного материала
|
|
|
|
| I. Текстовые задачи (20 ч). |
|
|
|
| Задачи на движение (5 ч) |
|
| 1 | 1 | Движение по прямой дороге. |
|
| 2 | 2 | Движение по реке. |
|
| 3 | 3 | Движение по окружности. |
|
| 4 | 4 | Движение протяженных тел. |
|
| 5 | 5 | Средняя скорость. |
|
|
|
| Задачи на проценты (6 ч) |
|
| 6 | 1 | Задачи на проценты, техника их решения. |
|
| 7 | 2 | Распродажа. Тарифы. Штрафы. |
|
| 8 | 3 | Вычисление сложных процентов. |
|
| 9 | 4 | Определение величины вклада. Банковские операции. |
|
| 10 | 5 | Практикум по решению задач с экономическим содержанием. |
|
| 11 | 6 | Практикум по решению задач с экономическим содержанием. |
|
|
|
| Задачи на концентрацию (2 ч) |
|
| 12 | 1 | Задачи на сплавы, смеси, растворы. |
|
| 13 | 2 | Практикум по решению задач. |
|
|
|
| Задачи на работу (3 ч) |
|
| 14 | 1 | Задачи на явный объем работы. |
|
| 15 | 2 | Задачи на неявный объем работы. |
|
| 16 | 3 | Практикум по решению задач. |
|
|
|
| Другие задачи (4 ч) |
|
| 17 | 1 | Задачи на числа. |
|
| 18 | 2 | Задачи на арифметическую прогрессию. |
|
| 19 | 3 | Задачи на геометрическую прогрессию. |
|
| 20 | 4 | Практикум по решению задач. |
|
|
|
| Планиметрия ( 26 ч) |
|
|
|
| Метод ключевых задач (14 ч) |
|
| 21 | 1 | Параллельные прямые, пересекающие стороны угла. Середины сторон четырехугольника. |
|
| 22 | 2 | Медиана, проведенная к гипотенузе. Соотношения в прямоугольном треугольнике. |
|
| 23 | 3 | Вписанный угол. Угол между касательной и хордой. |
|
| 24 | 4 | Величина угла, вершина которого лежит внутри (вне) окружности. |
|
| 25 | 5 | Формула 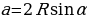 . . |
|
| 26 | 6 | Свойства пересекающихся хорд. |
|
| 27 | 7 | Касательная и секущая, проведенные к окружности из одной точки. |
|
| 28 | 8 | Отношение площадей треугольников, имеющих общую высоту (основание). |
|
| 29 | 9 | Отношение площадей подобных треугольников. |
|
| 30 | 10 | Площади треугольников, на которые четырехугольник разделен диагоналями. |
|
| 31 | 11 | Признак параллельности сторон четырехугольника. |
|
| 32 | 12 | Расстояние от вершины треугольника до точки касания вписанной окружности со стороной. |
|
| 33 | 13 | Свойство биссектрисы угла треугольника. |
|
| 34 | 14 | Признаки подобия треугольников. |
|
|
|
| Избранные методы и приемы решения планиметрических задач (4 ч) |
|
| 35 | 1 | Удлинение медианы. |
|
| 36 | 2 | Метод вспомогательной площади. |
|
| 37 | 3 | Метод вспомогательной окружности. |
|
| 38 | 4 | Метод координат, векторный метод. |
|
|
|
| Многовариантные геометрические задачи (8 ч) |
|
| 39 | 1 | Задачи, в которых условие задачи не определяет взаимное расположение точек и фигуры. |
|
| 40 | 2 | Задачи, в которых условие задачи не определяет взаимное расположение точек и фигуры. |
|
| 41 | 3 | Задачи, в условии которых фигурируют окружности. |
|
| 42 | 4 | Задачи, в условии которых фигурируют окружности. |
|
| 43 | 5 | Другие многовариантные геометрические задачи. |
|
| 44 | 6 | Другие многовариантные геометрические задачи. |
|
| 45 | 7 | Решение задач. |
|
| 46 | 8 | Решение задач. |
|
|
|
| Модуль (10 часов) |
|
| 47 | 1 | Модуль числа. Свойства модуля. |
|
| 48 | 2 | Раскрытие модуля из определения. |
|
| 49 | 3 | Метод интервалов – универсальный способ решения задач с модулями. |
|
| 50 | 4 | Важнейшие свойства модулей, использование которых существенно упрощает решение задач. |
|
| 51 | 5 | Приемы и методы, ускоряющие процесс решения некоторых классов задач с модулями. |
|
| 52 | 6 | Обобщение модели 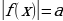 . Модель . Модель 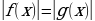 и её аналоги в неравенствах. и её аналоги в неравенствах. |
|
| 53 | 7 | Решение систем уравнений с модулем. |
|
| 54 | 8 | Построение графиков функций, содержащих модуль. |
|
| 55 | 9 | Учимся на чужих ошибках. |
|
| 56 | 10 | Решение более сложных задач. |
|
|
|
| Задачи с параметрами ( 12 ч) |
|
| 57 | 1 | Линейные уравнения и уравнения, приводимые к линейным. |
|
| 58 | 2 | Линейные неравенства и неравенства, приводимые к линейным. |
|
| 59 | 3 | Квадратные уравнения и уравнения, приводимые к квадратным. |
|
| 60 | 4 | Квадратные неравенства. |
|
| 61 | 5 | Квадратный трехчлен, расположение корней квадратного трехчлена. |
|
| 62 | 6 | Квадратный трехчлен, расположение корней квадратного трехчлена. |
|
| 63 | 7 | Графические приемы при решении. |
|
| 64 | 8 | Графические приемы при решении. |
|
| 65 | 9 | Параметр и количество решений уравнений, неравенств и их систем. |
|
| 66 | 10 | Параметр и количество решений уравнений, неравенств и их систем. |
|
| 67 | 11 | Уравнения и неравенства с параметрами с различными условиями. |
|
| 68 | 12 | Уравнения и неравенства с параметрами с различными условиями. |
|
Крамор В.С. «Повторяем и систематизируем школьный курс алгебры и начал анализа», М.: Просвещение, 1990.
Шарыгин И.Ф. «Факультативный курс по математике: решение задач». Учебное пособие для 10 класса средней школы. – М.: Просвещение, 1989.
Егерев В.К. и др. Сборник задач по математике. Под ред. М.И. Сканави. – 10-е изд.,. – М., «Мир и образование», 2005
Студенецкая В. Н., Гребнева З. С. «Решение задач и выполнение заданий с комментариями и ответами для подготовки к единому государственному экзамену». Часть 1.- Волгоград: Учитель, 2003
Бродский И.Л. «Решение экзаменационных заданий повышенной сложности по алгебре и началам анализа за курс средней школы». Пособие для учащихся и учителей. – М.: АРКТИ, 2001.
Туманов С.И. «Поиски решения задачи» − М.: Просвещение, 1969.
Субханкулова С.А. «Задачи с параметрами» − М.: ИЛЕКСА, 2010.
Лысенко Ф.Ф. и др. «Повышенный уровень ЕГЭ»− Ростов-на-Дону, Легион-М, 2014.
Шарыгин И.Ф. Решение задач: учеб. пособие для 10 кл. общеобразоват. учреждений. – М.: Просвещение, 1994.
Рабинович Е.М., Полонский В.Б. Учимся решать задачи по геометрии. Киев, 1996г.







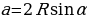 .
.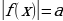 . Модель
. Модель 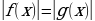 и её аналоги в неравенствах.
и её аналоги в неравенствах.









