Проект по теме "Приёмы быстрого счёта".

«Устный счет - гимнастика для ума»

Приемы быстрого счета

Выполнила: ученица 5 класса «Б»

Гладышева Елизавета.

Руководитель: учитель математики

Громова Татьяна Владимировна

Актуальность темы

• Устный счет – гимнастика для ума. Счет в уме является самым древним способом вычисления. Освоение вычислительных навыков развивает память и помогает усваивать предметы естественно-математического цикла.
• Существует много приемов упрощения арифметических действий. Знание упрощенных приемов вычисления особенно важно в тех случаях, когда вычисляющий не имеет в своем распоряжении таблиц и калькулятора.
• Я остановлюсь на способах сложения, вычитания, умножения, деления, для производства которых достаточно устного счета или применения ручки и бумаги.
• Мотивацией для выбора темы послужило желание продолжения формирования вычислительных навыков, умения быстро и чётко находить результат математических действий.
• Правила и приёмы вычислений не зависят от того, выполняются они письменно или устно. Однако, владение навыками устных вычислений представляет большую ценность не потому, что в быту ими пользуются чаще, чем письменными выкладками. Это важно ещё и потому, что они ускоряют письменные вычисления, дают выигрыш в вычислительной работе.

Актуальность темы

• Немногие умеют считать быстро и правильно. Говорят, если хотите научиться плавать, вы должны войти в воду, а если хотите уметь решать задачи, то должны начать их решать. Научиться считать быстро, считать в уме можно только при большом желании и систематической тренировке в решении задач.
• А ведь приёмы быстрого устного счёта известны давно. Великолепные способности к устному счёту таких блестящих математиков, как Гаусс, фон Нейман, Эйлер или Валлис, вызывают настоящий восторг. Об этом много написано. Я хочу рассказать и показать некоторые известные вычислительные секреты. И тогда перед вами откроется совсем другая математика. Живая, полезная и понятная.

Содержание

• Актуальность.
• Счёт на пальцах.
• Умножение чисел от 10 до 20.
• Умножение на 11.
• Умножение на 22, 33, …, 99.
• Умножение на 25.
• Умножение на 5, 50, 25, 125.
• Уменьшение и увеличение суммы в выражении.
• Умножение на число, оканчивающееся на 5.
• Вычитание из 1000.
• Способы быстрого сложения натуральных чисел.
• Способы быстрого вычитания натуральных чисел.
• Быстрое возведение в квадрат.
• Приём перекрёстного умножения (способом Ферроля) при действии с двузначными числами.
• Умножение однозначного или двузначного числа на 37.
• Легко запомнить!

Цель проекта

Изучить и научиться применять некоторые способы быстрого счета, для производства которых достаточно устного счета или применения ручки и бумаги.

1.

• Изучить литературу по данной теме.
• Изучить литературу по данной теме.

2.

• Освоить несколько быстрых и удобных способов устного счета, которые могут пригодиться в математике.
• Освоить несколько быстрых и удобных способов устного счета, которые могут пригодиться в математике.

3.

• Провести исследования среди школьников 5 – 10 классов.
• Провести исследования среди школьников 5 – 10 классов.

4.

• Сделать выводы по результатам исследования.
• Сделать выводы по результатам исследования.

Задачи проекта

Счёт на пальцах

Способ быстрого умножения чисел в пределах первого десятка на 9.   Допустим, нам нужно умножить 7 на 9.

Повернём руки ладонями к себе и загнём седьмой палец (начиная считать от большого пальца слева).

Число пальцев слева от загнутого будет равно десяткам, а справа - единицам искомого произведения.

Умножение чисел от 10 до 20

Можно очень просто умножать такие числа!

• К одному из чисел надо прибавить количество единиц другого, умножить на 10 и прибавить произведение единиц чисел.
• Пример 1. 16∙18=(16+8) ∙ 10+6 ∙ 8=288, или
• Пример 2. 17 ∙ 17=(17+7) ∙ 10+7 ∙ 7=289.

Умножение на 11

• Чтобы двузначное число, сумма цифр которого не превышает 10, умножить на 11, надо цифры этого числа раздвинуть и поставить между ними сумму этих цифр.

• Примеры:

72 ∙ 11 = 7 (7 + 2) 2 = 792;

35 ∙ 11 = 3 (3 + 5) 5 = 385.

• Чтобы умножить на 11 двузначное число, сумма цифр которого 10 или больше 10, надо мысленно раздвинуть цифры этого числа, поставить между ними сумму этих цифр, а затем к первой цифре прибавить единицу, а вторую и последнюю (третью) оставить без изменения.
• Пример .

94 ∙ 11 = 9 (9 + 4) 4 = 9 (13) 4 = (9 + 1) 34 = 1034.

Умножение на 22, 33, ..., 99

• Чтобы двузначное число умножить на 22, 33, ..., 99, надо этот множитель представить в виде произведения однозначного числа (от 2 до 9) на 11, то есть 44 = 4 ∙ 11; 55 = 5 ∙ 11 и т.д. Затем произведение первых чисел умножить на 11.
• Пример 1. 24 ∙ 22 = 24 ∙ 2 ∙ 11 = 48 ∙ 11 = 528
• Пример 2. 23 ∙ 33 = 23 ∙ 3 ∙ 11= 69 ∙ 11 = 759

Умножение на 25

• Чтобы умножить какое-нибудь число, нужно данное число разделить 4.
• Ответ - полные сотни, остаток – неполные (1, 2, 3 или 25, 50, 75).
• Пример. 135 ∙ 25=(135:4=100:4+35:4)=33 сотни, остаток 3 (или неполная (3/4)сотня – 75)=3375.

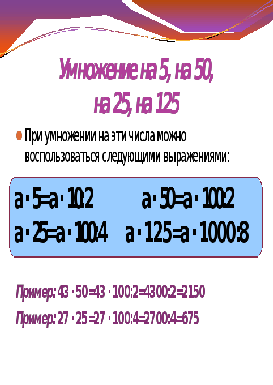
Умножение на 5, на 50, на 25, на 125

• При умножении на эти числа можно воспользоваться следующими выражениями:

a ∙ 5=a ∙ 10:2 a ∙ 50=a ∙ 100:2

a ∙ 25=a ∙ 100:4 а ∙ 125=а ∙ 1000:8

Пример: 43 ∙ 50=43 ∙ 100:2=4300:2=2150

Пример: 27 ∙ 25=27 ∙ 100:4=2700:4=675

a ∙ 5=a ∙ 10:2 a ∙ 50=a ∙ 100:2

a ∙ 25=a ∙ 100:4 а ∙ 125=а ∙ 1000:8

Увеличение и уменьшение суммы в выражении

• Если от суммы двух чисел отнять разность тех же чисел, то в результате получится удвоенное меньшее число, то есть (a+b)-(a-b)=2b
• Пример. (3+2)-(3-2)=2∙2=4
• Если к сумме двух чисел прибавить их разность, то получится удвоенное большее число, то есть

(a+b)+(a-b)=2a

• Пример. (3+2)+(3-2)=3 ∙ 2=6

Умножение на число, оканчивающиеся на 5

Чтобы четное двузначное число умножить на число, оканчивающееся на 5, можно применить следующее правило (срабатывает всегда).

Если один из сомножителей увеличить в несколько раз, а другой уменьшить во столько же раз, произведение не изменится.

Пример:

28 ∙ 15 = (28 : 4) ∙ (15 ∙ 4) = 7 ∙ 60 = 420.

Вычитание из 1000 (вы пришли в магазин с крупной купюрой)

Чтобы выполнить вычитание из 1000 и быстро рассчитать сдачу, можете пользоваться этим простым правилом:

Отнимите от 9 все цифры, кроме последней.

А последнюю цифру отнимите от 10!!!

Пример: 1000-648  Шаг1: от 9 отнимите 6 = 3  Шаг2: от 9 отнимите 4 = 5  Шаг3: от 10 отнимите 8 = 2  Ответ: 352

Способы быстрого сложения натуральных чисел

• Если одно из слагаемых увеличить на несколько единиц, а второе уменьшить на столько же единиц, то сумма не изменится.

Пример.

762+639=(762+8)+(639-8)=770 + 631=1401

Способы быстрого вычитания натуральных чисел

• Если вычитаемое уменьшить на несколько единиц и уменьшаемое увеличить на столько же единиц, то разность не изменится.

Пример:

529-435=(529-5)-(435+5)=524-440=84

Быстрое возведение в квадрат

• Этот прием поможет быстро возвести в квадрат двузначное число, которое заканчивается на 5. Умножьте первую цифру саму на себя +1, а в конце допишите 25. Вот и все! 

Пример:

25 2 = (2 ∙ (2+1)) добавляем 25  2 ∙ 3 = 6  625

Прием перекрестного умножения (способом Ферроля) при действии с двузначными числами

• Этот прием невероятно прост.
• Древние греки и индусы в старину называли его «способом молнии» или «умножение крестиком»

• Пример: 24 ∙ 32 = 768

Последовательно производим следующие действия:

1. 4 ∙ 2 = 8 – это последняя цифра результата.

2. 2 ∙ 2 = 4; 4 ∙ 3 = 12; 4 + 12 = 16.

6 – предпоследняя цифра в ответе, единицу запоминаем.

3. 2 ∙ 3 = 6, 6 + 1 = 7 – это первая цифра в ответе.

Ответ: 768.

Умножение однозначного или двузначного числа на 37

37 ∙ 3=111

37 ∙ 6=222

37 ∙ 9=333

37 ∙ 12=444

37 ∙ 15=555 и т.д

Легко запомнить!!!

7 ∙ 11 ∙ 13=1001

77 ∙ 13=1001

77 ∙ 26=2002

77 ∙ 39=3003 и т.д

Легко запомнить!!!

  11 ∙ 11 =121

111 ∙ 111 = 12321

1111 ∙ 1111 = 1234321

11111 ∙ 11111 =123454321

..........................

111111111 ∙ 111111111 = 12345678987654321

Ну-ка в сторону карандаши!

Ни костяшек. Ни ручек. Ни мела.

Устный счёт! Мы творим это дело

Только силой ума и души.

Числа сходятся где-то во тьме,

И глаза начинают светиться,

И кругом только умные лица,

Потому что считаем в уме.

Валентин Берестов (1928-1998)

Результаты исследования

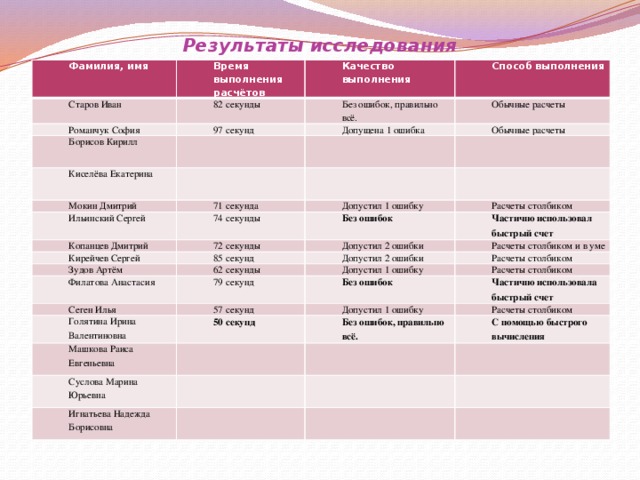
Фамилия, имя

Время выполнения расчётов

Старов Иван

Романчук София

Качество выполнения

82 секунды

97 секунд

Борисов Кирилл

Способ выполнения

Без ошибок, правильно всё.

Обычные расчеты

Допущена 1 ошибка

Киселёва Екатерина

Обычные расчеты

Мокин Дмитрий

71 секунда

Ильинский Сергей

Допустил 1 ошибку

Копанцев Дмитрий

74 секунды

Расчеты столбиком

72 секунды

Без ошибок

Кирейчев Сергей

Зудов Артём

85 секунд

Допустил 2 ошибки

Частично использовал быстрый счет

Расчеты столбиком и в уме

Филатова Анастасия

Допустил 2 ошибки

62 секунды

79 секунд

Сеген Илья

Допустил 1 ошибку

Расчеты столбиком

Расчеты столбиком

Без ошибок

57 секунд

Голятина Ирина Валентиновна

Частично использовала быстрый счет

Допустил 1 ошибку

50 секунд

Машкова Раиса Евгеньевна

Расчеты столбиком

Без ошибок, правильно всё.

Суслова Марина Юрьевна

С помощью быстрого вычисления

Игнатьева Надежда Борисовна

Выводы:

Существуют способы быстрого сложения, вычитания, умножения, деления, возведения в степень … Я рассмотрела лишь немногие способы быстрого счета.

Все рассмотренные мной методы устного вычисления говорят о многолетнем интересе ученых и простых людей к игре с цифрами. Используя некоторые из этих методов на уроках или дома, можно развить скорость вычислений, добиться успехов в изучении всех школьных предметов.

Использованные ресурсы:

• Арутюнян Е., Левитас Г. Занимательная математика.- М.: АСТ – ПРЕСС, 1999.
• Балк М.Б., Балк, Г.Д. Математика и ее история. – Москва. Просвещение, 1971.
• Волина В.В. Мир математики. – Ростов н/Д: Феникс, 1999.
• Гарднер М. Математические чудеса и тайны. – М., 1978.
• Депман И.Я. Возникновение системы мер и способов измерения величин. – Москва. Учпедгиз, 1956. – 136 с.
• Катлер Э. Мак-Шейн Р. Система быстрого счёта по Трахтенбергу.
• Перельман Я.И. Быстрый счёт. 30 простых приёмов устного счёта.
• Татарченко Т.Д. Способы быстрого счета на занятиях кружка, «Математика в школе», 2008, №7, стр.68
• http://www.superidea.ru Развитие творческого мышления и интеллекта
• http://www.all-fizika.com Техника быстрого счета. Быстрый счет в уме.

СПАСИБО ЗА ВНИМАНИЕ!!!