Управление образования Администрации
Дмитровского городского округа Московской области
МУНИЦИПАЛЬНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
КАТУАРОВСКАЯ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА
141865, Московская область, Дмитровский городской округ, рп. Некрасовский, ул. Парковая, д. 1
Тел: 8-496-222-40-47 (48), е-mail: [email protected] https://dmoukat.edumsko.ru/
ОКПО – 42277612; ОГРН – 1035001603691; ИНН/КПП - 5007029181 / 500701001

|
|
|
УТВЕРЖДАЮ |
|
|
| Директор МОУ Катуаровской СОШ |
|
|
| ___________________/Е.В.Филь/ |
|
|
| Приказом № 137/1«31» августа 2021 г.
|
Рабочая программа по учебному предмету
«Геометрия»
9Б класс
| Составила: |
| Шушпанова Е.В.. |
| учитель математики |
|
|
2021 год
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Рабочая программа по учебному предмету «Математика (геометрия)» для 9 класса составлена на основе федерального компонента государственного основного общего образования (2004), авторской программы по алгебре к учебнику для 9 класса общеобразовательной школы под редакцией А.Г. Мерзляк, В.Б. Полонский, М.С. Якир, Е.В.Буцко – М.: Вентана-граф, 2017. Основной образовательной программы МОУ Катуаровской СОШ.
Учебно-методический комплекс:
Учебник «Геометрия.9 класс» под ред. А.Г. Мерзляк, В.Б. Полонский, М.С. Якир, Е.В.Буцко – М.: Вентана-граф, 2017.
Дидактический материал «Геометрия. 9 класс» А.Г. Мерзляк, В.Б. Полонский, М.С. Якир (М.: Вентана-Граф 2017).
Общая характеристика учебного предмета
Геометрия-один из важнейших компонентов математического образования, необходимый для приобретения конкретных знаний о пространстве и практически значимых умений, формирования языка описания объектов окружающего мира, для развития пространственного воображения и интуиции, математической культуры, для эстетического воспитания учащихся. Изучение геометрии вносит вклад в развитие логического мышления, в формирование понятия доказательства.
Таким образом, в ходе освоения содержания курса учащиеся получают возможность развить пространственные представления и изобразительные умения, освоить основные факты и методы планиметрии, познакомиться с простейшими фигурами и их свойствами.
Курс характеризуется рациональным сочетанием логической строгости и геометрической наглядности.
Увеличивается теоретическая значимость изучаемого материала, расширяются внутренние логические связи курса, повышается роль дедукции, степень абстрактности изучаемого материала. Учащийся овладевает приёмами аналитико-синтетической деятельности при доказательстве теорем и решении задач. Изучение материала характеризуется постоянным обращением к наглядности, использованием рисунков и чертежей. Целенаправленное обращение к приемам из практики развивает умения вычислять геометрические факты, формы и отношения в предметах и явлениях деятельности.
В основу курса геометрии для 9 класса положены такие принципы как:
Целостность и непрерывность, означающие, что данная ступень является важным звеном единой общешкольной подготовки по математике.
Научность в сочетании с доступностью, строгость и систематичность изложения (включение в содержание фундаментальных положений современной науки с учетом возрастных особенностей обучаемых
Практико-ориентированность, обеспечивающая отбор содержания, направленного на решение простейших практических задач планирования деятельности, поиска нужной информации.
Принцип развивающего обучения (обучение ориентировано не только на получение новых знаний, но и активизацию мыслительных процессов, формирование и развитие у школьников обобщенных способов деятельности, формирование навыков самостоятельной работы).
Цели и задачи
Продолжить овладение системой геометрических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования.
Продолжить интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе; ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;
Формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
Воспитание культуры личности, отношение к геометрии как к части общечеловеческой культуры, понимание значимости геометрии для научно-технического прогресса.
В ходе преподавания геометрии в 9 классах, работы над формированием у учащихся перечисленных в программе знаний и умений следует обращать внимание на то, чтобы они овладевали умениями обще учебного характера, разнообразными способами деятельности, приобретали опыт:
планирования и осуществления алгоритмической деятельности, выполнения заданных и конструирования новых алгоритмов;
овладевали приемами аналитико-синтетической деятельности при доказательстве теории и решении задач;
целенаправленно обращались к примерам из практики, что развивает умения учащихся вычленять геометрические факты, формы и отношения в предметах и явлениях действительности, использовали язык геометрии для их описания, приобретали опыт исследовательской деятельности, развития идей, проведения экспериментов, обобщения, постановки и формулирования новых задач;
ясного, точного, грамотного изложения своих мыслей в устной и письменной речи; проведения доказательных рассуждений, аргументаций, выдвижения гипотез и их обоснования; поиска, систематизации, анализа и классификации информации, использования разнообразных информационных источников, включая учебную и справочную литературу, современные информационные технологии.
овладение системой математических знаний и умений, необходимых в практической деятельности, продолжения образования;
приобретение опыта планирования и осуществления алгоритмической деятельности;
освоение навыков и умений проведения доказательств, обоснования выбора решений;
приобретение умений ясного и точного изложения мыслей;
развить пространственные представления и умения, помочь освоить основные факты и методы планиметрии;
научить пользоваться геометрическим языком для описания предметов.
Обучение геометрии в основной школе направлено на достижение следующих целей:
в направлении личностного развития:
развитие логического и критического мышления, культуры речи, способности к умственному эксперименту;
формирование у учащихся интеллектуальной честности и объективности, способности к преодолению мыслительных стереотипов, вытекающих из обыденного опыта;
воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения;
формирование качеств мышления, необходимых для адаптации в современном информационном обществе;
развитие интереса к математическому творчеству и математических способностей;
в метапредметном направлении:
формирование представлений о математике как части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества;
развитие представлений о математике как форме описания и методе познания действительности, создание условий для приобретения первоначального опыта математического моделирования;
формирование общих способов интеллектуальной деятельности, характерных для математики и являющихся основой познавательной культуры, значимой для различных сфер человеческой деятельности;
в предметном направлении:
овладение геометрическим языком, умение использовать его для описания предметов окружающего мира; развитие пространственных представлений и изобразительных умений, приобретение навыков геометрических построений;
усвоение систематических знаний о плоских фигурах и их свойствах, а также на наглядном уровне — о простейших пространственных телах, умение применять систематические знания о них для решения геометрических и практических задач;
умение применять изученные понятия, результаты, методы для решения задач практического характера и задач из смежных дисциплин с использованием при необходимости справочных материалов, калькулятора, компьютера.
Место предмета в учебном плане
Учебный план МОУ Катуаровской СОШ предусматривает в 9 классе изучение предмета «Математика (геометрия)» в объеме 64 часов в год, по 2 часа в неделю 32 учебные недели. Данная рабочая программа в соответствии с календарным графиком школы на 2021-2022 учебный год рассчитана на 62 часа.
1.ПЛАНИРУЕМЫЕ РЕЗУЛЬТАТЫ ИЗУЧЕНИЯ УЧЕБНОГО ПРЕДМЕТА
Предметными результатами изучения курса является сформированность следующих умений:
пользоваться геометрическим языком для описания предметов окружающего мира;
распознавать геометрические фигуры, различать их взаимное расположение;
изображать геометрические фигуры; выполнять чертежи по условию задачи; осуществлять преобразования фигур;
проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования;
В результате изучения курса геометрии обучающиеся должны знать:
определения вектора и равных векторов;
какой вектор называется произведением вектора на число;
формулировки и доказательства леммы о коллинеарных векторах и теоремы о разложении вектора по двум неколлинеарным векторам, правила действий над векторами с заданными координатами;
как вводятся синус, косинус и тангенс углов от 0º до 180º; уметь доказывать основное тригонометрическое тождество;
формулы для вычисления координат точки;
вычислять длину отрезка по координатам его концов;
вычислять координаты середины отрезка;
использовать координатный метод для изучения свойств
прямых и окружностей.
определение правильного многоугольника;
знать теоремы об окружности, описанной около правильного многоугольника, и окружности, вписанной в правильный многоугольник;
формулы для вычисления угла, площади и стороны правильного многоугольника и радиуса вписанной в него окружности; формулы длины окружности и дуги окружности, площади круга и кругового сектора;
законы сложения векторов, определение разности двух векторов;
какой вектор называется противоположным данному;
определение движения плоскости.
Обучающиеся должны уметь:
объяснять, как определяется сумма двух и более векторов;
строить сумму двух и более данных векторов, пользуясь правилами треугольника, параллелограмма, многоугольника, строить разность двух данных векторов;
изображать и обозначать векторы, откладывать от данной точки вектор, равный данному;
выводить формулы координат вектора через координаты его конца и начала, координат середины отрезка, длины вектора и расстояния между двумя точками;
выводить уравнения окружности и прямой;
строить окружности и прямые, заданные уравнениями;
доказывать теорему о площади треугольника, теоремы синусов и косинусов;
объяснить, что такое угол между векторами; знать определение скалярного произведения векторов, условие перпендикулярности ненулевых векторов, выражение скалярного произведения в координатах и его свойства;
объяснить, что такое отображение плоскости на себя;
уметь доказывать, что осевая и центральная симметрии являются движениями и что при движении отрезок отображается на отрезок, а треугольник – на равный ему треугольник;
объяснить, что такое параллельный перенос и поворот;
доказывать, что параллельный перенос и поворот являются движениями плоскости;
формулировать свойства умножения вектора на число;
решать задачи.
расчетов, включающих простейшие тригонометрические формулы;
решения практических задач, связанных с нахождением геометрических величин (используя при необходимости справочники и технические средства);
построений геометрическими инструментами.
овладеть векторным методом для решения задач на вычисление и доказательство;
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
описания реальных ситуаций на языке геометрии;
решения геометрических задач с использованием тригонометрии;
расчетов, включающих простейшие тригонометрические формулы;
решения практических задач, связанных с нахождением геометрических величин (используя при необходимости справочники и технические средства);
построений геометрическими инструментами.
построений с помощью геометрических инструментов (линейка, угольник, циркуль, транспортир)
для решения несложных практических задач (например: размечать грядки различной формы);
для решения практических задач, связанных с нахождением периметра треугольника, измерением отрезков и углов, построением перпендикулярных и параллельных прямых
интерпретации результатов решения задач с учетом ограничений, связанных с реальными свойствами рассматриваемых процессов и явлений.
исследования (моделирования) несложных практических ситуаций на основе изученных формул и свойств фигур.
2.СОДЕРЖАНИЕ УЧЕБНОГО КУРСА
Глава 1. Решение треугольников (17 часов). Тригонометрические функции углов, теорема косинусов и теорема синусов. Решение треугольников. Формулы нахождения площади.
Глава 2. Правильные многоугольники (10 часов). Правильные многоугольники и их свойства, длина окружности. Площадь круга.
Глава 3. Декартовы координаты (12 часов). Расстояние между двумя точками с заданными координатами. Координаты середины отрезка. Уравнение фигуры. Уравнение окружности. Уравнение прямой. Угловой коэффициент прямой. Метод координат.
Глава 4. Векторы (15 часов). Понятие вектора. Координаты вектора. Сложение и вычитание векторов. Умножение вектора на число. Применение векторов. Скалярное произведение векторов.
Глава 5. Геометрические преобразования (8 часов). Движение(перемещение) фигуры. Параллельный перенос. Осевая симметрия. Центральная симметрия. Поворот. Гомотетия. Подобие фигур. Применение преобразования фигур при решении задач.
Формы организации учебных занятий, основных видов учебной деятельности:
фронтальная работа;
индивидуальная работа;
коллективная работа;
групповая работа;
рассказ;
объяснение;
лекция;
беседа;
применение наглядных пособий;
дифференцированные задания;
самостоятельная работа;
взаимопроверка;
дидактическая игра;
решение проблемно-поисковых задач.
3. КАЛЕНДАРНО-ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ
по учебному предмету «Математика (геометрия)» в 9 классе
на 62 часа (2 недельных часа по учебному плану)
на 2021-2022 учебный год
| № п/п | № урока в разделе |
Тема урока | Сроки проведения |
|
| по плану | по факту |
| ГЛАВА 1. Решение треугольников (17 ч) |
|
| 1 | 1 | Тригонометрические функции угла от 0°до 180° | 01.09-03.09.21 | 3 |
|
| 2 | 2 | Тригонометрические функции угла от 0°до 180°. Решение задач | 06.09-10.09 | 7 |
|
| 3 | 3 | Теорема косинусов | 06.09-10.09 | 10 |
|
| 4 | 4 | Теорема косинусов. Следствия из теоремы косинусов | 13.09-17.09 | 14 |
|
| 5 | 5 | Теорема косинусов. Решение ключевых задач | 13.09-17.09 | 17 |
|
| 6 | 6 | Теорема косинусов. Решение задач | 20.09-24.09 | 21 |
|
| 7 | 7 | Теорема синусов | 20.09-24.09 | 24 |
|
| 8 | 8 | Теорема синусов. Следствия из теоремы синусов | 27.09-01.10 | 28 |
|
| 9 | 9 | Применение теоремы синусов для решения задач. | 27.09-01.10 | 1 |
|
| 10 | 10 | Решение треугольников. 1 и 2 тип задач (по стороне и двум углам, по двум сторонам и углу между ними) | 11.10-15.10 | 12 |
|
| 11 | 11 | Решение треугольников. 3 и 4 тип задач (по трём сторонам, по двум сторонам и углу, противолежащему одной из сторон) | 11.10-15.10 | 15 |
|
| 12 | 12 | Формула для нахождения площади треугольника S=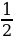 ab ab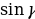 | 18.10-22.10 | 19 |
|
| 13 | 13 | Применение формул для нахождения площади треугольника при решении задач. | 18.10-22.10 | 22 |
|
| 14 | 14 | Формулы для нахождения площади треугольника (формула Герона, S= 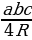 и S= pr) и S= pr) | 25.10-27.10 | 26 |
| 15 | 15 | Решение задач на вычисление площади треугольника по формулам. | 08.11-12.11 | 9 |
| 16
| 16 | Повторение и систематизация учебного материала по теме «Решение треугольников | 08.11-12.11 | 12 |
| 17 | 17 | Контрольная работа по теме «Решение треугольников» | 15.11-19.11 | 16.11 |
| ГЛАВА 2. Правильные многоугольники (10ч.) |
|
| 18 | 1 | Правильные многоугольники | 15.11-19.11 | 19 |
|
| 19 | 2 | Свойства правильных многоугольников | 22.11-26.11 | 23 |
| 20 | 3 | Формулы для нахождения радиусов описанной и вписанной окружностей правильного многоугольника | 22.11-26.11 | 26 |
| 21 | 4 | Построение правильных многоугольников | 29.11-03.12 | 30 |
| 22 | 5 | Длина окружности | 29.11-03.12 | 3 |
| 23 | 4 | Площадь круга | 06.12-10.12 | 7 |
| 24 | 7 | Длина окружности. Площадь круга. Решение задач. | 06.12-10.12 | 10 |
| 25 | 8 | Длина окружности. Площадь круга. Самостоятельная работа. | 13.12-17.12 | 14 |
| 26 | 9 | Повторение и систематизация учебного материала по теме «Правильные многоугольники» | 13.12-17.12 | 17 |
| 27 | 10 | Контрольная работа по теме «Правильные многоугольники» | 20.12-24.12 | 21.12 |
|
| ГЛАВА 3. Декартовы координаты (12ч.) |
|
| 28 | 1 | Расстояние между двумя точками с заданными координатами | 20.12-24.12 | 24 |
|
| 29 | 2 | Координаты середины отрезка | 27.12-30.12 | 28 |
| 30 | 3 | Расстояние между двумя точками с заданными координатами. Координаты середины отрезка. Решение задач | 10.01-14.01.22 | 11 |
| 31 | 4 | Уравнение фигуры | 10.01-14.01 | 14 |
| 32 | 5 | Уравнение окружности | 17.01-21.01 | 18 |
| 33 | 6 | Уравнение окружности. Решение задач | 17.01-21.01 | 21 |
| 34 | 7 | Уравнение прямой | 24.01-28.01 | 25 |
| 35 | 8 | Уравнение прямой. Решение задач | 24.01-28.01 | 28 |
| 36 | 9 | Угловой коэффициент прямой | 31.01-04.02 | 1 |
| 37 | 10 | Необходимое и достаточное условие параллельности прямых | 31.01-04.02 | 4 |
| 38 | 11 | Повторение и систематизация учебного материала по теме «Декартовы координаты» | 07.02-11.02 | 8 |
| 39 | 12 | Контрольная работа по теме «Декартовы координаты» | 07.02-11.02 | 11.02 |
| ГЛАВА 4. Векторы (15ч.) |
|
| 40 | 1 | Понятие вектора. Определение модуля вектора, равных векторов, противоположных векторов. | 14.02-18.02 | 15 |
|
| 41 | 2 | Понятие вектора. Решение задач | 14.02-18.02 | 18 |
|
| 42 | 3 | Координаты вектора | 28.02-04.03 | 1 |
|
| 43 | 4 | Сложение векторов | 28.02-04.03 | 4 |
| 44 | 5 | Вычитание векторов | 09.03-11.03 | 11 |
| 45 | 6 | Применение правила треугольника и параллелограмма для сложения векторов. Применение свойства сложения векторов, правила сложения векторов, заданных координатами, правила разности векторов, правила вычитания векторов, заданных координатами для решения задач. | 14.03-18.03 | 15 |
| 46 | 7 | Сложение и вычитание векторов. Обобщающий урок | 14.03-18.03 | 18 |
| 47 | 8 | Умножение вектора на число | 21.03-25.03 | 22 |
| 48 | 9 | Свойства коллинеарных векторов | 21.03-25.03 | 25 |
| 49 | 10 | Умножение вектора на число. Решение задач | 28.03-01.04 | 29 |
| 50 | 11 | Скалярное произведение векторов | 28.03-01.04 | 1 |
| 51 | 12 | Угол между векторами | 11.04-15.04 | 12 |
| 52 | 13 | Скалярное произведение векторов. Решение задач | 11.04-15.04 | 15 |
| 53 | 14 | Повторение и систематизация учебного материала по теме «Векторы» | 18.04-22.04 | 19 |
| 54 | 15 | Контрольная работа по теме «Векторы» | 18.04-22.04 | 22.04 |
| Глава 5. Геометрические преобразования (8ч) |
|
| 55 | 1 | Движение. Параллельный перенос Свойства параллельного переноса | 25.04-29.04 | 26 |
|
| 56 | 2 | Осевая симметрия | 25.04-29.04 | 29 |
| 57 | 3 | Центральная симметрия, поворот. | 04.05-06.05 | 6 |
| 58 | 4 | Гомотетия. Подобие фигур | 10.05-13.05 | 10 |
| 59 | 5 | Повторение и систематизация учебного материала по теме «Геометрические преобразования» | 10.05-13.05 | 13 |
|
| 60 | 6 | Контрольная работа по теме «Геометрические преобразования» | 16.05-20.05 | 17.05 |
| 61 | 7 | Анализ контрольной работы. Решение задач | 16.05-20.05 | 20 |
|
| 62 | 8 | Обобщение и систематизация знаний по курсу геометрии 9 класса. Итоговый урок | 23.05-24.05 | 24 |
|
| Рассмотрено на заседании ШМО | | Протокол от «31» августа 2021 г. № 1 | | Руководитель ШМО | | _______________/Антонова А.Г./ | | подпись расшифровка | | Согласовано | | заместитель директора по УВР | | _______________/Холкина А.И./ | | «31» августа 2021 г. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
30








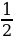 ab
ab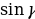
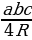 и S= pr)
и S= pr)









