Министерство образования и науки Республики Казахстан
Техническое и профессиональное образование
ГККП «Высший аграрно-технический колледж» УОАЗКО
Подготовила: преподаватель математики и физики
Казмагамбетова Катима Гайисовна
План открытого урока
По дисциплине: «Математика для экономистов»
Специальность: 0518000 «Учет и аудит (по отраслям)
Группа: СТ-111.2
Тема: «Вычисление пределов функции»
Компетенции:
Информационная:
Формировать умения и навыки вычисления пределов функции;
Познакомить учащихся со способами раскрытия неопределенностей 
Сформировать у учащихся навыки вычисления предела многочлена и отношения многочленов;
Развивать мышление учащихся при выполнении заданий;
Коммуникативная:
Формировать умения и навыки самостоятельно умственного труда;
Способствовать воспитанию дисциплинированности, усидчивости, навыков самостоятельности и умения работать индивидуально.
Решение проблем: сформировать умение и навыки при вычисления пределов функции
Тип урока: практическая работа.
Технологии: элементы информационно-коммуникационных технологий, технологии уровневой дифференциации.
Наглядные пособия и обеспечение процесса обучения:
Компьютер, мультимедийный проектор, презентация
Учебное пособие
карточки с заданиями
Формы работы учащихся: фронтальная, индивидуальная
Структура урока:
1. Организационный момент.
2. Сообщение темы занятия, актуализация опорных знаний.
3. Вычисление пределов функции.
4. Самостоятельные упражнения и проверка.
5. Подведение итогов урока.
6. Домашнее задание.
ХОД УРОКА
1. Организационный момент
Приветствие учителя, отметить отсутствующих, проверить подготовку к уроку. Сообщить тему и цель урока. В дальнейшем все задания выводятся на интерактивную доску.
2. Сообщение темы занятия, актуализация опорных знаний (3-5 минут)
Вычислим предел: 
Подставляем вместо х – 3.
Заметим, что предел числа равен самому числу.
Примеры: вычислите пределы 
Если в некоторой точке области определения функции существует предел и этот предел равен значению функции в данной точке, то функция называется непрерывной (в данной точке).

Вычислим значение функции в точке x0 = 3 и значение его предела в этой точке.

Значение предела и значение функции в этой точке совпадает, следовательно, функция непрерывна в точке x0 = 3.
Но при вычислении пределов зачастую появляются выражения, значение которых не определено. Такие выражения называют неопределённостями.

Основные виды неопределенностей: 
Раскрытие неопределенностей
Для раскрытия неопределенностей используют следующее:
упрощают выражение функции: раскладывают на множители, преобразовывают функцию с помощью формул сокращенного умножения, тригонометрических формул, домножают на сопряженное, что позволяет в дальнейшем сократить и т.д., и т.п.;
если предел при раскрытии неопределенностей существует, то говорят, что функция сходится к указанному значению, если такого предела не существует, то говорят, что функция расходится.
Пример: вычислим предел.
Разложим числитель на множители 

3. Вычисление пределов функции
Пример 1. Вычислите предел функции: 
При прямой подстановке, получается неопределенность:

Разложим на множители числитель и знаменатель и вычислим предел.

Пример 2. Вычислите предел функции: 
При прямой подстановке, получается неопределенность.

Помножим и числитель, и знаменатель на  .
.

Учтем, что если число разделить на бесконечно большое число получится ноль. То есть предел  Аналогично
Аналогично 

Пример 3. Вычислите предел функции: 
При прямой подстановке, получается неопределенность.

Помножим и числитель, и знаменатель на  .
.

Мы учли, что 
4. Самостоятельные упражнения и проверка.
Вычислите пределы:
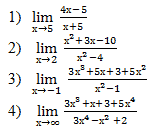
5. Подведение итогов урока
Данный урок по теме: «Вычисление пределов функции».
На уроке рассмотрены способы нахождения пределов. Разобрано что такое неопределенность, как раскрывать неопределенности. Надо заметить, что есть пределы, для которых невозможно найти числовое значение.
6. Домашнее задание
Домашнее задание раздается на карточках каждому ученику.
Вариант 1
При вычислении каких пределов будет получен ответ «2»?
Какие из нижеперечисленных пределов функций вычислены правильно:
А. 
В. 
С. 
Д. 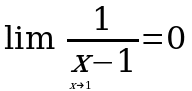
Выберите утверждения, справедливые для пределов функций:
А. Предел произведения функций равен произведению пределов
В. Постоянный множитель нельзя выносить за знак предела
С. Предел суммы функций равен сумме пределов
Д. Предел отношения функций равен разности пределов
Для раскрытия неопределенности 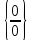 требуется:
требуется:
А. Разделить числитель и знаменатель на наивысшую степень x
В. Подставить значение x и рассчитать результат
С. Домножить числитель и знаменатель на сопряженное (числителю или знаменателю) выражение
Д. Разложить числитель и знаменатель на множители
Вычисление пределов
А. 
В. 
С. 
Д. 
Вариант 2
При вычислении каких пределов будет получен ответ «3»?
2.Какие из нижеперечисленных пределов функций вычислены правильно:
А. 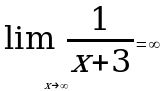
В. 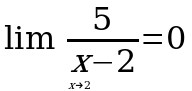
С. 
Д. 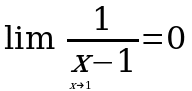
Выберите утверждения, справедливые для пределов функций:
А. Постоянный множитель можно вынести за знак предела
В. Предел произведения функций равен произведению пределов
С. Предел отношения функций равен отношению пределов
Д. Предел суммы функций равен произведению пределов
Для раскрытия неопределенности  требуется:
требуется:
А. Разделить числитель и знаменатель на наивысшую степень x
В. Подставить значение x и рассчитать результат
С. Домножить числитель и знаменатель на сопряженное (числителю или знаменателю) выражение
Д. Разложить числитель и знаменатель на множители
5.Вычисление пределов
А. 
В. 
С. 
Д. 
















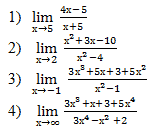













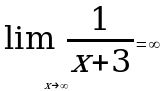
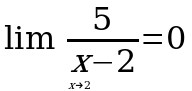

 требуется:
требуется:













