7 – сабак
Эки өзгөрүлмөлүү сызыктуу теңдемелер.
а∙х + в∙у = с теңдемеси эки өзгөрүлмөлүү сызыктуу теңдеме деп аталат. Координаталар системасында эки өзгөрүлмөлүү сызыктуу теңдемелердин графиктерин тургузууга болот жана алар түз сызыктар болушат.
а∙х + в∙у = с теңдемесинин графигин тургузуу үчүн анын графигинин координата октору менен кесилишүү ( у = 0 болсо, х = 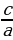 , ал эми х = 0 болсо, у =
, ал эми х = 0 болсо, у = 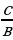 болот) чекиттерин табып алар аркылуу түз сызык жүргүзүү жетиштүү.
болот) чекиттерин табып алар аркылуу түз сызык жүргүзүү жетиштүү.
М: у = 3х − 2 сызыктуу теңдемесинин графигин тургузалы.
у = 0 болсо, х = 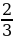 болот, ал эми х = 0 болсо, у = − 2 болот.
болот, ал эми х = 0 болсо, у = − 2 болот.
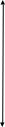 у
у
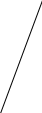
( 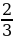 ;0)
;0)
0 х
х
(0; -2)
график тургузулду.
Эки өзгөрүлмөлүү сызыктуу теңдемелер системасы.
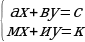 түрүндөгү система эки өзгөрүлмөлүү сызыктуу теңдемелер системасы деп аталат.
түрүндөгү система эки өзгөрүлмөлүү сызыктуу теңдемелер системасы деп аталат.
Эки өзгөрүлмөлүү эки теңдемелер системасын чыгарууда, алардын тамырларын:
ордуна коюу ыкмасы;
мүчөлөп кошуу ыкмасы;
өзгөрулмөнүн бирин жоюу ыкмасы;
графикалык ыкма ( графиктеринин кесилишүү чекиттери) аркылуу табууга болот.
Теңдемелер системасын чыгаруу ыкмаларына мисалдар карайлы.
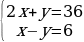 теңдемелер системасын чыгаргыла.
теңдемелер системасын чыгаргыла.
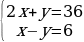 ордуна коюу ыкмасын колдонуп чыгаралы.
ордуна коюу ыкмасын колдонуп чыгаралы.
Чыгаруу:
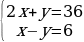 →
→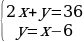 →
→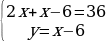 →
→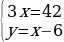 →
→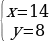 Жообу: (14; 8).
Жообу: (14; 8).
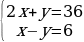 мүчөлөп кошуу аркылуу өзгөүлмөнүн бирин жоюу ыкмасын колдонуп чыгаралы.
мүчөлөп кошуу аркылуу өзгөүлмөнүн бирин жоюу ыкмасын колдонуп чыгаралы.
Чыгаруу:
2х + у = 36
+ х – у = 6
3х + 0 = 42 → х = 42/3 →х = 14
Экинчи тамырын х – у = 6 теңдемесинен у = х – 6 = 14 – 6 = 8 тамырын алабыз. Жообу (14;8)
2. (х + у) дин суммасы максималдуу болсо, теңдемелер системасынын маанилеринин суммасын тапкыла:
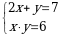
А) 5 Б) 6,5 В)7 Г) 5,5 Д) 9
3. Эгерде 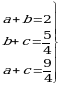 болсо, тапкыла
болсо, тапкыла 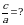
А) 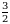 Б)
Б) 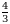 В)
В) 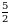 Г)
Г) 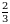 Д)
Д) 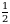
Эгерде 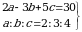 болсо, тапкыла
болсо, тапкыла 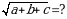
А) 1 Б) 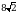 В)
В) 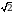 Г) 4 Д)
Г) 4 Д) 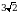
5. Эгерде 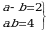 болсо, тапкыла
болсо, тапкыла 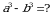
А) 16 Б) 24 В) 32 Г) 36 Д) 48
6. Эгерде 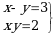 болсо, эсептегиле
болсо, эсептегиле 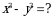
А) 5 Б)15 В)25 Г) 35 Д) 30
7. Эгерде 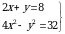 болсо, тапкыла (x,y) = ?
болсо, тапкыла (x,y) = ?
А) (3,4) Б) (5,-2) В) (4, 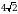 ) Г) (4,0) Д) (3,2)
) Г) (4,0) Д) (3,2)
Эгерде 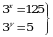 болсо,
болсо, 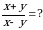 тапкыла.
тапкыла.
А) 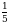 Б)
Б) 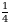 В)
В) 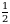 Г) 2 Д) 4
Г) 2 Д) 4
Эгерде 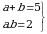 болсо, эсептегиле
болсо, эсептегиле 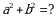
А)15 Б) 18 В)21 Г)25 Д) 30
Эгерде 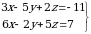 болсо x+y+z ти тапкыла ?
болсо x+y+z ти тапкыла ?
А) 1 Б) 2 В) 3 Г) 4 Д) 5
Эгерде 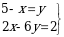 болсо, (х, y) ти тапкыла ?
болсо, (х, y) ти тапкыла ?
А) (-3,8) Б) (-3,1) В)(4,1) Г) (4,8) Д) (9,-4)
Эгерде 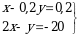 болсо, x + y ти тапкыла ?
болсо, x + y ти тапкыла ?
А) 21 Б)29 В) 41 Г) 48 Д) 51
Эгерде 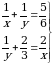 болсо, ( х , y) ти тапкыла ?
болсо, ( х , y) ти тапкыла ?
А) (1,3) Б) (1,6) В) (2,3) Г) (2,1) Д) (3,4)
Эгерде 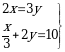 болсо, y ти тапкыла ?
болсо, y ти тапкыла ?
А) 1 Б) 2 В) 4 Г) 6 Д) 8
Эгерде 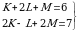 болсо, K + L + M ди тапкыла ?
болсо, K + L + M ди тапкыла ?
А) 1 Б) 2 В) 3 Г) 4 Д) 5
16.Теңдемелер системасын чыгар:
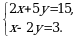
а)(5;2) б)(5;4) в)(5;1) г)(5;6) д)(5;11)
17. Теңдемелер системасы a нын кандай маанисинде чыгарылышка ээ эмес ?
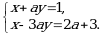 а)0 б)
а)0 б)  в)4 г)15 д)17
в)4 г)15 д)17
18. Теңдемелер системасы a нын кандай маанисинде чексиз көп чыгарылышка ээ болот ?
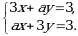 а)-3 б) 4 в)7 г)11 д)3
а)-3 б) 4 в)7 г)11 д)3
19. 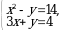 ( x + y ) эң чоң боло тургандай (x; y) тин маанилерин тапкыла.
( x + y ) эң чоң боло тургандай (x; y) тин маанилерин тапкыла.
A) 16 B) 24 C) 8 D) 22 E) -2
20. 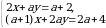 системасы a параметиринин кандай маанисинде чексиз көп чыгарылышка ээ болот ?
системасы a параметиринин кандай маанисинде чексиз көп чыгарылышка ээ болот ?
A) 1 B) 0 C) 3 D) -3 E) 7
21. 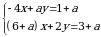 системасы a параметиринин кандай маанисинде чыгарылышка ээ болбойт ?
системасы a параметиринин кандай маанисинде чыгарылышка ээ болбойт ?
А) -9 Б) -8 В)-3 Г) -4 Д) 0
22. 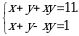 ( x + y ) эң чоң боло тургандай (x; y) тин маанилерин тапкыла.
( x + y ) эң чоң боло тургандай (x; y) тин маанилерин тапкыла.
А)7 Б) 9 В)0 Г)4 Д)6
Эгерде 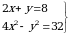 болсо, (x,y) ти тапкыла ?
болсо, (x,y) ти тапкыла ?
А) (3,4) Б) (5,-2) В) (4, 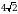 ) Г) (4,0) Д) (3,2)
) Г) (4,0) Д) (3,2)







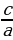 , ал эми х = 0 болсо, у =
, ал эми х = 0 болсо, у = 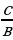 болот) чекиттерин табып алар аркылуу түз сызык жүргүзүү жетиштүү.
болот) чекиттерин табып алар аркылуу түз сызык жүргүзүү жетиштүү.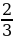 болот, ал эми х = 0 болсо, у = − 2 болот.
болот, ал эми х = 0 болсо, у = − 2 болот. у
у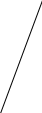
 х
х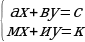 түрүндөгү система эки өзгөрүлмөлүү сызыктуу теңдемелер системасы деп аталат.
түрүндөгү система эки өзгөрүлмөлүү сызыктуу теңдемелер системасы деп аталат.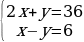 теңдемелер системасын чыгаргыла.
теңдемелер системасын чыгаргыла.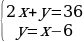 →
→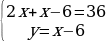 →
→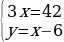 →
→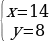 Жообу: (14; 8).
Жообу: (14; 8).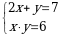
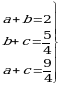 болсо, тапкыла
болсо, тапкыла 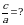
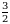 Б)
Б) 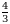 В)
В) 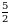 Г)
Г) 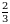 Д)
Д) 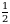
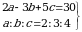 болсо, тапкыла
болсо, тапкыла 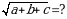
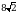 В)
В) 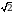 Г) 4 Д)
Г) 4 Д) 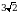
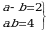 болсо, тапкыла
болсо, тапкыла 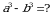
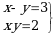 болсо, эсептегиле
болсо, эсептегиле 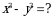
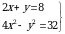 болсо, тапкыла (x,y) = ?
болсо, тапкыла (x,y) = ?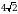 ) Г) (4,0) Д) (3,2)
) Г) (4,0) Д) (3,2)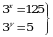 болсо,
болсо, 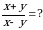 тапкыла.
тапкыла.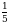 Б)
Б) 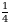 В)
В) 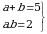 болсо, эсептегиле
болсо, эсептегиле 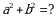
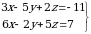 болсо x+y+z ти тапкыла ?
болсо x+y+z ти тапкыла ?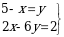 болсо, (х, y) ти тапкыла ?
болсо, (х, y) ти тапкыла ?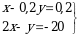 болсо, x + y ти тапкыла ?
болсо, x + y ти тапкыла ?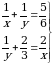 болсо, ( х , y) ти тапкыла ?
болсо, ( х , y) ти тапкыла ?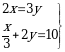 болсо, y ти тапкыла ?
болсо, y ти тапкыла ?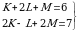 болсо, K + L + M ди тапкыла ?
болсо, K + L + M ди тапкыла ?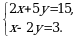
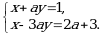 а)0 б)
а)0 б)  в)4 г)15 д)17
в)4 г)15 д)17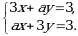 а)-3 б) 4 в)7 г)11 д)3
а)-3 б) 4 в)7 г)11 д)3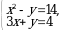 ( x + y ) эң чоң боло тургандай (x; y) тин маанилерин тапкыла.
( x + y ) эң чоң боло тургандай (x; y) тин маанилерин тапкыла. 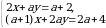 системасы a параметиринин кандай маанисинде чексиз көп чыгарылышка ээ болот ?
системасы a параметиринин кандай маанисинде чексиз көп чыгарылышка ээ болот ?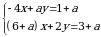 системасы a параметиринин кандай маанисинде чыгарылышка ээ болбойт ?
системасы a параметиринин кандай маанисинде чыгарылышка ээ болбойт ?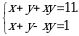 ( x + y ) эң чоң боло тургандай (x; y) тин маанилерин тапкыла.
( x + y ) эң чоң боло тургандай (x; y) тин маанилерин тапкыла.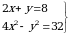 болсо, (x,y) ти тапкыла ?
болсо, (x,y) ти тапкыла ?









