В линейной алгебре линейная зависимость — это свойство, которое может иметь подмножество линейного пространства.
При линейной зависимости существует нетривиальная линейная комбинация элементов этого множества, равная нулевому элементу.
Как определить линейную независимость?
Система векторов является линейно независимой тогда и только тогда, когда в ней ни один вектор линейно не выражается через остальные векторы этой системы.
Как определить линейную зависимость матрицы?
Если ранг матрицы меньше числа ее строк (столбцов), то ее строки (столбцы) линейно зависимы. Если равен числу ее строк (столбцов), то строки (столбцы) линейно независимы.

Просмотр содержимого документа
«Линейная зависимость векторов»
Линейная зависимость Пусть 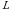 произвольное линейное пространство. Перенесём в него знакомое из векторной алгебры понятие линейной зависимости векторов.
произвольное линейное пространство. Перенесём в него знакомое из векторной алгебры понятие линейной зависимости векторов.
Определение. Векторы 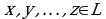 называются линейно зависимыми, если существуют такие числа
называются линейно зависимыми, если существуют такие числа 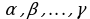 , не все одновременно равные нулю, что линейная комбинация данных векторов с этими числами даёт нулевой вектор пространства
, не все одновременно равные нулю, что линейная комбинация данных векторов с этими числами даёт нулевой вектор пространства 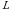 :
:
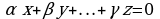 (1)
(1)
Векторы 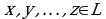 называются линейно независимыми, если равенство (1) выполняется только при
называются линейно независимыми, если равенство (1) выполняется только при 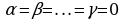 .
.
Рассмотрим несколько примеров.
Пример 1. Показать, что в пространстве 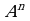 (
(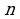 -мерном координатном пространстве) векторы
-мерном координатном пространстве) векторы
 (2)
(2)
линейно независимы.
Решение. Действительно, линейная комбинация векторов (2) с числами 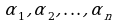 в силу аксиом линейного пространства представляет собой вектор
в силу аксиом линейного пространства представляет собой вектор 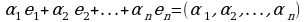 , который является нулевым лишь при условии
, который является нулевым лишь при условии 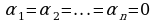 . ♦
. ♦
Пример 2. Рассмотреть вопрос о линейной зависимости в 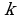 -мерном координатном пространстве
-мерном координатном пространстве 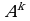 произвольных
произвольных 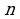 векторов
векторов
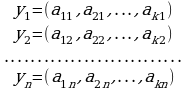 (3)
(3)
Решение. Равенство нулю линейной комбинации этих векторов с числами 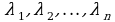
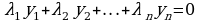 , (4)
, (4)
записанное в координатной форме, приводит к однородной системе 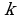 линейных уравнений относительно
линейных уравнений относительно 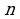 неизвестных
неизвестных 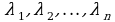 :
:
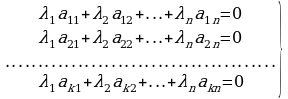 . (5)
. (5)
Однородная система (5) всегда имеет тривиальное решение
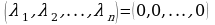 .
.
Если тривиальное решение является единственным, т.е. система (5) а с ней и равенство (4) удовлетворяется только с нулевым набором чисел 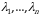 , то векторы
, то векторы 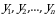 линейно независимы. Если же система (5) нетривиально совместна, т.е. кроме тривиального существует решение
линейно независимы. Если же система (5) нетривиально совместна, т.е. кроме тривиального существует решение
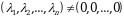 ,
,
то векторы 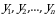 линейно зависимы. Иначе: линейная зависимость
линейно зависимы. Иначе: линейная зависимость 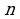 векторов в пространстве
векторов в пространстве 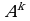 и нетривиальная совместность однородной системы
и нетривиальная совместность однородной системы 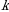 линейных уравнений с
линейных уравнений с 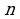 неизвестными это две стороны одной медали. ♦
неизвестными это две стороны одной медали. ♦








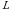 произвольное линейное пространство. Перенесём в него знакомое из векторной алгебры понятие линейной зависимости векторов.
произвольное линейное пространство. Перенесём в него знакомое из векторной алгебры понятие линейной зависимости векторов.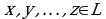 называются линейно зависимыми, если существуют такие числа
называются линейно зависимыми, если существуют такие числа 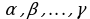 , не все одновременно равные нулю, что линейная комбинация данных векторов с этими числами даёт нулевой вектор пространства
, не все одновременно равные нулю, что линейная комбинация данных векторов с этими числами даёт нулевой вектор пространства 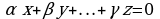 (1)
(1)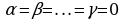 .
.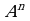 (
(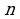 -мерном координатном пространстве) векторы
-мерном координатном пространстве) векторы (2)
(2)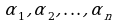 в силу аксиом линейного пространства представляет собой вектор
в силу аксиом линейного пространства представляет собой вектор 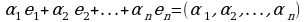 , который является нулевым лишь при условии
, который является нулевым лишь при условии 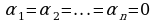 . ♦
. ♦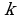 -мерном координатном пространстве
-мерном координатном пространстве 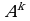 произвольных
произвольных 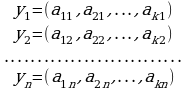 (3)
(3)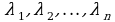
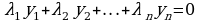 , (4)
, (4)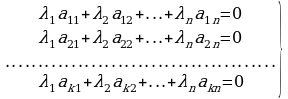 . (5)
. (5)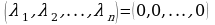 .
.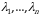 , то векторы
, то векторы 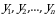 линейно независимы. Если же система (5) нетривиально совместна, т.е. кроме тривиального существует решение
линейно независимы. Если же система (5) нетривиально совместна, т.е. кроме тривиального существует решение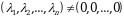 ,
,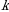 линейных уравнений с
линейных уравнений с 









