Занятие 58. Тема «Линейные и однородные дифференциальные уравнения. Методы их решения»
План лекции:
Линейные дифференциальные уравнения
Метод решения линейных ДУ
Однородные дифференциальные уравнения
Метод решения однородных ДУ
Линейные дифференциальные уравнения
Линейное дифференциальное уравнение первого порядка – это уравнение вида 
1) В линейное уравнение входит первая производная  или
или  .
.
2) В линейное уравнение входит произведение  , где
, где  - функция, а
- функция, а  – выражение, зависящее только от х.
– выражение, зависящее только от х.
3) И, наконец, в линейное уравнение входит выражение 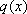 , тоже зависящее только от х. В частности,
, тоже зависящее только от х. В частности, 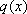 может быть константой.
может быть константой.
Метод решения линейных ДУ (алгоритм)
Линейное дифференциальное уравнение можно решить одной-единственной заменой:  , где
, где  и
и  – некоторые, пока ещё неизвестные функции, зависящие от х.
– некоторые, пока ещё неизвестные функции, зависящие от х.
Коль скоро проводится замена  , то нужно выяснить, чему равна производная. По правилу дифференцирования произведения:
, то нужно выяснить, чему равна производная. По правилу дифференцирования произведения: 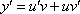
Подставляем  и
и 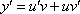 в наше уравнение, получим
в наше уравнение, получим

Далее нужно сгруппировать два слагаемых, которые содержат u, и вынесем его за скобку. Получим  (*)
(*)
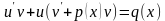
Затем, используя условие  , решим это уравнение, как уравнение с разделяющимися переменными. В итоге должны получить переменную
, решим это уравнение, как уравнение с разделяющимися переменными. В итоге должны получить переменную  , без добавления С в конце, то есть
, без добавления С в конце, то есть 
Далее полученное  подставляем в уравнение (*). Получаем,
подставляем в уравнение (*). Получаем,
 – тоже уравнение с разделяющимися переменными. Его необходимо решить, используя u
– тоже уравнение с разделяющимися переменными. Его необходимо решить, используя u , в итоге найдем u с добавлением С в конце. Затем полученные u и v подставить в замену
, в итоге найдем u с добавлением С в конце. Затем полученные u и v подставить в замену  , получим общее решение данного уравнения.
, получим общее решение данного уравнения.
Пример1. Решить уравнение: 
Решение.
Пусть  и
и 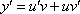 . Тогда уравнение примет вид
. Тогда уравнение примет вид

 (*)
(*)


 проинтегрируем
проинтегрируем


 =x
=x
Далее возвращаемся к уравнению (*), подставляем туда  =x, получаем
=x, получаем


du=dx проинтегрируем
 =
=
u=x+c
Таким образом, общее уравнение данного уравнения будет иметь вид
y=uv=(x+c)x=x2+xc
Однородные дифференциальные уравнения
Однородное дифференциальное уравнение первого порядка - это уравнение вида  , где f – функция.
, где f – функция.
Однородное дифференциальное уравнение первого порядка может иметь вид  , если
, если  и
и  - однородные функции одной и то же степени.
- однородные функции одной и то же степени.
Функция  называется однородной функцией k-й степени, если для любого t выполняется равенство
называется однородной функцией k-й степени, если для любого t выполняется равенство  . В частном случае, если однородная функция имеет нулевую степень, то выполняется равенство
. В частном случае, если однородная функция имеет нулевую степень, то выполняется равенство 
Метод решения однородных ДУ(алгоритм)
Для решения однородных ДУ первого порядка применяется следующая замена y=tx ( ) и dy=tdx+xdt.
) и dy=tdx+xdt.
Если уравнение содержит  , то необходимо сначала представить её в виде
, то необходимо сначала представить её в виде 
 , затем умножить обе части уравнения на dx, чтобы избавится от дроби., затем производить замену.
, затем умножить обе части уравнения на dx, чтобы избавится от дроби., затем производить замену.
Если уравнение не содержит  , а имеет вид
, а имеет вид , то сразу нужно вводить замену.
, то сразу нужно вводить замену.
После этих манипуляций, раскрыть все скобки, привести подобные слагаемые. Затем перенести в левую сторону все, что содержит dt, а в правую – что содержит dx. В итоге должны получить уравнение с разделяющимися переменными и решить его известным способом.
Пример 2. Решить уравнение
Решение.
Пусть y=tx и dy=tdx+xdt . Тогда уравнение примет вид
Раскроем скобки и приведем подобные слагаемые
Перенесем в левую сторону всё, что содержит dt, а в правую – что содержит dx. Получим

Вынесем в левой части за скобки всё, что можно
Получили уравнение с разделяющимися переменными. Перенесем в левую часть все, что с  , а в правую с х. Получим
, а в правую с х. Получим
Проинтегрируем 
Вернемся к замене  , . Это и есть общий интеграл данного уравнения.
, . Это и есть общий интеграл данного уравнения.
Задание на самостоятельную работу
- Ответить на контрольные вопросы письменно:
Какое уравнение называется линейным дифференциальным уравнением?
К какой замене сводится решение линейное ДУ?
Какое уравнение называют однородным дифференциальным уравнением?
К какой замене сводится решение однородного ДУ?
- Пользуясь этим и теоретическим материалом учебника П.Е. Данко «Высшая математика в упражнениях и задачах» часть 2 глава IV §1 п.3 стр.123 и п.6 стр.130, решить следующие ДУ:
1. 
2. 







 или
или  .
.
 (*)
(*)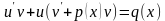
 , решим это уравнение, как уравнение с разделяющимися переменными. В итоге должны получить переменную
, решим это уравнение, как уравнение с разделяющимися переменными. В итоге должны получить переменную  , без добавления С в конце, то есть
, без добавления С в конце, то есть 
 – тоже уравнение с разделяющимися переменными. Его необходимо решить, используя u
– тоже уравнение с разделяющимися переменными. Его необходимо решить, используя u , в итоге найдем u с добавлением С в конце. Затем полученные u и v подставить в замену
, в итоге найдем u с добавлением С в конце. Затем полученные u и v подставить в замену 









