
Отдел образования администрации городского округа город Уфа
Муниципальное общеобразовательное учреждение
Башкирский лицей №2
Секция: математика
Номинация: геометрия
ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА
по теме
Лист Мёбиуса

Выполнила: Кулукаева Гузель 8 Б класс,
МОУ БЛ №2 Ленинского района городского округа город Уфа
Руководитель: Бареева Венера Самигулловна
учитель математики высшей категории
Уфа- 2009
Уфа- 2008
Анаш 2007
Оглавление
Введение …………………………………………………………………….... 3
Глава 1. А. Ф. Мёбиус и его открытие..........................................................4
1.1.А.Ф.Мёбиус и его поразительное открытие…………………………………….4
1.2.Что такое топология?............................................................................................4
1.3 Изготовление модели………………………………………………………….5.
Глава 2.Сюрпризы листа Мёбиуса...............................................................6
2.1.Знаменитое бумажное кольцо……………………………………....................6
2.2.Методика определения свойств листа Мёбиуса…..........................................6
2.3.Эксперименты и полученные результаты……………………………………6
Глава 3. Применение листа Мёбиуса............................................................8
Заключение………………………………………………………………….....10
Список использованной литературы………………………………………11
ВВЕДЕНИЕ
Мы решили показать, что математика полна неожиданностей, на примере открытия Августа Фердинанда Мёбиуса его знаменитого бумажного кольца с сюрпризами.
Моя работа посвящена изучению и исследованию свойств, а также практического применения листа Мебиуса в науке, технике, литературе и искусстве.
В повседневной жизни мы также встречаемся с данной поверхностью, хотя и не всегда догадываемся об этом.
Работа содержит результаты исследования, поиска и изучения материала.
Цель работы:
Определить и опытно – экспериментальным путём
проверить удивительные свойства ленты Мёбиуса.
- разработать методику определения удивительных свойств листа Мёбиуса;
Мы предполагаем, что лист Мёбиуса, как топологическая фигура, обладает действительно неожиданными свойствами.
Отсюда, объект исследования: лист Мёбиуса как модель односторонней поверхности.
Предмет исследования: свойства односторонний поверхности на примере ленты Мёбиуса.
Метод исследования: практический эксперимент.
Теоретическая значимость моей работы в том, что в последнее столетие большое влияние на ряд совершенно различных областей знания оказывает новая ветвь геометрии - топология. В наше время эта наука бурно развивается и находит применение в различных областях. Однако ей не уделяется должного внимания в школьном курсе геометрии.
Глава 1.А.Ф. Мёбиус и его поразительное открытие
1.1. Мёбиус Август Фердинанд

Таинственный и знаменитый лист Мёбиуса (иногда говорят лента Мёбиуса) открыл в1858 г. немецкий геометр Август Фердинанд Мёбиус (1790-1868), ученик «короля математиков» Гаусса. Мёбиус был первоначально астрономом, как Гаусс и многие другие из тех, кому математика обязана своим развитием. А.Ф. Мёбиус был разносторонним ученым. Он сделал много интересных открытий, стал одним из крупнейших геометров Х1Х в.
В возрасте 68 лет он сделал поразительное открытие - односторонние поверхности, одна из которых - лист Мёбиуса. Мёбиус является одним из основателей современной топологии.
1.2.Что такое топология?
Лист Мёбиуса - один из объектов топологии. Топология- «геометрия положения». У этого листа есть удивительные свойства: он имеет один край, одну сторону. Данные свойства не связаны с его положением в пространстве, с понятием расстояния, угла и, тем не менее, они имеют геометрический характер. Изучением этих свойств занимается топология.
В топологии изучаются свойства фигур и тел, которые не меняются при их непрерывных деформациях (как если бы они были сделаны из резины). С точки зрения топологии баранка и кружка – это одно и то же. Сжимая и растягивая кусочек резины, можно перейти от одного из этих тел ко второму. А вот баранка и шар – разные объекты, чтобы сделать отверстие, надо разорвать резину. Любую фигуру тополог имеет право сгибать, скручивать, сжимать и растягивать – делать с ней всё что угодно, только не разрывать и не склеивать. И при этом он будет считать, что ничего не произошло, все её свойства остались неизменными. Для него не имеют никакого значения ни расстояния, ни углы, ни площади
Среди букв русского алфавита есть топологически одинаковые фигуры А-Д, Г-С, С-П, Л-И, 3-Э, Т-У. Понятие и теоремы топологии полезны во всех областях математики, в технике, в экономике, психологии.
Топология – одна из наук, в которых не решены многие проблемы. Быть может, кто-то внесёт свой вклад в её развитие.
1.3 Изготовление модели.
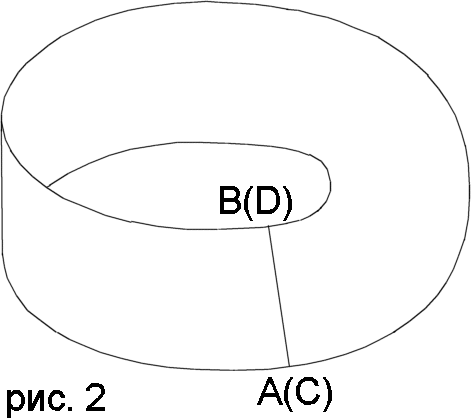
Лист Мебиуса- поверхность, получающаяся при склеивании двух противоположных сторон АВ и DC прямоугольника АВСD так, что точки А и В совмещаются соответственно с точками С и D. Другими словами ленту Мёбиуса легко получить, если соединить два конца ленты, но, соединяя, повернуть один из концов на 180 градусов относительно другого.

Глава 2. Сюрпризы листа Мёбиуса
2.1 Знаменитое бумажное кольцо
Лист Мебиуса, как топологическая фигура, обладает действительно неожиданными свойствами.
Лист Мёбиуса имеет ОДИН край.

Чтобы убедиться в этом, нужно выбрать в любом месте края листа Мёбиуса точку и перемещать её вдоль края. В результате мы придём в то же самое выбранное место.
Попробуем закрасить перекрученную ленту в два цвета – одним с внутренней стороны, а другим с внешней. Что бы вы ни придумывали, вам это не удастся.
Итак, это модель односторонней поверхности. В геометрическом, разумеется, понимании этого слова, потому что в нашем общечеловеческом смысле трудно представить более разностороннюю геометрическую фигуру.

До сих пор речь шла всего об одном свойстве листа Мёбиуса – о его односторонности. А ведь у него есть и другие подобные свойства. Но какие подобные? Математик назвал бы их топологическими.
2.2 Методика определения свойств листа Мёбиуса
Для определения необычных свойств листа Мёбиуса нами использована методика, в основе которой лежат опыты, предложенные Кордемским Б.А. [4 ]:
1.Какой формы можно взять бумажную полоску, чтобы склеить ленту Мёбиуса?
а) бумагу нельзя мять;
б) бумагу не запрещается мять;
2. Что произойдёт с этим бумажным кольцом, если его разрезать
на 1,2,3…одинаковых полосок?
3. Что получится, если перед склейкой:
а) ленту перекрутить дважды, а затем разрезать на две, три части?
б) ленту перекрутить трижды, а затем разрезать также на две или
три части?
2.3. Эксперименты и полученные результаты
1) Результаты опыта:
а) если бумагу нельзя мять, то лист Мёбиуса можно склеить только из прямоугольной полоски, где длина больше ширины. б) если бумагу не запрещается мять, то ленту Мёбиуса можно склеить не только из квадрата, но и из прямоугольника любых размеров – склеиваемые стороны могут быть во сколько угодно раз длиннее не склееваемых.
Сделать это можно так. Сложим прямоугольный лист в гармошку, перегнув его чётное число раз. Затем из этой гармошки, как из толстой бумажной полоски, склеим ленту Мёбиуса, вставляя, соответствующие части гармошки друг в друга. Лента Мёбиуса склеена, но лист бумаги оказался смятым.
2)Результаты второго опыта
| На сколько полосок разрезан лист Мёбиуса. | Что получилось после разрезания листа Мёбиуса.
|
|
2 | большие | маленькие |
| 1 |
|
| 3 | 1 | 1 |
| 4 | 2 |
|
| 5 | 2 | 1 |
| 6 | 3 |
|
| 7 | 3 | 1 |
| 8 | 4 |
|
| 9 | 4 | 1 |
| 10 | 5 |
|
- при разрезании ленты Мёбиуса на чётное число полосок получаются только большие сцепленные кольца, которых в два раза меньше, чем количество разрезов (полосок).


-при разрезании ленты Мёбиуса на нечётное число полосок получаются одно маленькое и несколько больших колец, сцепленных с маленьким, которых тоже в 2 раза меньше разности между количеством разрезов и маленьких колец.


3)Результаты третьего опыта.
| Количество разрезов | Количество полученных колец |
|
| Перекручено дважды | Перекручено трижды |
| 2 | 2 | 2 |
| 3 | 3 | 3 |
| 4 | 4 | 4 |
| 5 | 5 | 5 |
| 6 | 6 | 6 |
- если ленту перекрутить дважды и разрезать на четное или нечетное число полосок, то их количество совпадет с количеством получившихся взаимосвязанных колец одинаковой величины, каждое из которых является лентой Мебиуса;


- если ленту перекрутить трижды, то результат получится такой же, т.е. количество разрезов, совпадает с количеством колец одинаковой величины, каждое из которых является лентой Мебиуса, и вместе они образуют такую же поверхность;
Таким образом, лента Мёбиуса обладает не только свойством односторонности, но и такими неожиданными свойствами, как непрерывность и связность.
Глава 3. Применение листа Мёбиуса.
Мёбиуса лента понравилась не только математикам, но и фокусникам
Более 100 лет лист Мёбиуса используется для показа различных фокусов и развлечений. Удивительные свойства листа демонстрировались даже в цирке, где подвешивались яркие ленты, склеенные в виде листов Мёбиуса. Фокусник закуривал сигарету и горящим концом дотрагивался до средней линии каждой ленты, которая была выполнена из калийной селитры. Огненная дорожка превращала первую ленту в более длинную, а вторую - в две ленты, продетая одна в другую. (В этом случае фокусник разрезал лист Мёбиуса не посередине, а на расстоянии в одну треть его ширины).
О ленте Мёбиуса упоминается в художественной литературе.
Например, вот сюжет рассказа А.Дейча “Лента Мёбиуса”.
В одном городе находился огромных размеров метрополитен (или подземка, как называют метро в некоторых странах).
И вот однажды случилось так, что пути метрополитена пересеклись, и весь он стал напоминать огромную ленту Мёбиуса. И знаете, что стало происходить?
Поезда один за другим начали исчезать, появляясь снова только через несколько месяцев!
Поняли, почему? Потому что они как бы оказывались с внутренней стороны ленты! Вот она какая, эта лента Мёбиуса!..
Её не раз использовали художники и скульпторы. Довольно много разнообразных рисунков с изображением листа Мёбиуса оставил известный график М.Эшер (1898-1971). Особенно интересна гравюра с изображением муравья, ползающего по Ленте Мебиуса.
Серию вариантов листа Мёбиуса создал скульптор Макс Билл (родился в 1908). В течение почти 20 лет он неоднократно обращался к листу Мёбиуса, стремясь выразить в скульптуре идею вечного движения и развёртывающейся в пространстве формы. Скульптура «Узел без конца» находится в музее современного искусства в Париже.
Знания о листе Мёбиуса имеют и практическое значение в жизни человека.
Патентная служба зарегистрировала немало изобретений, в основе, которых лежит всё та же односторонняя поверхность. В 1923 году выдан патент изобретателю Ли де форсу, который предложил записывать звук на киноленте без смены катушек, сразу с двух сторон. Придуманы кассеты для магнитофона, где лента перекручивается и склеивается в кольцо, при этом появляется возможность записывать или считывать информацию сразу с двух сторон, что увеличивает ёмкость кассеты и соответственно время звучания.
В 1969 году советский изобретатель Губайдуллин предложил бесконечную шлифовальную ленту в виде листа Мёбиуса. В 1971 году изобретатель с Урала Чесноков П.Н. применил фильтр в виде листа Мёбиуса. Свойство односторонности ленты Мёбиуса используют в технике: если в ременной передаче ремень сделать в виде листа Мёбиуса, то его поверхность будет изнашиваться вдвое медленнее, чем у обычного кольца. Это даёт ощутимую экономию. Нами эти знания могут быть использованы на уроках технологии в швейных машинах.
Есть гипотеза, что спираль ДНК сама по себе тоже является фрагментом ленты Мебиуса и только поэтому генетический код так сложен для расшифровки и восприятия. Больше того - такая структура вполне логично объясняет причину наступления биологической смерти - спираль замыкается сама на себя и происходит самоуничтожение
ЗАКЛЮЧЕНИЕ
«Мышление начинается с удивления»,- заметил 2500 лет назад Аристотель. Наш современник Сухомлинский считал «что чувство удивления – могучий источник желания знать: от удивления к знаниям – один шаг». А математика замечательный предмет для удивления.
Именно это мы попытались показать в своей работе, описывая лист Мёбиуса и процесс его изготовления, раскрывая опытным путём свойства этого поразительного открытия. Наше предположение подтвердилось: лента Мёбиуса обладает не только свойством односторонности, но и такими, действительно, неожиданными свойствами, как непрерывность и связность. Лист Мёбиуса - первая односторонняя поверхность, которую открыл учёный. Позже математики открыли ещё целый ряд односторонних поверхностей. Но эта - самая первая, положившая начало целому направлению в геометрии, по - прежнему привлекает к себе внимание учёных, изобретателей, художников.
Представленная в работе односторонняя поверхность увековечена в памяти людей. У входа в Музей истории и техники в Вашингтоне медленно вращается на пьедестале стальная лента – лист Мёбиуса.
А в 1967г, когда в Бразилии состоялся международный математический конгресс, его устроители выпустили марку с изображением листа или ленты Мёбиуса.
В этой работе я пыталась описать свойства этой прекрасной поверхности-листа Мебиуса, показать его значимость на практике, доказать, что лист Мёбиуса - топологическая фигура.
Список литературы:
1. Воронец А.М. Математические развлечения. М. Учпедгиз, 1981
2. Гарднер М. Математические досуги. М. 1992
3. Кордемский Б.А. Топологические опыты своими руками./ «Квант» №3, 1974,стр73.
4. Коробенок Е.В., Столяр А.А. Сколько сторон у поверхности?: Беседы с учащимися VII-X классов. Минск: Народная асвета, 1995.
-
Леман И. Увлекательнаяматематика.М.Знание,1985
-
Материалы сайтов:
-
http://arbuz.uz/t_lenta.html
-
http://www.frei.ru/golos/books/
-
http://umiranie.chat.ru/sphere.htm
-
http://school-sector.relarn.ru/dckt/projects/ctrana/matric/t_lm1.htm
-
http://www.kvant.info/
-
http://www.websib.ru/noos/math/listmebiusa/
12





































