Россия, г. Касимов
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 03.06.2024 17:15
Барышникова Елена Михайловна
учитель математики
55 лет
1 674
30 790 
Местоположение
Специализация
Презентация на тему "Логарифмические неравенства, их типы и методы решения"
Категория:
Математика
13.06.2020 23:04
Просмотр содержимого документа
«Презентация на тему "Логарифмические неравенства, их типы и методы решения"»
Презентация на тему:
«Логарифмические неравенства, их типы и методы решения ».
Выполнила: учитель высшей квалификационной категории
Барышникова Е.М.
г. Касимов, 2020 г.
0, a ≠ 1) и прямой y = b y = log a x ( 0 y = log a x (a 1 ) y y y=b, b0 х 0 y=b, b = 0 х 0 x х 0 0 1 y=b, b0 y=b, b х 0 y=b, b = 0 x х 0 0 1 y=b, b " width="640"
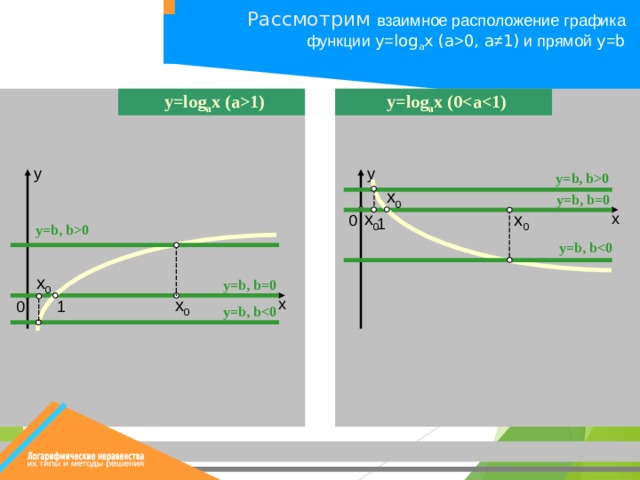
Рассмотрим взаимное расположение графика
функции y = log a x (a 0, a ≠ 1) и прямой y = b
y = log a x ( 0
y = log a x (a 1 )
y
y
y=b, b0
х 0
y=b, b = 0
х 0
x
х 0
0
1
y=b, b0
y=b, b
х 0
y=b, b = 0
x
х 0
0
1
y=b, b
0, a ≠ 1) и прямая y = b пересекаются в единственной точке, абсцисса которой x 0 = a b . " width="640"
ВЫВОД:
График функции y = log a x (a 0, a ≠ 1) и прямая y = b пересекаются в единственной точке, абсцисса которой x 0 = a b .
b (log a x ≥ b ) или log a x " width="640"
ОПРЕДЕЛЕНИЕ:
Пусть , тогда неравенства log a x b (log a x ≥ b ) или log a x
Что значит решить неравенство?
Решить неравенство - значит, найти все его решения или показать, что их нет.
Что называется решением неравенства?
Решением неравенства с неизвестным х называют число х 0 , при подстановке которого в неравенство вместо х получается верное числовое неравенство.
1 ) y Если для каждого соответствующая точка графика функции находится выше прямой y=b х 2 х 1 1 х 0 x 0 для каждого соответствующая точка графика функции находится ниже прямой " width="640"
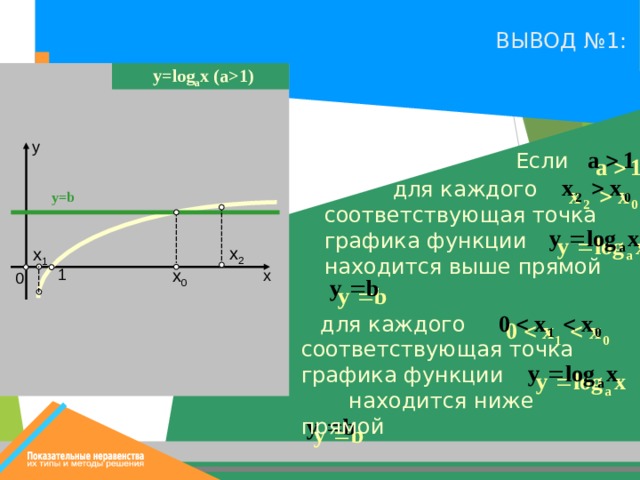
ВЫВОД №1:
y = log a x (a 1 )
y
Если
для каждого соответствующая точка графика функции находится выше прямой
y=b
х 2
х 1
1
х 0
x
0
для каждого
соответствующая точка графика функции находится ниже прямой
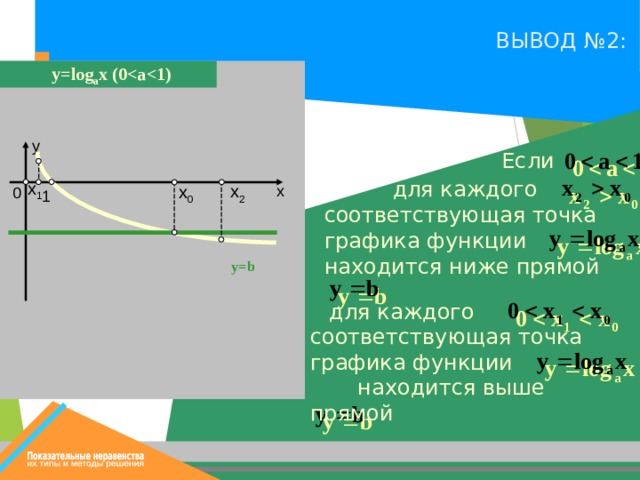
ВЫВОД №2:
y = log a x ( 0
y
Если
для каждого соответствующая точка графика функции находится ниже прямой
х 1
х 2
x
х 0
0
1
y=b
для каждого
соответствующая точка графика функции находится выше прямой
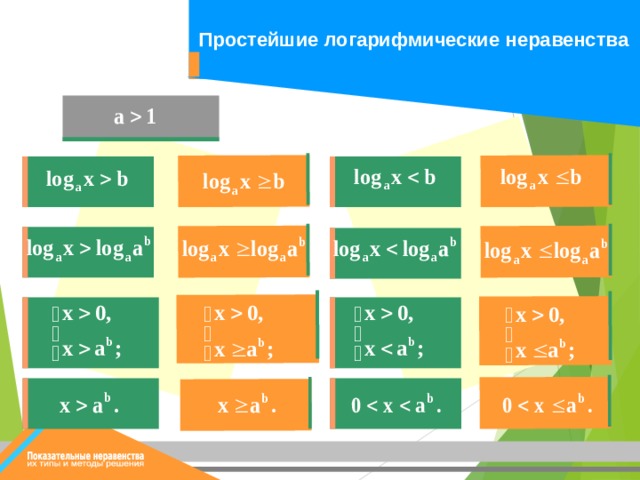
Простейшие логарифмические неравенства
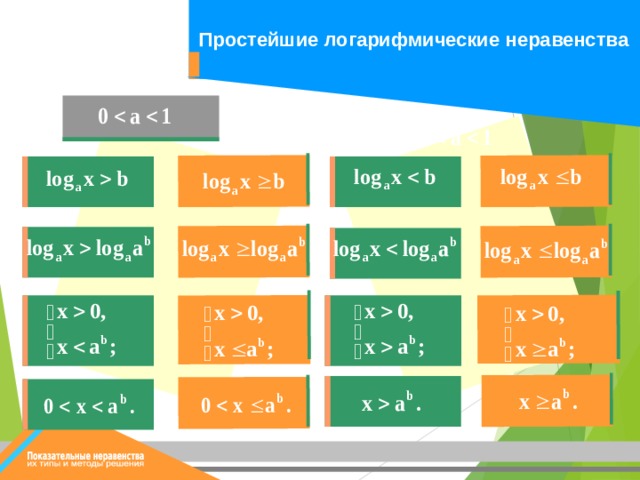
Простейшие логарифмические неравенства
Типы и методы решения логарифмических неравенств
1) Простейшие логарифмические неравенства
Пример №1
Решение:
убывает на всей
области определения и
то неравенство равносильно системе
Ответ:
(0,2; 0,4)
Типы и методы решения логарифмических неравенств
1) Простейшие логарифмические неравенства
Пример №2
Решение:
убывает
на всей области определения, то неравенство равносильно системе
Ответ:
(0,75; 2)
Типы и методы решения логарифмических неравенств
2) Логарифмические неравенства, сводящиеся к простейшим логарифмическим неравенствам
Решение:
Пример №1
возрастает на всей области
определения, то неравенство равносильно системе
то система равносильна неравенству
Ответ:
Типы и методы решения логарифмических неравенств
2) Логарифмические неравенства, сводящиеся к простейшим логарифмическим неравенствам
Решение:
Пример №2
возрастает на всей
области определения и
то неравенство равносильно системе
Ответ:
Типы и методы решения логарифмических неравенств
2) Логарифмические неравенства, сводящиеся к простейшим логарифмическим неравенствам
Решение:
Пример №3
убывает на всей области определения и
то неравенство равносильно системе
Ответ:
Типы и методы решения логарифмических неравенств
2) Логарифмические неравенства, сводящиеся к простейшим логарифмическим неравенствам
Решение:
Пример №4
возрастает на всей области определения и
то неравенство равносильно системе
Ответ:
Типы и методы решения логарифмических неравенств
3) Логарифмические неравенства, сводящиеся к неравенствам второй степени
Решение:
Пример №1
Вернёмся к переменной х
возрастает на всей области определения, то
Ответ:
Типы и методы решения логарифмических неравенств
3) Логарифмические неравенства, сводящиеся к неравенствам второй степени
Решение:
Пример №2
то для нахождения области допустимых значений
переменной х составим систему:
В найденной области допустимых значений переменной х преобразуем неравенство.
а также
возрастает на всей области определения и
С учётом области допустимых значений переменной х получим:
Ответ:
Типы и методы решения логарифмических неравенств
4) Логарифмические неравенства, сводящиеся к рациональным неравенствам
Решение:
Пример №1
Вернёмся к переменной х
возрастает на всей
области определения
Ответ:
Типы и методы решения логарифмических неравенств
4) Логарифмические неравенства, сводящиеся к рациональным неравенствам
Решение:
Пример №2
В найденной области допустимых
значений переменной х преобразуем
данное неравенство к виду:
Вернёмся к переменной х .
возрастает на
всей области определения и
Ответ:
Типы и методы решения логарифмических неравенств
5) Логарифмические неравенства с переменной в основании и под знаком логарифма
Решение:
Пример №1
Ответ:
Типы и методы решения логарифмических неравенств
5) Логарифмические неравенства с переменной в основании и под знаком логарифма
Решение:
Пример №2
Ответ:
Типы и методы решения логарифмических неравенств
5) Логарифмические неравенства с переменной в основании и под знаком логарифма
Решение:
Пример №3
Ответ:
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
Полезное для учителя
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
