Дисциплина: математика
Тема: «Решение простейших и сводящихся к ним
логарифмических уравнений и неравенств»
Цели и задачи занятия:
Дидактическая:
- повторение теоретического материала,
- закрепление умения применять свойства при решении логарифмических уравнений и неравенств,
- обобщение приобретенных знаний.
Развивающая:
- развитие логического мышления, речи, вычислительных навыков и навыков самостоятельной работы,
- формирование умения обобщать, систематизировать.
Воспитательная:
- воспитание умения слушать,
- воспитание воли и настойчивости для достижения конечных результатов при решении логарифмических уравнений и неравеств,
- воспитание интереса к математике, расширение кругозора.
Методическая: применение информационных и коммуникационных технологии.
Тип урока: урок проверки знаний, умений и навыков.
Форма проведения: урок - соревнование.
Методы обучения: словесный, наглядно-иллюстративный; частично- поисковый; методы контроля и самоконтроля.
Межпредметные связи: история, литература.
Средства обучения: интерактивная доска (презентации и флипчарты), карточки с заданиями, оценочная таблица, призы для всех участников.
Просмотр содержимого документа
«Решение логарифмических уравнений и неравенств»
План
проведения открытого занятия
Дата:
Время:
Место проведения:
Преподаватель:
Группа:
Дисциплина: математика
Тема: «Решение простейших и сводящихся к ним
логарифмических уравнений и неравенств»
Цели и задачи занятия:
Дидактическая:
повторение теоретического материала,
закрепление умения применять свойства при решении логарифмических уравнений и неравенств,
обобщение приобретенных знаний.
Развивающая:
развитие логического мышления, речи, вычислительных навыков и навыков самостоятельной работы,
формирование умения обобщать, систематизировать.
Воспитательная:
воспитание умения слушать,
воспитание воли и настойчивости для достижения конечных результатов при решении логарифмических уравнений и неравеств,
воспитание интереса к математике, расширение кругозора.
Методическая: применение информационных и коммуникационных технологии.
Тип урока: урок проверки знаний, умений и навыков.
Форма проведения: урок - соревнование.
Методы обучения: словесный, наглядно-иллюстративный; частично- поисковый; методы контроля и самоконтроля.
Межпредметные связи: история, литература.
Средства обучения: интерактивная доска (презентации и флипчарты), карточки с заданиями, оценочная таблица, призы для всех участников.
Структурно-логическая схема
и хронологическая карта занятия:
Организационный момент - 2 мин
Приветствие, проверка готовности к занятию.
Сообщение темы, цели и задач занятия.
Проверка знаний, умений и навыков –45 мин
Проверка теоретического материала - «Математический диктант»
Проверка практической части материала – «Морской бой».
Историческая справка о возникновении логарифмов.
Решение логарифмических уравнений и неравенств.
Домашнее задание – 3 мин
Подведение итогов занятия - 5 мин
Анализ работы обучающихся.
Выставление и комментирование оценок.
Рефлексия - 5 мин
Ход урока.
Организационный момент
Приветствие, проверка готовности к занятию.
Сообщение темы, цели и задач занятия – повторение теоретического материала, закрепление умения применять свойства при решении логарифмических уравнений и неравенств в ходе соревнования 3х команд.
Представление команд – названия команд и капитанов.
Проверка и коррекция знаний, умений и навыков
Проверка теоретического материала – «Математический диктант», Вопросы – задания, на которые обучающийся отвечает «да» или «нет».
Ответы вывешиваются на доске. Проверяют обучающийся работу соседа (работа в паре). Да(+); Нет(-)
1. Логарифмическая функция 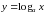 определена при любом х.
определена при любом х.
2. Функция 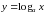 логарифмическая при
логарифмическая при 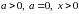 .
.
3. Область определения логарифмической функции является множество действительных чисел.
4. Область значений логарифмической функции является множество действительных чисел.
5. Логарифмическая функция – четная.
6. Логарифмическая функция – нечетная.
7. Функция 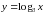 – возрастающая.
– возрастающая.
8. Функция 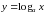 при
при 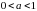 – возрастающая.
– возрастающая.
9. Логарифмическая функция имеет экстремум в точке (1;0).
10. График функции 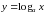 пересекается с осью Ох.
пересекается с осью Ох.
11. График логарифмической функции находится в верхней полуплоскости.
12. График логарифмической функции симметричен относительно Ох.
13. График логарифмической функции всегда находится в I и IV четвертях.
14. График логарифмической функции всегда пересекает Ох в точке (1;0).
15. Существует логарифм отрицательного числа.
16. Существует логарифм дробного положительного числа.
17. График логарифмической функции проходит через точку (0;0).
Проверка практической части материала – «Морской бой»
В некоторых ячейках есть буквы . После решения всех заданий из этих букв выстраивается фамилия математика, изобретателя логарифма.
Историческая справка о Джоне Непере, и о возникновении логарифмов (сообщение обучающегося).
В качестве опережающего  домашнего задания предложено подготовить сообщение о Джоне Непере, который одним из первых преобрел систему логарифмов.
домашнего задания предложено подготовить сообщение о Джоне Непере, который одним из первых преобрел систему логарифмов.
Решение логарифмических уравнений и неравенств
Какие методы решения логарифмических уравнений существуют : 1. метод решения с помощью определения; 2. метод потенцирования; 3. метод введения вспомогательной переменной.
На доске заданы разноуровневые примеры. С каждой команды обучающийся выбирает любое задание и решает у доски.
Домашнее задание: № 518(в,г), № 517(в,г),№525(в,г)
Подведение итгов занятия
Анализ работы обучающихся.
Выставление и комментирование оценок
Рефлексия






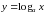 определена при любом х.
определена при любом х. 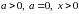 .
.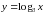 – возрастающая.
– возрастающая.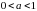 – возрастающая.
– возрастающая.
 домашнего задания предложено подготовить сообщение о Джоне Непере, который одним из первых преобрел систему логарифмов.
домашнего задания предложено подготовить сообщение о Джоне Непере, который одним из первых преобрел систему логарифмов.









