
Тема урока Логарифмы

Цель урока:
Разобрать понятие
логарифма числа
и его свойства.

Джон Непер - изобретатель системы
логарифмов, основанной на установ- лении соответствия между арифмети- ческой и геометрической числовыми прогрессиями.
В «Описании удивительной таблицы
логарифмов» он опубликовал первую
таблицу логарифмов (ему же принадлежит и сам термин «логарифм»). Объяснение таблицы было дано в его сочинении «Построение удивительной
таблицы логарифмов», вышедшем в 1619. Таблицы логарифмов, насущно необходимые астрономам, нашли немедленное применение.
Джон Непер
(1550-1617)
 0, а ≠1, называется показатель степени , в которую надо возвести число а , чтобы получить b . log a b= х " width="640"
0, а ≠1, называется показатель степени , в которую надо возвести число а , чтобы получить b . log a b= х " width="640"
Определение логарифма
Логарифмом положительного числа b
по основанию а , где а 0, а ≠1,
называется показатель степени ,
в которую надо возвести число а ,
чтобы получить b .
log a b= х
 0, а 0, а ≠1. " width="640"
0, а 0, а ≠1. " width="640"
Основное логарифмическое тождество
a log a b = b
b 0, а 0, а ≠1.

Определение логарифма
Из определения логарифма следует, что нахождение
log a b = x
равносильно решению уравнения
a x = b .
Например:
log 2 8 = 3 , потому что 2 3 = 8 .

Логарифмирование
Логарифмированием называют действие
нахождения логарифма числа .
Читается: логарифм b по основанию a .
Прочитайте
так как 5 2 =25
log 5 25 = 2,
так как 4 -2 =1 /16
log 4 (1 / 16) = -2,
так как (1/3) - 3 = 27
log 1/3 27 = -3 ,

Примеры

Примеры

Найдите значения выражения
3
log 5 625=
log 3 27=
4
-2
log 0,5 4=
log 10 0,001=
-3
log 11 1=
0
log 3 81=
4
Еще пример
Найти x
По определению логарифма
Так как
то
Откуда

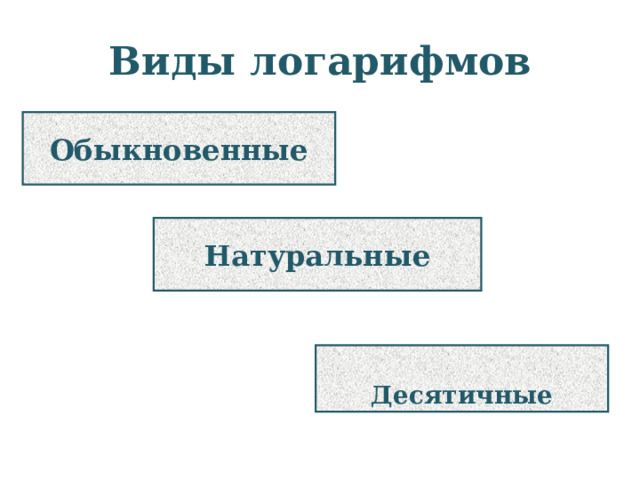
Виды логарифмов
Обыкновенные
Натуральные
Десятичные

Обыкновенные логарифмы :
Читается: «логарифм 7 по основанию 2»

Натуральные логарифмы :
Читается: «натуральный логарифм 5»

Десятичные логарифмы :
Читается: «десятичный логарифм 3»

Основные свойства логарифмов
 0, a=1, c0. Тогда " width="640"
0, a=1, c0. Тогда " width="640"
Логарифм произведения
Логарифм произведения положительных
чисел равен сумме логарифмов множителей
Пусть а 0, a=1, c0. Тогда

Логарифм произведения
пример
log 6 2 + log 6 3= log 6 ( 2 ∙ 3 ) = log 6 6=1
 0, a=1, c0. Тогда " width="640"
0, a=1, c0. Тогда " width="640"
Логарифм частного
Логарифм частного двух положительных
чисел равен разности логарифмов делимого
и делителя
Пусть а 0, a=1, c0. Тогда

Логарифм частного
пример

Самостоятельно

проверка
 0, b0. r – любое действительное число. Тогда " width="640"
0, b0. r – любое действительное число. Тогда " width="640"
Логарифм степени
Логарифм степени с положительным
основанием равен показателю степени,
умноженному на логарифм основания
степени
Пусть а 0, b0. r – любое действительное
число. Тогда

пример
Логарифм степени
 0, a≠1, b0, c0, c ≠1 " width="640"
0, a≠1, b0, c0, c ≠1 " width="640"
Переход к новому основанию
Для перехода от логарифма по одному
основанию к логарифму по другому
основанию используется формула:
где a0, a≠1, b0, c0, c ≠1

Переход к новому основанию
пример

самостоятельно

проверка
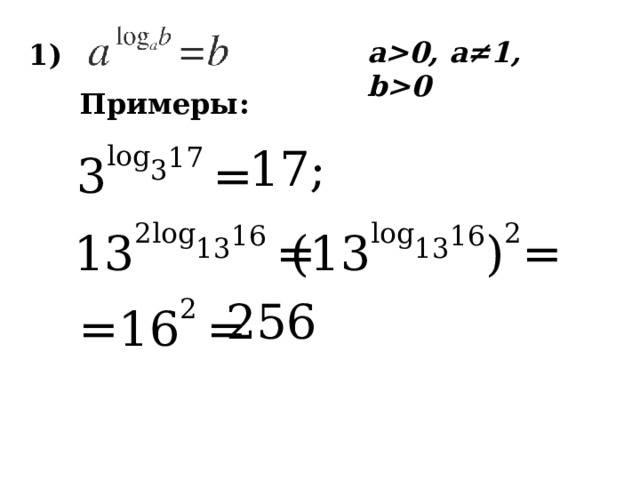
Свойства логарифмов
 0, a≠1, b0 1) Примеры: 3 log 3 17 = 17 ; 13 2 log 13 16 = (1 3 log 13 16 ) 2 = =16 2 = 256 " width="640"
0, a≠1, b0 1) Примеры: 3 log 3 17 = 17 ; 13 2 log 13 16 = (1 3 log 13 16 ) 2 = =16 2 = 256 " width="640"
a0, a≠1, b0
1)
Примеры:
3 log 3 17 =
17 ;
13 2 log 13 16 =
(1 3 log 13 16 ) 2 =
=16 2 =
256
 0, a≠1 2 ) Пример: 1 0 3 ) a0, a≠1 Пример: 0 " width="640"
0, a≠1 2 ) Пример: 1 0 3 ) a0, a≠1 Пример: 0 " width="640"
1
a0, a≠1
2 )
Пример:
1
0
3 )
a0, a≠1
Пример:
0
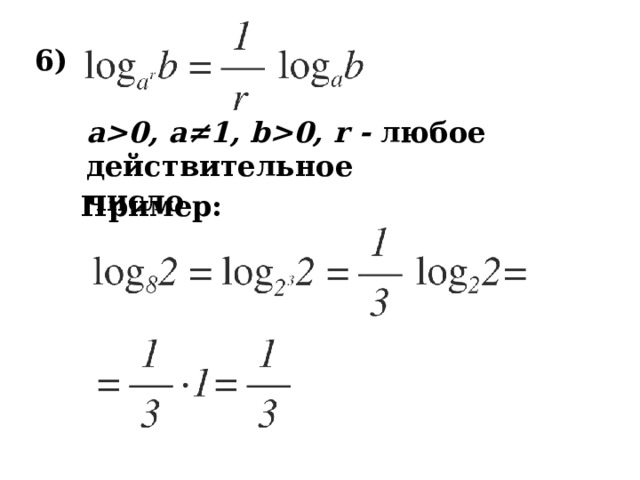 0, a≠1, b0, r- любое действительное число Пример: 5 ) a0, a≠1, b0 Пример: " width="640"
0, a≠1, b0, r- любое действительное число Пример: 5 ) a0, a≠1, b0 Пример: " width="640"
4 )
a0, a≠1, b0, r- любое действительное число
Пример:
5 )
a0, a≠1, b0
Пример:
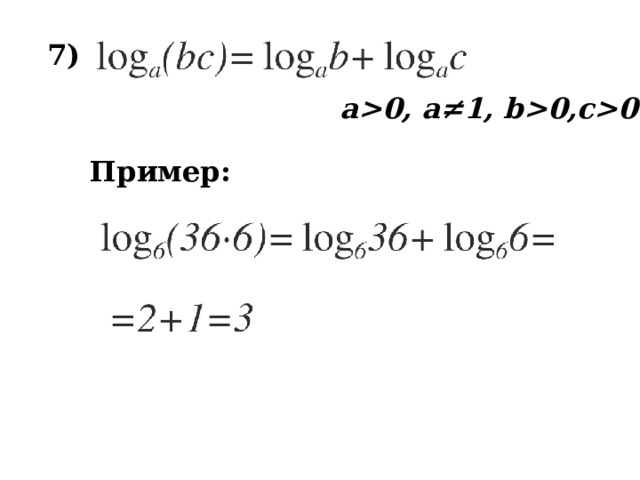 0, a≠1, b0, r - любое действительное число Пример: " width="640"
0, a≠1, b0, r - любое действительное число Пример: " width="640"
6 )
a0, a≠1, b0, r - любое действительное
число
Пример:
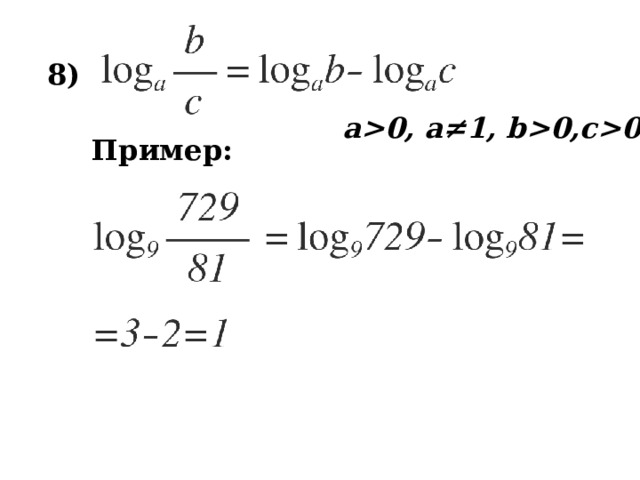 0, a≠1, b0,c0 Пример: " width="640"
0, a≠1, b0,c0 Пример: " width="640"
7 )
a0, a≠1, b0,c0
Пример:
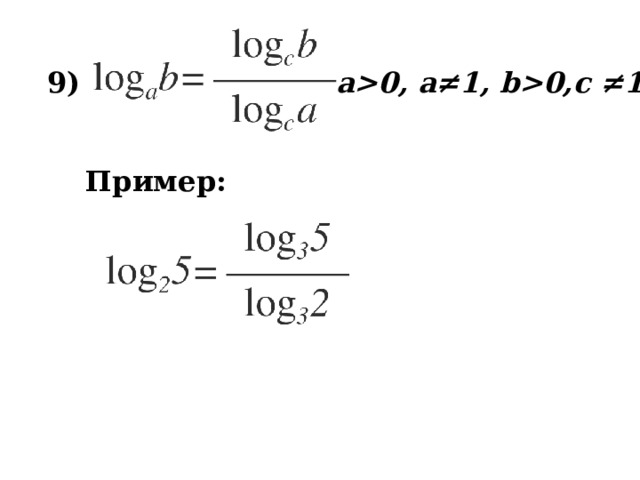 0, a≠1, b0,c0 Пример: " width="640"
0, a≠1, b0,c0 Пример: " width="640"
8 )
a0, a≠1, b0,c0
Пример:
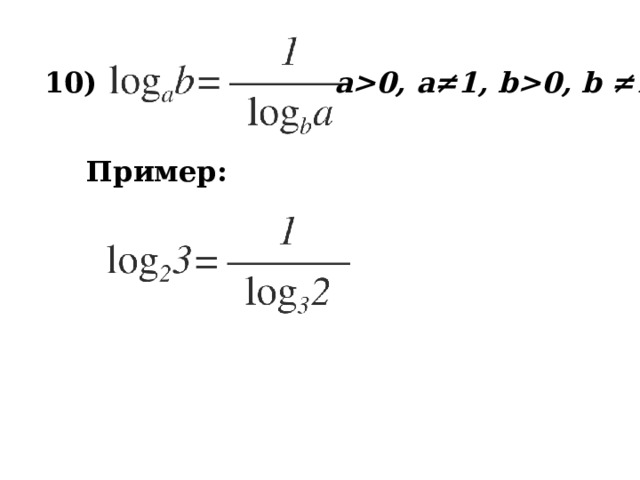 0, a≠1, b0,c ≠1 Пример: " width="640"
0, a≠1, b0,c ≠1 Пример: " width="640"
9 )
a0, a≠1, b0,c ≠1
Пример:
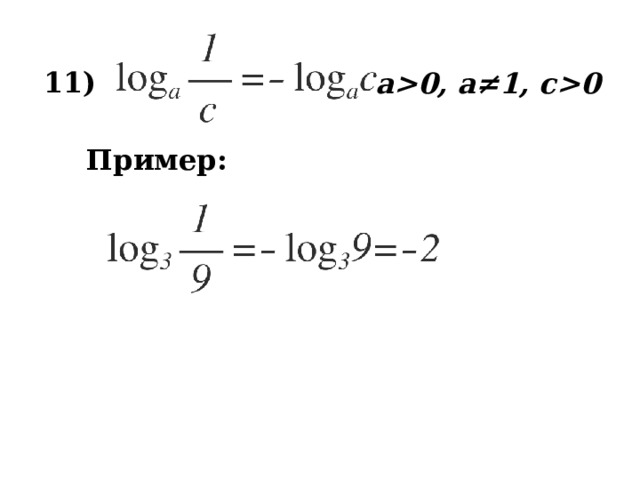 0, a≠1, b0, b ≠1 Пример: " width="640"
0, a≠1, b0, b ≠1 Пример: " width="640"
10 )
a0, a≠1, b0, b ≠1
Пример:
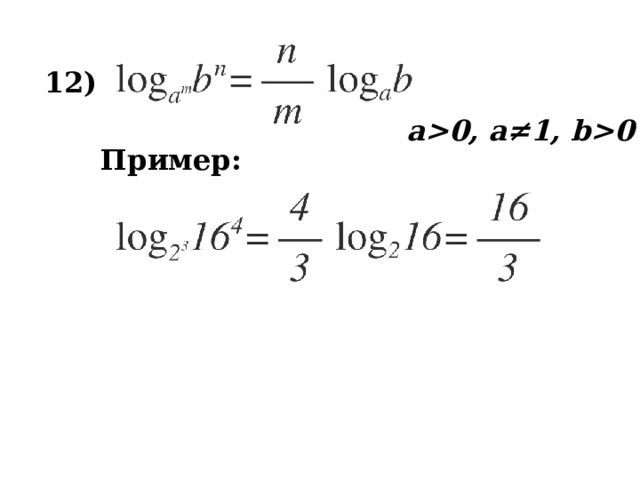 0, a≠1, c0 Пример: " width="640"
0, a≠1, c0 Пример: " width="640"
11 )
a0, a≠1, c0
Пример:
 0, a≠1, b0 Пример: " width="640"
0, a≠1, b0 Пример: " width="640"
12 )
a0, a≠1, b0
Пример:
 0, c≠1, b0,c0 Пример: " width="640"
0, c≠1, b0,c0 Пример: " width="640"
13 )
a0, c≠1, b0,c0
Пример:

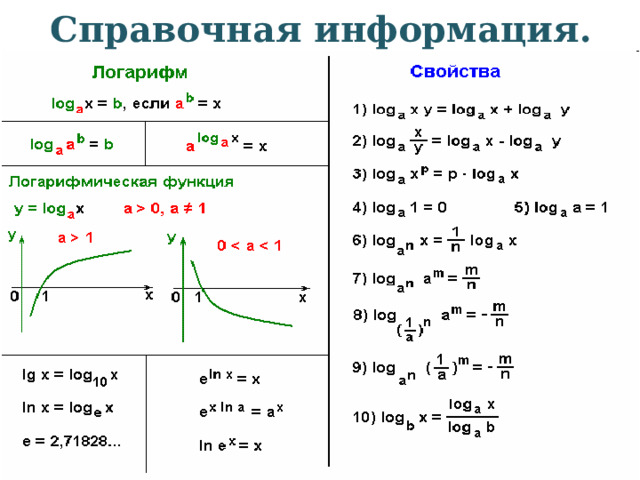
Справочная информация.

Закончите предложение
- Сегодня на уроке я узнал ….
- Сегодня на уроке мне было интересно…

Спасибо за внимание










 0, а ≠1, называется показатель степени , в которую надо возвести число а , чтобы получить b . log a b= х " width="640"
0, а ≠1, называется показатель степени , в которую надо возвести число а , чтобы получить b . log a b= х " width="640"
 0, а 0, а ≠1. " width="640"
0, а 0, а ≠1. " width="640"











 0, a=1, c0. Тогда " width="640"
0, a=1, c0. Тогда " width="640"

 0, a=1, c0. Тогда " width="640"
0, a=1, c0. Тогда " width="640"



 0, b0. r – любое действительное число. Тогда " width="640"
0, b0. r – любое действительное число. Тогда " width="640"

 0, a≠1, b0, c0, c ≠1 " width="640"
0, a≠1, b0, c0, c ≠1 " width="640"



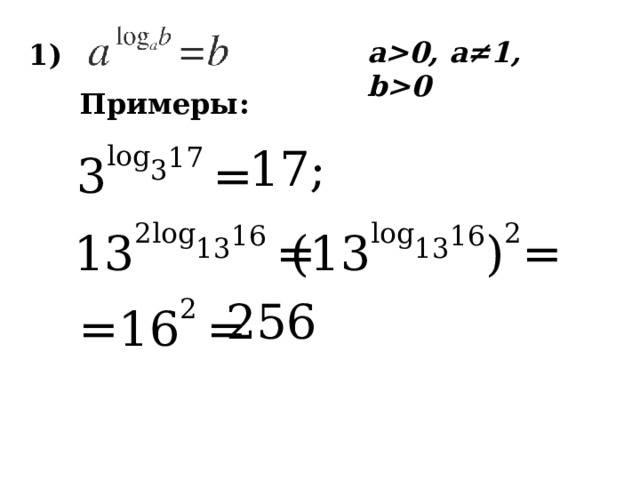
 0, a≠1, b0 1) Примеры: 3 log 3 17 = 17 ; 13 2 log 13 16 = (1 3 log 13 16 ) 2 = =16 2 = 256 " width="640"
0, a≠1, b0 1) Примеры: 3 log 3 17 = 17 ; 13 2 log 13 16 = (1 3 log 13 16 ) 2 = =16 2 = 256 " width="640"
 0, a≠1 2 ) Пример: 1 0 3 ) a0, a≠1 Пример: 0 " width="640"
0, a≠1 2 ) Пример: 1 0 3 ) a0, a≠1 Пример: 0 " width="640"
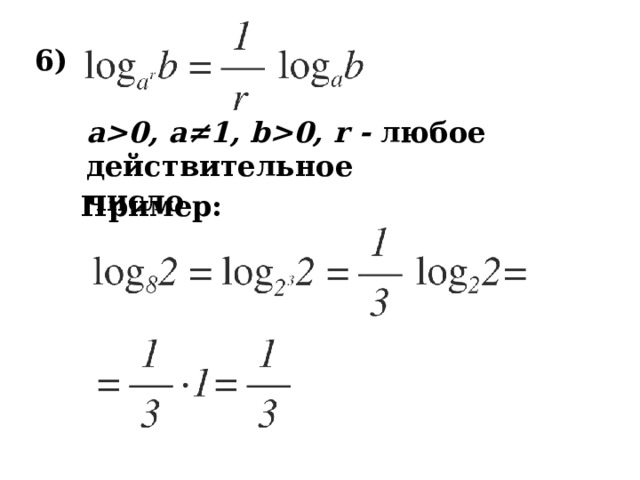 0, a≠1, b0, r- любое действительное число Пример: 5 ) a0, a≠1, b0 Пример: " width="640"
0, a≠1, b0, r- любое действительное число Пример: 5 ) a0, a≠1, b0 Пример: " width="640"
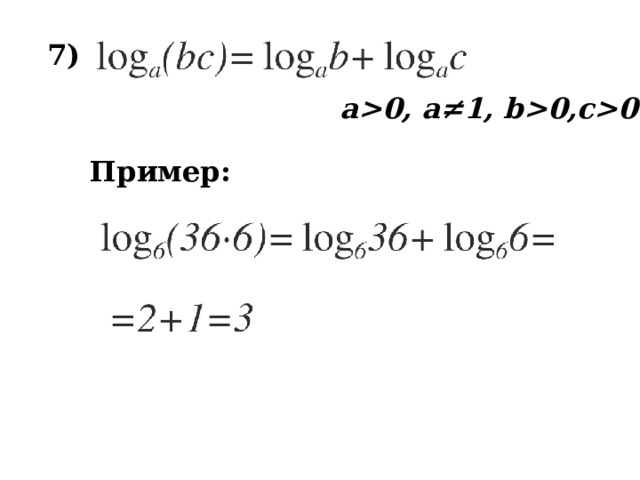 0, a≠1, b0, r - любое действительное число Пример: " width="640"
0, a≠1, b0, r - любое действительное число Пример: " width="640"
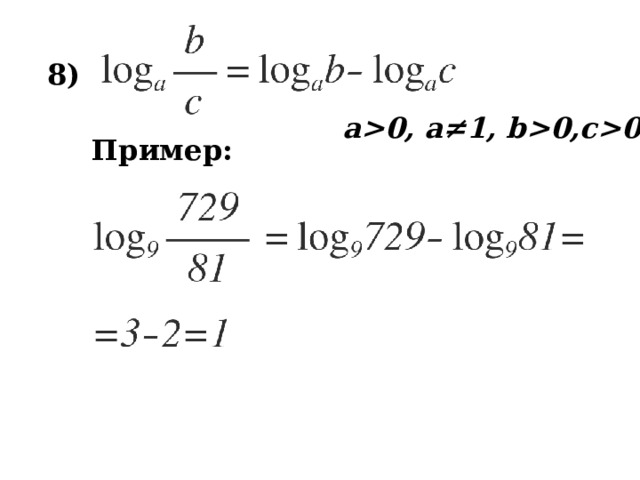 0, a≠1, b0,c0 Пример: " width="640"
0, a≠1, b0,c0 Пример: " width="640"
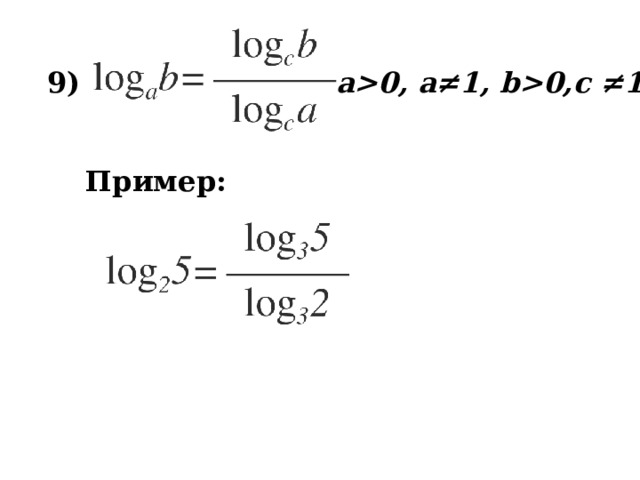 0, a≠1, b0,c0 Пример: " width="640"
0, a≠1, b0,c0 Пример: " width="640"
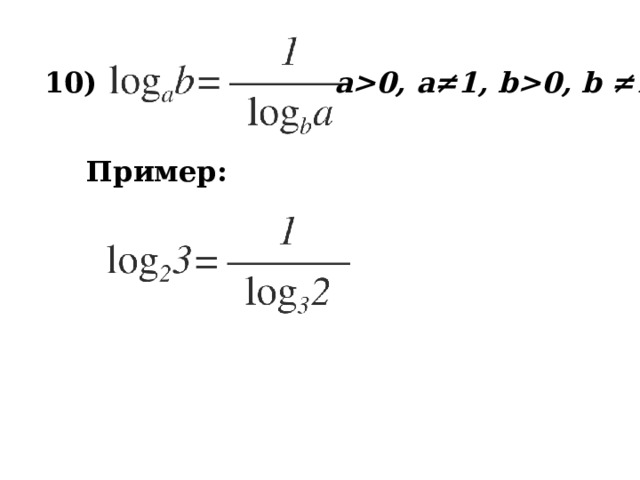 0, a≠1, b0,c ≠1 Пример: " width="640"
0, a≠1, b0,c ≠1 Пример: " width="640"
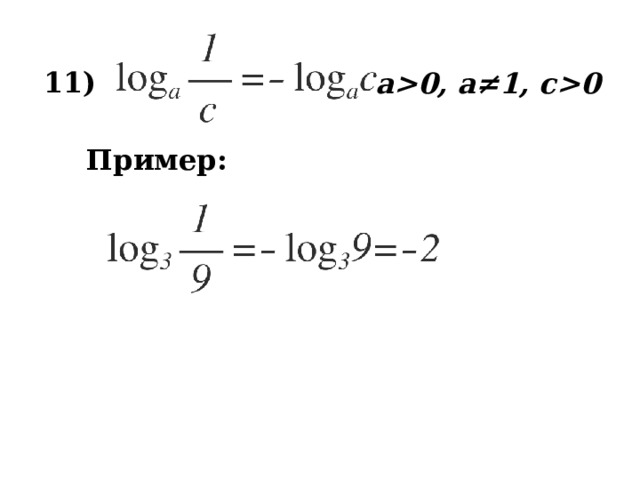 0, a≠1, b0, b ≠1 Пример: " width="640"
0, a≠1, b0, b ≠1 Пример: " width="640"
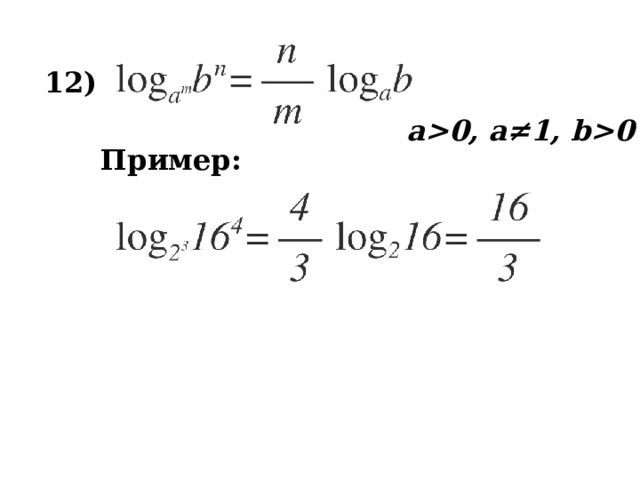 0, a≠1, c0 Пример: " width="640"
0, a≠1, c0 Пример: " width="640"
 0, a≠1, b0 Пример: " width="640"
0, a≠1, b0 Пример: " width="640"
 0, c≠1, b0,c0 Пример: " width="640"
0, c≠1, b0,c0 Пример: " width="640"






















