Просмотр содержимого документа
«Логарифмы (Решение упражнений)»
Решение упражнений (логарифмы)
- Запишите тему занятия.
- Решите в тетради задания из учебника «Проверь себя!» (с. 112), №2 не решайте. (Если будете списывать, разберитесь в решениях, т.к. подобные задания будут на контрольной работе и на экзамене).
И решайте полные квадратные уравнения через дискриминант! Не надо раскладывать на множители! Если вы раскладываете на множители или решаете по теореме Виета, то выучите эти методы – я проверю, иначе снижаю оценки!
Примеры:
Вычислить (1 – 3)
1.  .
.
2. 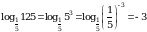 .
.
3.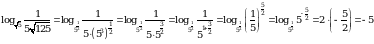 .
.
Обратите внимание, в примере 3 мы использовали формулы:
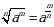 ;
;
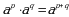 ;
;
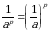 ;
;
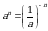 ;
;
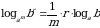 ;
;
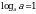 .
.
Сравнить, используя свойства логарифмов (4, 5):
4. 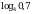 и
и 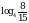 ;
;
Основание логарифма равно 4. 4 1, значит, функция возрастает, т.е. чем больше подлогарифмическое выражение, тем больше и значение логарифма.
1, значит, функция возрастает, т.е. чем больше подлогарифмическое выражение, тем больше и значение логарифма.
Сравним 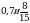
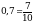 , приведем к общему знаменателю
, приведем к общему знаменателю 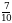 и
и 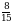 . Общим знаменателем может быть число 30, т.к. оно делится на оба знаменателя данных дробей 10 и 15.
. Общим знаменателем может быть число 30, т.к. оно делится на оба знаменателя данных дробей 10 и 15.
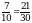 ;
; 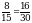 . Теперь сравним и получим, что
. Теперь сравним и получим, что 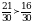 , т.е.
, т.е. 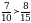 , следовательно,
, следовательно, 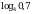

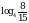
5. 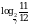 и
и 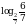 ;
;
Основание логарифма равно 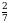 .
. 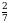
 1, значит, функция убывает, т.е. чем больше подлогарифмическая функция, тем меньше значение логарифма.
1, значит, функция убывает, т.е. чем больше подлогарифмическая функция, тем меньше значение логарифма.
Сравним 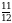 и
и 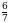 . Для этого приведем дроби к общему знаменателю. 12 и 7 не имеют общих делителей, поэтому общий знаменатель найдем, перемножив их, получим 84. Домножим числители дробей на недостающие множители, получим:
. Для этого приведем дроби к общему знаменателю. 12 и 7 не имеют общих делителей, поэтому общий знаменатель найдем, перемножив их, получим 84. Домножим числители дробей на недостающие множители, получим: 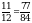 и
и 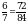 .
. 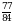

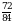 , т.е.
, т.е. 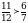 ,
,
следовательно, 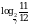

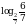 .
.
Вычислить (используем основное логарифмическое тождество: 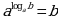 )
)
6. 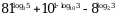 ;
;
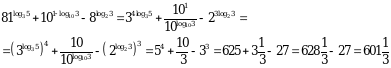
- Рассмотрите примеры и перепишите их в тетрадь. Пояснения, выделенные курсивом, переписывать не надо, это для того, чтобы вы поняли. Смотрите внимательно! Подчеркнутые пояснения в решение надо записывать обязательно.
- Как решаются логарифмические уравнения и неравенства, повторите по предыдущим занятиям.
- Решите упражнения:
1. Вычислить: а) 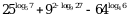 ; б)
; б) 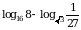 .
.
2. Сравнить: а) 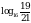 и
и 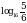 ; б)
; б) 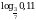 и
и 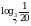 .
.
3. Решить уравнения: а) 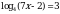 ; б)
; б) 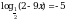 .
.
4. № 381, №383 – неравенства. Решать подробно, разбираясь в каждом шаге! И записывать подробно, буду проверять ОЧЕНЬ внимательно. И решайте полные квадратные уравнения через дискриминант! Не надо раскладывать на множители!
Работы прислать __________.






 .
.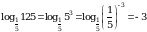 .
.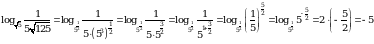 .
.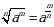 ;
; 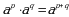 ;
; 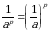 ;
; 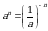 ;
; 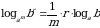 ;
; 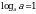 .
.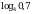 и
и 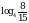 ;
; 1, значит, функция возрастает, т.е. чем больше подлогарифмическое выражение, тем больше и значение логарифма.
1, значит, функция возрастает, т.е. чем больше подлогарифмическое выражение, тем больше и значение логарифма.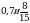
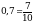 , приведем к общему знаменателю
, приведем к общему знаменателю 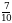 и
и 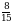 . Общим знаменателем может быть число 30, т.к. оно делится на оба знаменателя данных дробей 10 и 15.
. Общим знаменателем может быть число 30, т.к. оно делится на оба знаменателя данных дробей 10 и 15.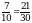 ;
; 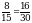 . Теперь сравним и получим, что
. Теперь сравним и получим, что 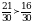 , т.е.
, т.е. 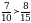 , следовательно,
, следовательно, 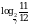 и
и 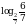 ;
;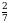 .
.  1, значит, функция убывает, т.е. чем больше подлогарифмическая функция, тем меньше значение логарифма.
1, значит, функция убывает, т.е. чем больше подлогарифмическая функция, тем меньше значение логарифма.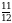 и
и 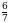 . Для этого приведем дроби к общему знаменателю. 12 и 7 не имеют общих делителей, поэтому общий знаменатель найдем, перемножив их, получим 84. Домножим числители дробей на недостающие множители, получим:
. Для этого приведем дроби к общему знаменателю. 12 и 7 не имеют общих делителей, поэтому общий знаменатель найдем, перемножив их, получим 84. Домножим числители дробей на недостающие множители, получим: 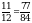 и
и 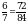 .
. 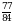
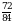 , т.е.
, т.е. 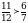 ,
, 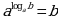 )
)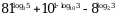 ;
;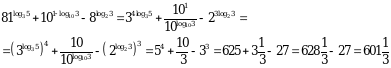
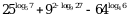 ; б)
; б) 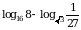 .
.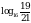 и
и 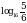 ; б)
; б) 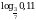 и
и 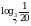 .
.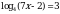 ; б)
; б) 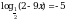 .
.









