Логические задачи. Алгоритмы и методы решения

Математика

ЛОГИЧЕСКИЕ ЗАДАЧИ. АЛГОРИТМЫ И МЕТОДЫ РЕШЕНИЯ

от древне-греческого λόγος — «рассуждение», «мысль», «разум»

ЛОГИКА

- это наука о законах, принципах и методах идеализированных рассуждений, выражающих результаты рациональной мыслительной деятельности человека, а также о языке как средстве такой деятельности.

Основы логики были заложены работами ученого и философа Аристотеля (384-322 гг. до н.э.). Он изучал правила мышления, впервые дал систематическое изложение логики.

ОСНОВОПОЛОЖНИКИ ЛОГИКИ

МЕТОДЫ РЕШЕНИЯ ЛОГИЧЕСКИХ ЗАДАЧ

• Метод рассуждений
• Метод Блок-схем
• Метод кругов Эйлера
• Метод Графов
• Метод решения задач с помощью полупрямой
• Метод математического бильярда
• Метод таблиц

МЕТОД РАССУЖДЕНИЙ

Этим способом обычно решают несложные логические задачи.

Его идея состоит в том, что мы проводим рассуждения, используя последовательно все условия задачи, и приходим к выводу, который и будет являться ответом задачи.

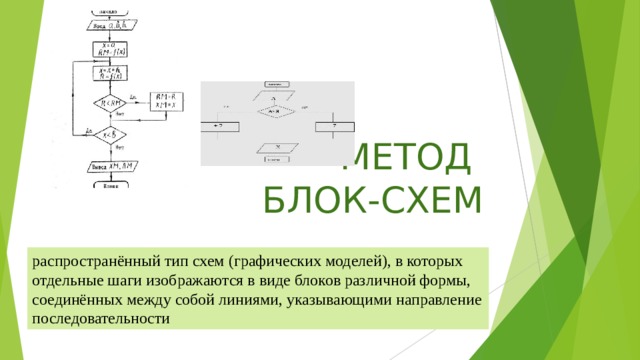
МЕТОД БЛОК-СХЕМ

распространённый тип схем (графических моделей), в которых отдельные шаги изображаются в виде блоков различной формы, соединённых между собой линиями, указывающими направление последовательности

МЕТОД К РУГ И ЭЙЛЕРА

Геометрическая схема, с помощью которой можно решать графически математические задачи на основе применения теории множеств.

Использование рисунка делает решение задачи простым и наглядным.

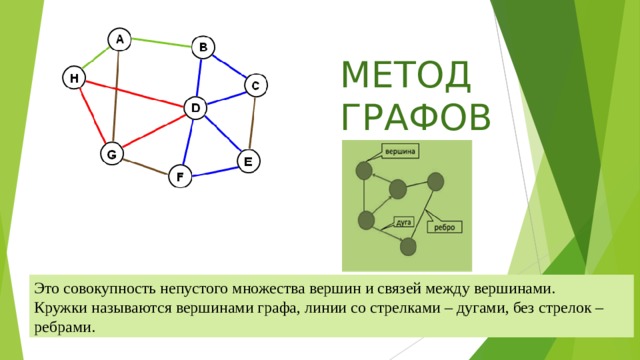
МЕТОД ГРАФОВ

Это совокупность непустого множества вершин и связей между вершинами.

Кружки называются вершинами графа, линии со стрелками – дугами, без стрелок – ребрами.

МЕТОД РЕШЕНИЯ ЗАДАЧ С ПОМОЩЬЮ ПОЛУПРЯМОЙ

Если в задаче имеется множество объектов и требуется установить взаимоотношение между элементами этого множества, то задачу можно решать на полупрямой.

МЕТОД МАТЕМАТИЧЕСКОГО БИЛЬЯРДА

Заключается в представлении последовательности переливаний аналогично движению бильярдного шарика по столу особой конструкции с размерами, соответствующими объемам первоначально пустых сосудов.

Необходимо проследить возможные движения шарика в соответствии с законом «угол падения равен углу отражения» и попадание им в требуемые точки по условию задачи.

МЕТОД ТАБЛИЦ

Используется при решении текстовых логических задач , заключается в построении таблиц.

Таблицы не только позволяют наглядно представить условие задачи или ее ответ, но в значительной степени помогают делать правильные логические выводы в ходе решения задачи

РЕКОМЕНДАЦИИ ДЛЯ РАЗВИТИЯ ЛОГИЧЕСКИХ СПОСОБНОСТЕЙ

• Играть в настольные стратегические игры, шахматы, домино, шашки, математические игры.

• Смотреть программы о науке и математике, научных открытиях. Читать научно-популярную литературу.

• Решать простые математические задачки в уме.

• Разгадывать головоломки.

• Анализировать цифры в новостях. Что они на самом деле означают?

• Изучать языки компьютерного программирования.