МАТЕМАТИЧЕСКИЕ МОДЕЛИ ДИНАМИЧЕСКИХ СИСТЕМ
Первоначально термин «динамическая система» применялся в основном к механическим системам, движение которых описывается дифференциальными уравнениями. Основные результаты о динамических системах были получены А.М. Ляпуновым и А. Пуанкаре в конце девятнадцатого века. Позднее стало очевидно, что понятие динамических систем полезно для анализа различных эволюционных процессов, изучаемых во многих науках. Определение динамической системы является математической формализацией общей научной концепции детерминированного процесса. Процесс называется детерминированным, если весь его будущий ход и все его прошлое однозначно определяются состоянием в настоящее время.
Будущее состояние многих физических, биологических, экологических и даже общественных систем может быть предсказано в некоторых пределах, если известно настоящее состояние и закон, управляющей их эволюцией.
Широкий круг явлений природы, а также многие технические объекты могут быть описаны дифференциальными уравнениями. Они являются естественным языком для описания разнообразных динамических систем, таких как движение планет Солнечной системы, процесс образования волн на море, функционирование атомных станций, систем автоматического управления космическими кораблями и т. д. Поэтому математические модели в виде дифференциальных уравнений играют важную роль в теории моделирования.
1. Классификация дифференциальных уравнений
Дифференциальные уравнения представляют собой соотношения, связывающие переменные и их производные. По количеству независимых переменных дифференциальные уравнения делятся на два больших класса: обыкновенные дифференциальные уравнения и дифференциальные уравнения с частными производными.
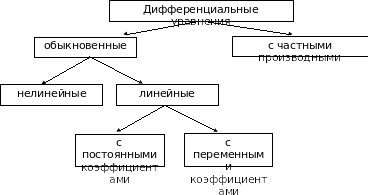
Рис. 1.1. Классификация дифференциальных уравнений
К первому классу относятся уравнения, в которых имеется только одна независимая переменная, например время. В уравнения второго класса входят несколько независимых переменных, например время и пространственные координаты. Как правило, решать эти уравнения значительно труднее.
Общая запись обыкновенного дифференциального уравнения имеет вид
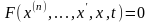 .
.
Наивысший порядок входящей в него производной называется порядком уравнения.
Дифференциальное уравнение называется линейным, если функция F линейна, и нелинейным – в противном случае. Простейшими примерами могут служить уравнения 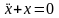 и
и 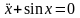 . Первое из них – линейное, оно приближенно описывает малые колебания математического маятника, второе (нелинейное) описывает колебания произвольной амплитуды.
. Первое из них – линейное, оно приближенно описывает малые колебания математического маятника, второе (нелинейное) описывает колебания произвольной амплитуды.
Если коэффициенты линейного дифференциального уравнения зависят от времени, то говорят о линейном уравнении с переменными коэффициентами. В тех случаях, когда коэффициенты постоянные, уравнение называется стационарным, или уравнением с постоянными коэффициентами. Классификация дифференциальных уравнений по перечисленным признакам приведена на рис. 1.1.
Для линейных дифференциальных уравнений разработаны аналитические методы их решения. теория нелинейных дифференциальных уравнений развита значительно хуже. общих методов решения таких уравнений не существует, описаны лишь отдельные типы уравнений, которые могут быть проинтегрированы, такие как уравнения Бернулли, Риккати и др. При компьютерном моделировании, как правило, ограничиваются получением численного решения, отвечающего конкретным значениям параметров. оно выводится в виде графика или соответствующего массива числовых данных.
2. Построение математических моделей динамических систем
Первый шаг при моделировании динамических систем состоит в переходе от физической или технической задачи к ее математической модели в виде дифференциального уравнения или системы таких уравнений. При этом используются теория и законы соответствующей предметной области, например, при моделировании механических систем это законы ньютона и сохранения энергии; при моделировании электрических схем – законы Ома и Кирхгофа и т. п. Поясним процедуру построения математической модели динамических систем на нескольких примерах.
Пример 1.1. Математический маятник. Рассмотрим маятник массы т и длины l, который совершает малые колебания около положения равновесия (pис. 1.2). Требуется найти дифференциальное уравнение, описывающее колебания этой механической системы.
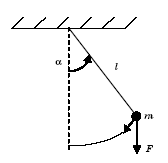
Рис. 1.2. Математический маятник
Для построения математической модели воспользуемся формулой второго закона Ньютона F = та, где F – сила, действующая на материальную точку вдоль касательной к траектории; 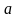 – линейное ускорение материальной точки.
– линейное ускорение материальной точки.
Обозначим угловое отклонение маятника α(t), тогда
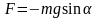 .
.
Линейное ускорение 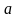 связано с угловым ускорением
связано с угловым ускорением 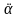 соотношением
соотношением 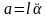 .
.
Подставляя эти выражения в уравнение 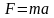 , получаем
, получаем
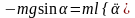 или
или 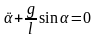 .
.
Это нелинейное дифференциальное уравнение второго порядка.
В случае малых колебаний замена 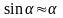 приводит к линейному дифференциальному уравнению
приводит к линейному дифференциальному уравнению
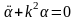 ,
, 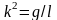 . (1.1)
. (1.1)
Пример 1.2. Резервуары с жидкостью. Рассмотрим задачу о протекании жидкости через три сообщающихся сосуда (рис. 1.3). Обозначим уровни жидкости в сосудах через x1(t), x2(t), x3(t) и будем считать, что в начальный момент времени жидкость была только в первом сосуде, т. е. х1(0) = m, х2 (0) = х3(0) = 0. Очевидно, что с течением времени х1 будет убывать, а х3 – возрастать. Уровень х2 сначала будет расти, а затем, начиная с некоторого момента времени t1, уменьшаться.
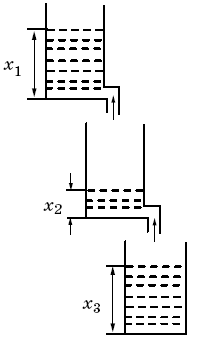
Рис.1.3. Три резервуара
Полагая скорость вытекания жидкости пропорциональной ее количеству, получаем, что процесс может быть описан системой трех дифференциальных уравнений
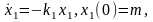
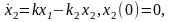 (1.2)
(1.2)
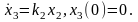
Левые части уравнений (1.2) соответствуют скоростям изменения уровней жидкости в сосудах, положительные и отрицательные слагаемые в правых частях уравнений характеризуют количество прироста и убыли жидкости. например, слагаемое k1х1 во втором уравнении отражает приток жидкости во второй сосуд из первого, а слагаемое –k2х2 отражает ее вытекание из второго сосуда в третий.
Уравнения (1.2) можно переписать в матричной форме
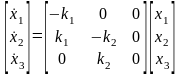 ,
, 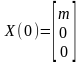 . (1.3)
. (1.3)
Эту модель можно усложнить, учитывая возможность пополнения жидкости в первом сосуде и вытекания ее из третьего сосуда.
Пример 1.3. Система «загрязнение-окружающая среда». Пусть рассматривается замкнутая система загрязнение – природа. В первом приближении состояние этой системы можно описать парой чисел 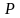 и
и 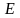 , где
, где 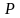 – характеристика общего уровня загрязнения в рассматриваемой области, а
– характеристика общего уровня загрязнения в рассматриваемой области, а 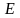 – характеристика окружающей среды (например, плотность биомассы).
– характеристика окружающей среды (например, плотность биомассы).
Предположим, что имеется постоянный источник загрязнения. Загрязнение отрицательно влияет на окружающую среду. Пусть окружающая среда способна перерабатывать загрязнение до определенного предела. Тогда динамика системы загрязнение – окружающая среда можно описать следующей системой обыкновенных дифференциальных уравнений:
(1.4)
где 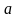 - мощность источника загрязнения за единицу времени,
- мощность источника загрязнения за единицу времени,  - коэффициент линейного «мертвого» уничтожения загрязнения (естественная диссипация),
- коэффициент линейного «мертвого» уничтожения загрязнения (естественная диссипация),  - функциональный член, описывающий абсорбирование и переработку загрязнений окружающей средой,
- функциональный член, описывающий абсорбирование и переработку загрязнений окружающей средой,  - член, описывающий динамику состояния окружающей среды в отсутствие загрязнения,
- член, описывающий динамику состояния окружающей среды в отсутствие загрязнения,  - член, описывающий деструктивное влияние загрязнения на окружающую среду.
- член, описывающий деструктивное влияние загрязнения на окружающую среду.








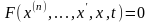 .
.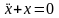 и
и 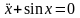 . Первое из них – линейное, оно приближенно описывает малые колебания математического маятника, второе (нелинейное) описывает колебания произвольной амплитуды.
. Первое из них – линейное, оно приближенно описывает малые колебания математического маятника, второе (нелинейное) описывает колебания произвольной амплитуды.
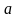 – линейное ускорение материальной точки.
– линейное ускорение материальной точки. 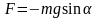 .
.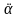 соотношением
соотношением 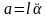 .
.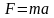 , получаем
, получаем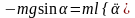 или
или 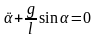 .
.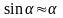 приводит к линейному дифференциальному уравнению
приводит к линейному дифференциальному уравнению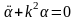 ,
, 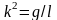 . (1.1)
. (1.1)
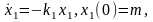
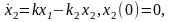 (1.2)
(1.2)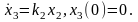
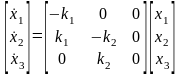 ,
, 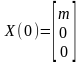 . (1.3)
. (1.3)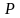 и
и 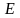 , где
, где 









