Муниципальное общеобразовательное учреждение
Средняя общеобразовательная школа 17
имениА.А. Герасимова
Исследовательская работа по теме
«Математические розы»
Выполнила: Бакаутова Дарья, ученица 10 класса.
Научный руководитель:
Качалова Елена Сергеевна.
г. Рыбинск
2022г.
Содержание:
| 1. | Введение. Цель и задачи работы ……………………………… | 2 |
| 2. | Основная часть…………………………………………………... | 3 |
|
| 2.1 | Полярная система координат……………………………. | 3 |
|
| 2.2 | Математические розы……………………………………... | 4 |
|
|
| 2.2.1 | Что такое математические розы………………… | 4 |
|
|
| 2.2.2 | Виды и уравнения математических роз………... | 4-7 |
|
|
| 2.2.3 | Исследование применения математических роз в природе и жизни человека………………………
|
7-8 |
| 3. | Исследование и построение математических роз……………. | 9 |
| 4. | Заключение……………………………………………………….. | 10 |
| 5. | Интернет источники…………………………………………….. | 11 |
| 6. | Приложения………………………………………………………. | 12-13 |
Введение.
Тема проекта:Математические розы
Актуальность темы заключается в демонстрации и применении математических знаний в практической деятельности человека.
Люди различают окружающие их вещи по форме. Интерес к форме предмета может быть вызван какой-либо потребностью у человека, а может и красотой самой формы.
Форма, воснове построения которой лежат сочетание симметрии и золотого сечения, способствует наилучшему зрительному восприятию и появлению ощущения красоты и гармонии у человека.
Цель:Изучение математических роз.Анализ видов роз, известных в математике, рассмотрение объектов, имеющих вид роз, а также изучение основных понятий полярной системы координат, методов построениякривых в полярной системе координат.
Задачи:
Изучениеинтернет источников.
Изучение основных понятий полярной системы координат.
Развитие умений и навыков по построению линий в полярной системе координат.
Анализ интернет - ресурсов по теме розы в математике.
Рассмотрение объектов, имеющих вид роз, с которыми человек встречается ежедневно и использует в своей деятельности
Построение математических роз.
2.Основная часть.
2.1 Полярная система координат.
Полярная система координат — двухмерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом. Полярная система координат особенно полезна в случаях, когда отношения между точками проще изобразить в виде радиусов и углов; в более распространённой, декартовой или прямоугольной системе координат, такие отношения можно установить только путём применения тригонометрических уравнений (рис.1)
Полярная система координат задаётся лучом, который называют нулевым или полярной осью. Точка, из которой выходит этот луч, называется началом координат или полюсом. Точка на плоскости определяется радиальной полярной координатой. Радиальная координата (обычно обозначается ϕ и соответствует расстоянию от точки до начала координат). Определённая таким образом радиальная координата может принимать значения от нуля до бесконечности.Положительным направлением отсчета углов считается направление «против часовой стрелки»(рис. 2)
Основными понятиями этой системы являются точка отсчёта – полюс, и луч, начинающийся в этой точке – полярная ось. Полярный радиус ρ – длина отрезка ОP. Полярный угол φ – величина угла между полярной осью и отрезком ОX и OP. (Приложение 1.)
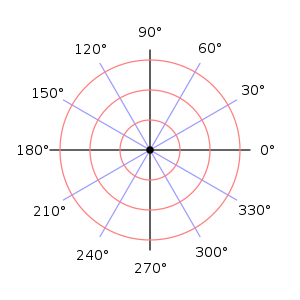
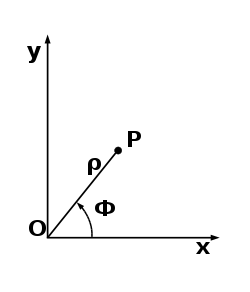
Рис.1 Рис.2
2.2 Математические розы.
2.2.1Что же такое математические розы.
Математические розы – плоские кривые, напоминающие символическоеизображение цветка. (рис. 3 и 4).
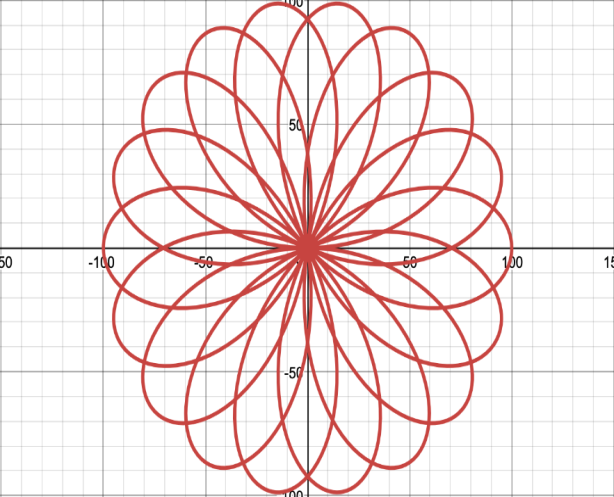
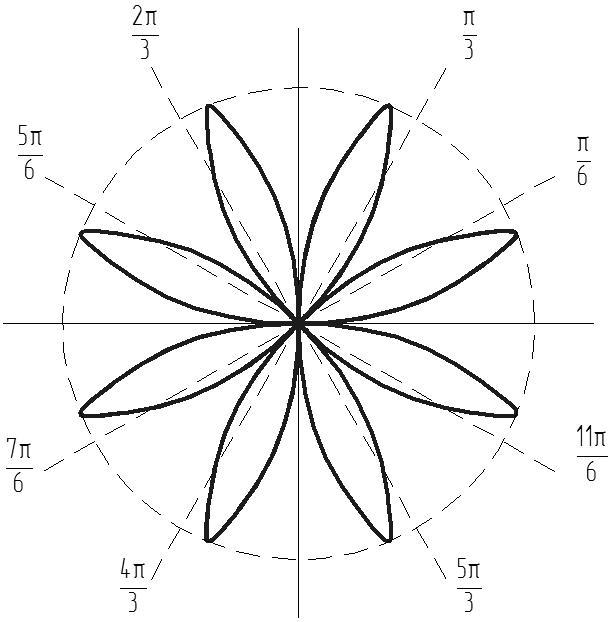
Рис. 3 Рис.4
2.2.2Виды и уравнения математических роз.
Роза Гвидо Гранди
Уравнение данной розы:ρ=asinkφ.
Здесь a{\displaystyle a} иk {\displaystyle k}— постоянные, определяющие размер (a) и количество лепестков (k) данной розы. Вся кривая располагается внутри окружности радиуса a {\displaystyle a}aaaи в случае k 1 состоит из одинаковых по форме и размеру лепестков. Количество лепестков в данном случае определяется величиной k.{\displaystyle k}//
Задавая параметр k=n/d, отношением натуральных чисел, можно получить замкнутые кривые, при определенных условиях превращающиеся в лепестковые цветы или в ажурные розетки, которые могут служить элементами декора или орнамента. Изменяя данное уравнение, а также подставляя в него множество чисел можно получить огромное разнообразие роз (рис.5).
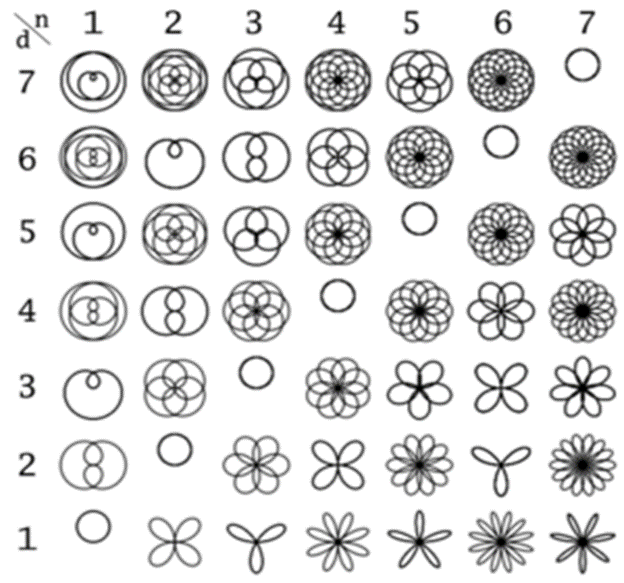
Рис.5
Семейство роз Гранди имеет свойство, которое в природе не сразу и заметишь, так как:Если k=n/d, то вся кривая расположена внутри круга единичного радиуса. В силу периодичности тригонометрических функций роза состоит из одинаковых лепестков, симметричных относительно наибольших радиусов, каждый из которых равен.
1. ρ=α sin2φ 2. ρ=α sin3φ
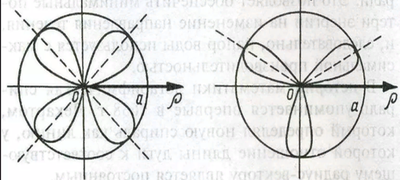
Рис.6
Наиболее красивые «цветы» получаются при k=4(четырехлепестковая роза) и при k=3 (трёхлепестковая роза, хотя многим, кто смотрит на данную розу, кажется, что это кривая напоминает пропеллер).(рис.6).
Полярная роза
Полярная роза – известная математическая кривая, похожая на цветок.
В полярных координатах определяется уравнением: ρ=2 sin4φ(рис.7).
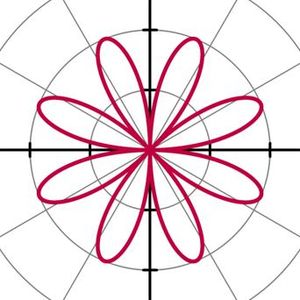
Рис.7
Кардиоида
Кардиоида – получила свое название из-за схожести своих очертаний со стилизованным изображением сердца.
Определяется в полярных координатах уравнением: ρ=α(1-cos φ), в котором α – радиус окружности (рис.8 и 9).
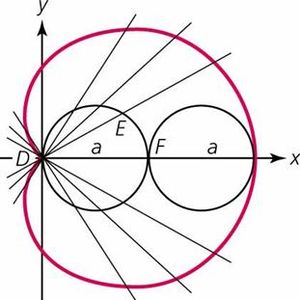
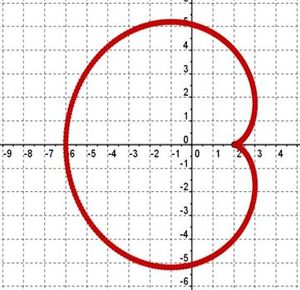
Рис.8 Рис.9
Лемниската Бернулли
Лемниската Бернулли – кривая, у которой произведение расстояний каждой ее точки до двух заданных точек (фокусов) - постоянно и равно квадрату половины расстояния между ними (рис.10).
Уравнение: ρ^2=2с^2 cos 2φ

Рис.10
2.2.3Исследование применения математических роз в природе и жизни человека
Большинство видов математических роз встречается в архитектуре, в создании человеком храмов, церквей и т.д.(рис.11 и 12).


Рис.11 Рис.12
С помощью выращенных цветов, различных кривых и графических редакторов можно сделать, например, различные рисунки, рамки-орнаменты или украсить ими различные предметы. Орнамент – украшение, узор, состоящий из ритмически организованных повторяющихся элементов, которые композиционно могут образовывать орнаментальный ряд или раппорт (рис.13 и 14).


Рис.13 Рис.14


Рис.15 Рис.16


Рис.17 Рис.18
3.Исследование и построение математических роз.
При работе над данной темой мне стало интересно как выглядят некоторые, изучаемые в школьном курсе математики, графики функций в полярной системе координат. И я начала с самых простых. При этом мною были сделаны следующие основные выводы.
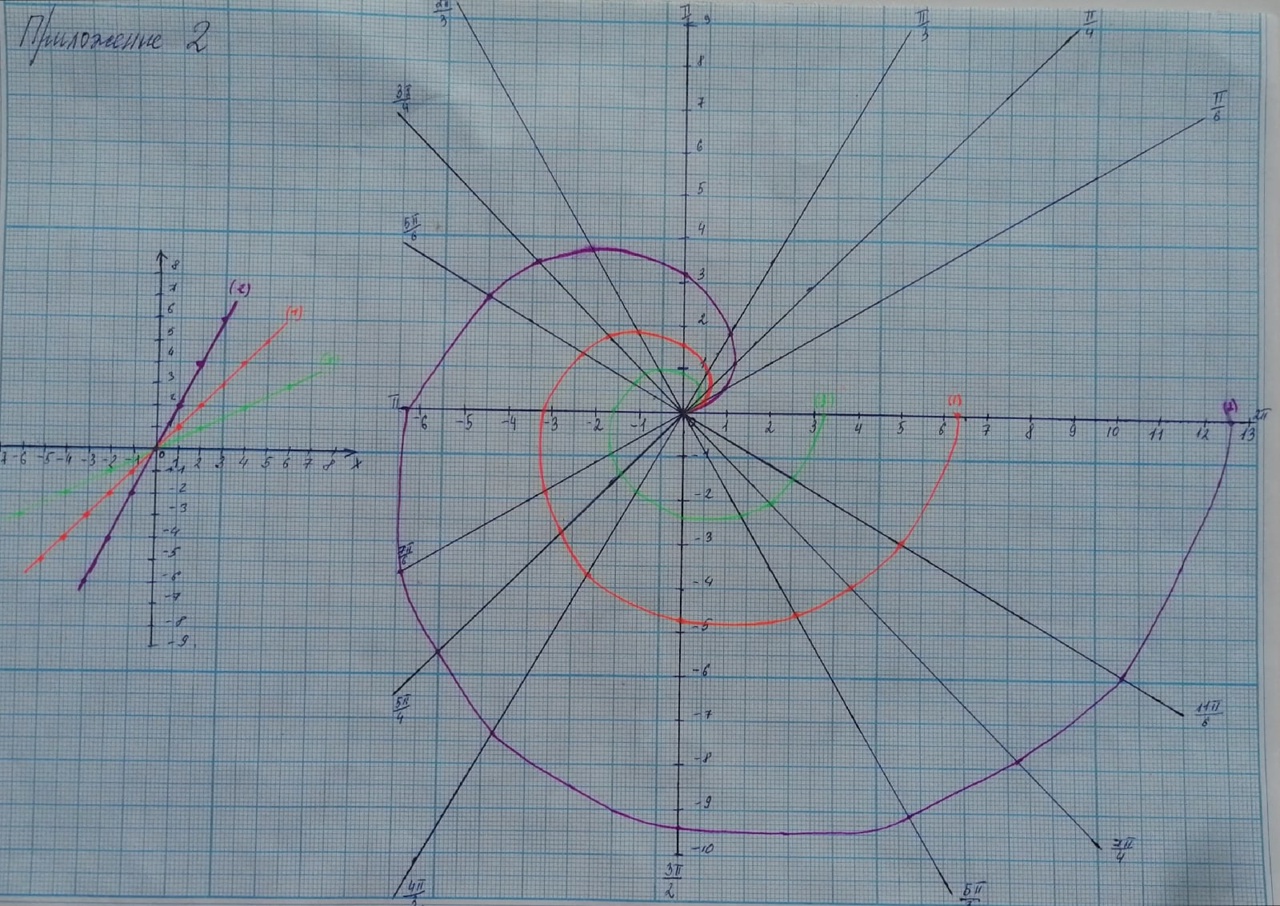
Построив график линейно функции в полярной системе координат, были получены спирали. Тогда как в привычной нам декартовой системе это прямые. (Приложение 2). В спирали полярный радиус зависит от полярного угла φ. Если мы увеличим угол в два раза, то спираль будет расширяться, а если уменьшим в два раза, то сужаться.
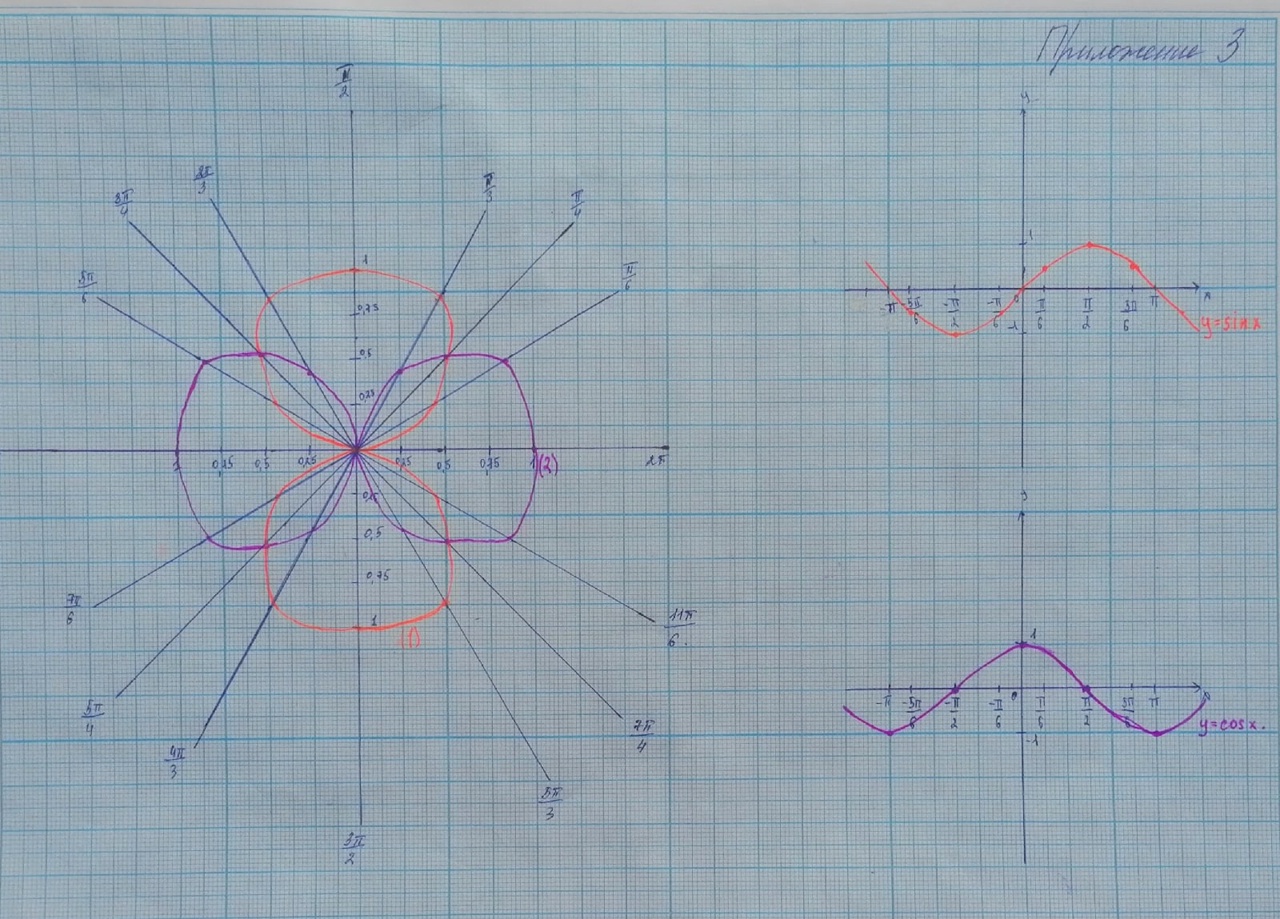
Знакомая нам синусоида в декартовой системе координат, в полярной напоминает розу с двумя лепестками, расположенными вдоль вертикальной оси. Косинусоида также напоминает двухлепестковую розу, расположенную вдоль горизонтальной оси (Приложение 3).
Количество лепестков у розы зависит от числа k. Если число k равно 1, то 2 лепестка. Если k равно 2, то количество лепестков удваивается (равно 4) и т.д. (Приложение 4).
Если увеличивать число а, то лепестки розы будут сужаться и удлиняться вдоль осей координат (Приложение 4).
Заключение.
Из всей данной работы можно сделать вывод, что розы занимают важную и значимую роль в нашей жизни. Без них было бы невозможно существование многих растений.Так же без знания таких фигур люди не смогли бы воспроизводить данную красоту в архитектуре, ландшафтном дизайне и любой другой своей деятельности.
Проведя исследование на данную тему, я узнала много интересного связанного с математическими расчётами, розами, об их значениях и проявлениях в природе и деятельности человека. Научилась делать построение некоторых фигур, и в итоге пришла к выводу, что всё всегда связано с окружающим нас миром, и ничего не возникает из ниоткуда.
Практическая значимость работы: Данное исследование можно применять на факультативных занятиях по математике.
Цель работы достигнута: определена значимая роль математических кривых – роз в жизни человека. Гипотеза о том, что розы присутствуют в каждом аспекте нашей жизни, подтверждена. Все поставленные в работе задачи решены: проведен анализ видов роз известных в математике, рассмотрены объекты, с которыми человек встречается ежедневно и использует в своей деятельности, проведено построение математических роз, изучено понятие полярных координат и их построения.
Интернет источники.
https://nsportal.ru/ap/library/nauchno-tekhnicheskoe-tvorchestvo/2015/07/19/issledovatelskaya-rabota-matematicheskiy
https://vuzlit.com/847251/krivye_polyarnyh_koordinatah_kohleoida_strofoida_spiral_arhimeda_logarifmicheskaya_spiral
https://www.prodlenka.org/metodicheskie-razrabotki/413965-issledovatelskaja-rabota-matematicheskij-cvet
https://infourok.ru/proekt-zamechatelnie-krivierozi-i-spirali-3776420.html
https://obuchonok.ru/node/6009
https://en.ppt-online.org/553475
https://school-science.ru/5/7/34989
Приложения
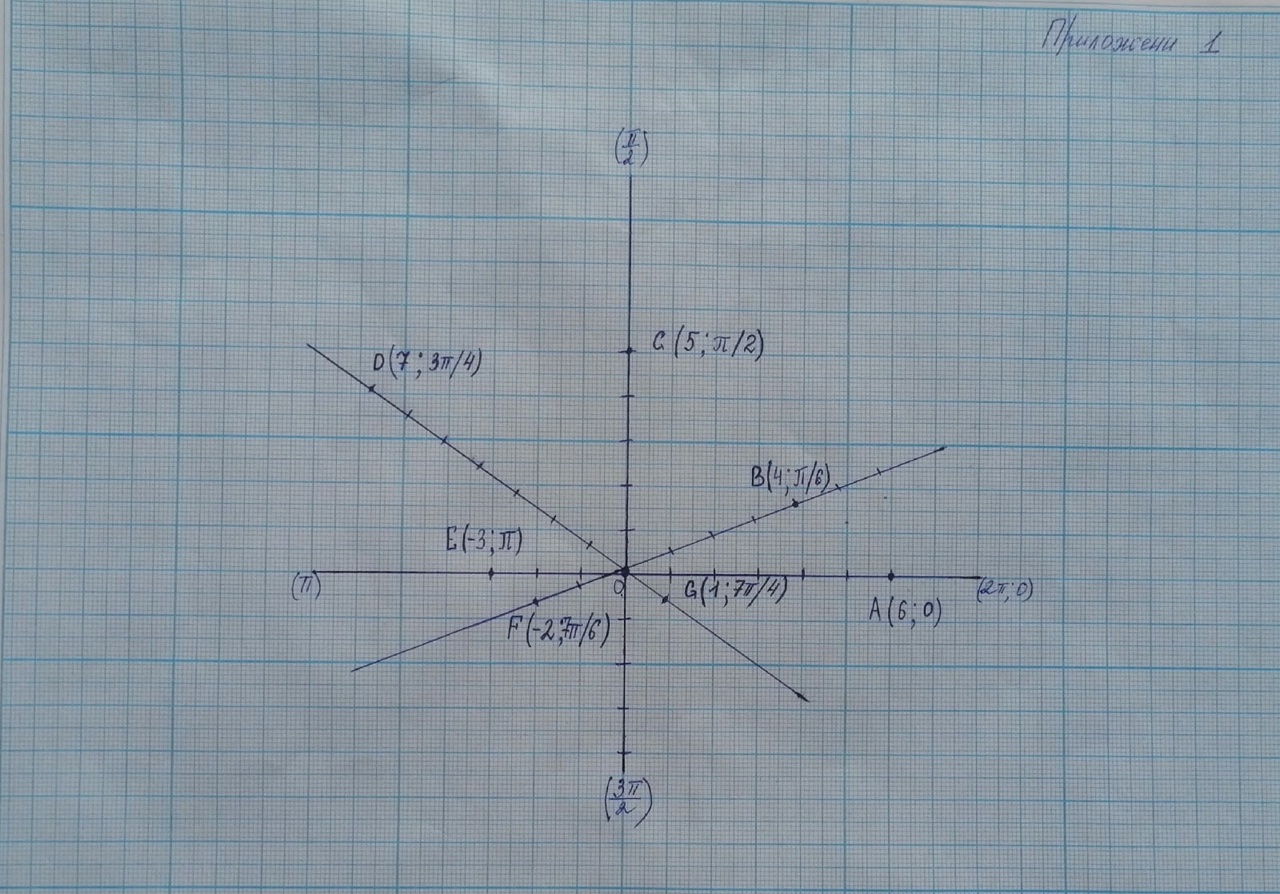
Приложение 1.
Примеры построения точек в полярной системе координат.
Приложение 2
Спирали.
Приложение 3.
Косинусоид и синусоид.
Приложение 4
Математические роза.

12






































