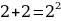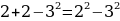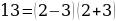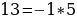| Муниципальное бюджетное оБщеобразовательное учреждение «Центр образования №22 – Лицей искусств» г.Тула |
| Математические софизмы |
|
|
|
|
| Проект выполнила: ученица 10 В класса Юлина Карина Руководитель проекта: учитель математики Сватковская Е.А. |
|
|
Содержание:
Паспорт проекта.
Введение. Цели, задачи проекта.
Глава первая. Понятие софизма.
История софизмов.Виды софизмов.
Классы ошибок в софизмах.
Глава вторая. Виды математических софизмов:
логические софизмы.
алгебраические софизмы.
геометрические софизмы.
Глава третья. Как создать софизм?
Принципы, по которым составляются софизмы.
Создание своего софизма.
Заключение
Приложение
Введение.
Всем нам хоть раз в жизни встречались высказывания, такие как «Дважды два равно пять», «Два равно трем». Откуда взялись эти утверждения? Кто их придумал? Можно ли их объяснить или это просто выдумка?
В своей работе я хочу разобраться в вопросах, связанных с математическими софизмами. Математические софизмы, по моему мнению, интереснее других своей четкостью и логичностью объяснения. И мы сталкиваемся с ними намного чаще, чем с другими софизмами.
Софизмы заставляют нас думать в различных направлениях и рассматривать проблемы с разных сторон, анализируя небольшие детали. И еще, софизм – это обман, который не каждый сможет распознать, а, следовательно, люди обманывают друг друга с помощью софизмов. Так происходит и в наше время, и происходило тысячелетия назад.
Цель моего проекта - изучение математических софизмов
Задачи:
1.Найти, изучить и проанализировать информацию, полученную при изучении софизмов.
2. Изучить историю софизмов.
3.Рассмотреть виды софизмов, выявить ошибки в математических софизмах.
4. Разделить на классы математические софизмы.
5. Разобрать логику составления и решения математических софизмов.
6. Создать собственный софизм.
7. Привлечь интерес учащихся к урокам математики.
Объект проекта: софизмы.
Предмет проекта: математические софизмы.
В этой работе былииспользованы некоторые примеры алгебраических, геометрических, логических софизмов из книг «Что не так?» Львовского С.М., «Математические софизмы» Обреимова В.И., «Математические софизмы» А.Г. Мадеры, Д.А. Мадеры1. Так же из “Математической шкатулки” Ф.Ф. Нагибина, Е.С. Канина2 взяли историю развития математических софизмов.
Методы исследования: определение понятий, анализ и синтез.
Практическая значимость: Видеть и замечать неявные ошибки, акцентировать внимание на мелких деталях.Данный материал можно применять на факультативных занятиях, математическом кружке, чтобы привить интерес учащихся к математике.
Глава первая. Понятие софизма.
История возникновения софизмов.
Сам софизм был введен древнегреческим софистами в V в. до н.э. как пример обучения.Софисты были личными наёмными учителями и опирались на решение задач.
Аристотель не считал софизмы научным поиском истины, а «натаскиванием» и составил в книге «О софистических опровержениях» первую классификацию софизмов, выделив 13 видов софизмов, возникающих из-за двусмысленностей двоякого рода, 6, связанных с оборотами речи, и 7 паралогизмов или неправильно построенных рассуждений.
Аристотель софизмом называл «мнимые доказательства», убедительность многих софизмов, их «логичность» обычно связана с хорошо замаскированной ошибкой:
семантической: возникает за счёт нарушения однозначности мысли и приводит к смешению значений терминов;
логической: подмена основной мысли доказательства, принятие лжи за истину, несоблюдение допустимых способов рассуждения, использование «неразрешённых» или даже «запрещённых» правил или действий, например деления на нуль в математических софизмах.
В истории математические софизмы играли существенную роль: уяснение ошибок в математических рассуждениях часто содействовало развитию математики.
Особенно поучительна в этом отношении аксиомао параллельных прямых Евклида. Звучит она так: через данную точку, лежащую вне данной прямой, можно провести не более одной прямой, параллельной данной. На протяжении двух тысяч лет многие выдающиеся математики пытались это доказать, пытались это вывести из аксиом геометрии. Но попытки не увенчались успехом. Многочисленные «доказательства» оказались ошибочными. И все же они принесли огромную пользу в развитии геометрии: выяснились связи между разными теориями геометрии; тем самым была подготовлена почва для создания Неевклидовой геометрии.3
Виды софизмов
Существует довольно большое количество видов софизмов. Вот некоторые из них:
логические;
терминологические;
психологические;
интеллектуальные;
аффективные;
волевые;
математические;
исторические.
Классы ошибок в софизмах.
В софизмах ученые выделяют 3 класса ошибок:
1. Логические ошибки.
Так как вывод может быть выражен в силлогистической форме, то и любой софизм может сводиться к нарушению правил силлогизма. Наиболее часто к логическим софизмам приводят нарушения следующих правил:
вывод с отрицательной меньшей посылкой в первой фигуре: «Все люди суть разумные существа, жители планет не суть люди, следовательно, они не суть разумные существа»;
вывод с утвердительными посылками во второй фигуре: «Все, находящие эту женщину невинной, должны быть против наказания её; вы — против наказания её, значит, вы находите её невинной»;
вывод с общим заключением в третьей фигуре: «Закон Моисеев запрещал воровство, закон Моисеев потерял свою силу, следовательно, воровство не запрещено».
2. Терминологические ошибки.
Больше всего распространены ошибки употребления среднего термина в большой и в меньшей посылке не в одинаковом значении.
Грамматические, терминологические и риторические источники софизмов выражаются в неточном или неправильном словоупотреблении и построении фразы. Существует несколько классов терминологических ошибок:
ошибка омонимии;
ошибка сложения — когда разделительному термину придается значение собирательного;
ошибка разделения (обратная), когда собирательному термину дается значение разделительного;
ошибка ударения, когда подчёркивание повышением голоса в речи и курсивом в письме определенного слова или нескольких слов во фразе искажает её первоначальный смысл;
ошибка выражения, заключающаяся в неправильном или неясном для уразумения смысла построении фразы.
Более сложные софизмы происходят из неправильного построенного ряда доказательств, где ошибки являются тенью всего выражения.
3. Психологические ошибки.
Психологические причины софизмов бывают троякого рода: интеллектуальные, аффективные и волевые. Во всяком обмене мыслей предполагается взаимодействие между 2 лицами, читателем и автором или лектором и слушателем, или двумя спорящими. Убедительность софизма предполагает два фактора: α — психические свойства одной и β — другой из обменивающихся мыслями сторон. Правдоподобность софизма зависит от ловкости того, кто защищает его, и уступчивости оппонента, а эти свойства зависят от различных особенностей обеих индивидуальностей.
4. Интеллектуальные причины.
Интеллектуальные причины софизма заключаются в преобладании в уме лица, поддающегося софизму, ассоциаций по смежности над ассоциациями по сходству, в отсутствии развития способности управлять вниманием, активно мыслить, в слабой памяти, непривычке к точному словоупотреблению, бедности фактических знаний по данному предмету, лености в мышлении (ignavaratio). Обратные качества, разумеется, являются наиболее выгодными для лица, защищающего софизм: обозначим первые отрицательные качества через b, вторые соответствующие им положительные через а.
5. Аффективные причины.
Сюда относятся трусость в мышлении — боязнь опасных практических последствий, вытекающих от принятия известного положения; надежда найти факты, подтверждающие ценные для нас взгляды, побуждающая нас видеть эти факты там, где их нет, любовь и ненависть, прочно ассоциировавшиеся с известными представлениями. Желающий обольстить ум своего соперника софист должен быть не только искусным диалектиком, но и знатоком человеческого сердца, умеющим виртуозно распоряжаться чужими страстями для своих целей.
6. Волевые причины.
При обмене мнений мы воздействуем не только на ум и чувства собеседника, но и на его волю. Во всякой аргументации (особенно устной) есть элемент волевой — императивный — элемент внушения. Категоричность тона, не допускающего возражения, определенная мимика действуют неотразимым образом на лице, легко поддающихся внушению, особенно на массы, с другой стороны, пассивность слушателя особенно благоприятствует успешности аргументации противника. Логические, грамматические и психологические факторы теснейшим образом связаны между собой.
Таким образом, софизмы - довольно древнее понятие. Существует множество видов софизмов. Но всех их объединяют схожие «ошибки». Попытки разгадать математические софизмы приводят к более полному понятию математики.
Глава вторая. Виды математических софизмов.
1) Логические софизмы.
Начнем с небольшого английского софизма в качестве разминки:
The more you study – the more you know,
The more you know – the more you forget,
The more you forget – the less you know,
The less you know – the less you forget,
The less you forget – the more you know.
Why study?4
(Чем больше мы учим, тем больше знаем.
Чем больше мы знаем, тем больше забываем.
Чем больше мы забываем, тем меньше знаем.
Чем меньше мы знаем, тем меньше забываем.
Чем меньше забываем, тем больше знаем.
Зачем учиться?)
Следующий софизм довольно прост. Для начала познакомимся с одним занимательным парадоксом:
В один раз хозяину гостиницы с бесконечным, но счетным числом номеров, которые не были свободны, нужно было принять нового гостя. Хозяин нашел очень простой выход: он каждого из постояльцев переселил в комнату, номер которой был на единицу больше, чем номер прежней комнаты. В итоге, каждый обитатель n-й комнаты переехал в (n+1)-ю и освободил первую комнату для нового гостя. Как поступить хозяину, если к немуприедут бесконечно много гостей? Все также, хозяину просто требуется переместить всех прежних жильцов в (n*2) и разместить новых гостей в освободившиеся нечетные номера.Возможно ли, разместить новых гостей хозяину, при этом, не имея счетное количество комнат?
Во взятом нами софизмом рассказывается о хитром хозяине гостиницы, разместившем в девяти номерах десять гостей так, что каждому досталась одна комната:
Их было десять чудаков,
Тех спутников усталых,
Что в дверь решили постучать
Таверны «Славный малый».
«Пусти, хозяин, ночевать,
Не будешь ты в убытке,
Нам только ночку переспать,
Промокли мы до нитки».
Хозяин тем гостям был рад,
Да вот беда некстати:
Лишь девять комнат у него
И девять лишь кроватей.
«Восьми гостям я предложу
Постели честь по чести,
А двум придется ночь проспать
В одной кровати вместе».
Лишь он сказал, и сразу крик,
От гнева красны лица.
Никто из всех десятерых
Не хочет потесниться.
Как охладить страстей тех пыл,
Умерить те волненья?
Но старый плут хозяин был
И разрешил сомненья.
Двух первых путников пока,
Чтоб не судили строго,
Просил пойти он в номер «А»
И подождать немного.
Спал третий в «Б», четвертый в «В»,
В «Г» спал всю ночь наш пятый,
В «Д», «Е», «Ж», «3» нашли ночлег
С шестого по девятый.
Потом, вернувшись снова в «А»,
Где ждали его двое,
Он ключ от «И» вручить был рад Десятому герою.
Хоть много лет с тех пор прошло,
Неясно никому,
Как смог хозяин разместить
Гостей по одному.
Иль арифметика стара,
Иль чудо перед нами,
Понять, что, как и почему,
Вы постарайтесь сами.
В чем же тут ошибка? А все очень просто, мы просто забыли про десятого, точнее хозяин вернулся к первым двум, и отдал ключ одному из них, но поселил он девятерых и отдал, допустим, второму ключ от комнаты «И», но десятый тут никак не фигурирует.
4 рубля = 40000копейкам
Возьмем верное равенств:
2 рубля = 200 копейкам и возведем его по частям в квадрат.
Мы получим: 4 рубля = 40000 копейкам.5
В чем же ошибка? Вот в чем: возведение в квадрат денег не имеет смысла. В квадрат возводятся числа, а не величины.
Существует множество логических софизмов и можно найти даже такие у которых объяснение будет неоднозначным, вот пример такого:
«Учебная тревога»
Однажды командир Н-ской роты объявил солдатам следующее:
— В один из рабочих дней на следующей неделе в 5 часов утра у нас будет учебная тревога. Чтобы приблизить обстановку к боевой, эта тревога будет для вас неожиданной: пока ее не объявят, вы не будете знать, что она состоится именно в этот день.
Вечером того же дня рядовой Петров объяснял своим товарищам:
— Я все понял: никакой тревоги не будет, нам только голову морочат! Вот смотрите. В пятницу эту тревогу объявить не могут: ведь тогда уже в четверг вечером мы будем знать, что тревога будет именно в пятницу – другого-то дня не остается! А нам ведь объявили, что нам до последнего момента будет неизвестно, в какой день будет тревога, так что пятница исключается. Но могут ли объявить тревогу в четверг? Тоже нет! Ведь если в первые три дня тревоги не будет, то мы уже в среду вечером будем знать, что тревога будет в четверг или пятницу, а так как в пятницу ее объявить не могут, остается только четверг, и мы опять узнаем дату тревоги заранее, неожиданности не будет. Значит, остаются только понедельник, вторник и среда, но тут мы рассуждаем точно так же: в среду объявить тревогу невозможно, ну и так далее. Так что обойдемся без тревоги.
Рассуждение рядового Петрова всех убедило. Однако же в среду в пять утра по казарме разнеслось: «Рота, подъем! Тревога!». Как вы понимаете, для всех, включая рядового Петрова, это оказалось полной неожиданностью, так что все случилось в соответствии с тем, что объявил командир роты.
Но где же тогда ошибка в рассуждениях рядового Петрова?6
И правда, в чем же ошибся рядовой?
Есть два варианта «решения» этого вопроса.
Первое объяснение, заключается в том, что Петров ошибся в самом начале своих рассуждений. Ведь вполне возможно в пятницу провести тревогу. Во-первых, потому что есть те, кто так же, как и Петров, посчитают пятницу неудачным днем для проведения «неожиданной» тревоги. Люди, опирающиеся на этот вывод, предполагают, прохождение учения раньше пятницы. Во-вторых, есть среди нас те, которые не задумываются о следующем дне, так для них тревога будет тоже неожиданной.
Петров считает, что предсказуемое событие никак не может быть неожиданным. Но саму тревогу объявляет человек, а действия его точно предсказать невозможно. Можно предугадать действия компьютерной программы, зная ее исходный код и исходные данные. У человека же есть воля.
Есть и другое объяснение не с логической точки зрения, а с житейской. Одинаковые слова, иногда, имеют разные значения в зависимости от ситуации. В нашем случае слово «неожиданный» различно в значениях. Для Петрова, как было ранее сказано, важным было значение «предугадать». А вот командир не имел в виду, что солдаты не смогут предсказать дату и время тревоги. Смысл его речи был намного проще: лишь предупредить их о планирующейся тревоге, чтобы они готовились.
2) Алгебраические софизмы
4=5
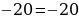
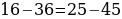
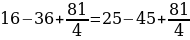
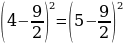
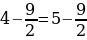
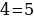
Ошибка: 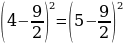
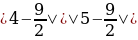
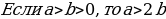
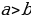 (натуральные числа)
(натуральные числа)
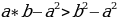
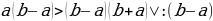
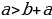
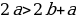
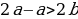
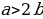
Ошибка: По условию 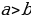 , значит
, значит 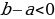 . При делении неравенства на отрицательное число, знак неравенства надо поменять, чего не было сделано.
. При делении неравенства на отрицательное число, знак неравенства надо поменять, чего не было сделано.
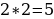
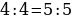
Вынесем за скобки общий множитель в каждой части:
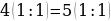
Числа в скобках равны, поэтому:
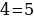
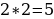
Ошибка допущена в вынесении общего множителя за скобки в левой и правой частях тождества 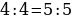 .
.
Отрицательноечисло больше положительного.
Возьмем два положительных числа a и b. Сравним два отношения: 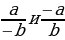 они равны, так как каждое из них равно
они равны, так как каждое из них равно 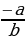 .Можно составить пропорцию:
.Можно составить пропорцию: 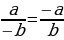 . Но если в пропорции предыдущий член первого отношения больше последующего, то предыдущий член второго отношения также больше своего последующего. В нашем случае
. Но если в пропорции предыдущий член первого отношения больше последующего, то предыдущий член второго отношения также больше своего последующего. В нашем случае 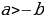 ; следовательно, должно быть
; следовательно, должно быть 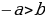 , т.е. отрицательное число больше положительного.
, т.е. отрицательное число больше положительного.
Ошибка заключается в том, что свойство (если в пропорции предыдущий член первого отношения больше последующего, то предыдущий член второго отношения также больше своего последующего) может оказаться неверным, если некоторые члены пропорции отрицательны.
Любое число равно числу, в два раза большему его.
Пусть 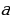 – какое угодно число. Возьмем тождество
– какое угодно число. Возьмем тождество 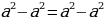 . В левой части его вынесем
. В левой части его вынесем 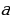 за скобки, а правую часть разложим на множители по формуле разности квадратов. Тогда получим:
за скобки, а правую часть разложим на множители по формуле разности квадратов. Тогда получим: 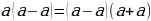 . Упростив это тождество, получим:
. Упростив это тождество, получим: 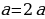 .
.
В уравнении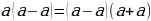 нельзя делить на
нельзя делить на 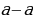 , т.к. это выражение будет равно нулю.
, т.к. это выражение будет равно нулю.
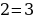
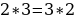
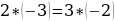
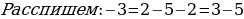
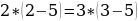
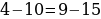
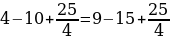
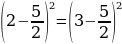
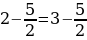
Увеличим обе части на 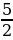 :
:
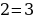
В чем же ошибка? Прибавляя к равным величинам равные, получаются равные суммы, но в этом случае величины не равны, посчитаем: 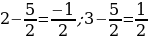 .Значит, в этом случае, если мы прибавим равные величины, то получим разные суммы.
.Значит, в этом случае, если мы прибавим равные величины, то получим разные суммы.
Следующий пример необычен тем, что он до сих пор не решен.
«Ахиллес никогда не догонит черепаху»
Древнегреческий философ Зенон доказывал, что Ахиллес, один из самых сильных и храбрых героев, осаждавших древнюю Трою, никогда не догонит черепаху, которая, как известно, отличается крайне медленной скоростью передвижения.
Вот примерная схема рассуждений Зенона:
Предположим, что Ахиллес и черепаха начинают движение одновременно, и Ахиллес стремится догнать черепаху. Примем для определённости, что Ахиллес движется в 10 раз быстрее черепахи, и что их отделяют друг от друга 100 шагов.
Когда Ахиллес пробежит расстояние в 100 шагов, отделяющие его от того места, откуда начала двигаться черепаха, то в этом месте он уже её не застанет, так как она пройдёт вперёд расстояние в 10 шагов. Когда Ахиллес пробежит и эти 10 шагов, то и там черепахи уже не будет, поскольку она успеет перейти на 1 шаг вперёд. Достигнув и этого места, Ахиллес опять не найдёт там черепахи, потому что она успеет пройти расстояние, равное 1/10 шага, и снова окажется несколько впереди его. Это рассуждение можно продолжать до бесконечности, и придётся признать, что быстроногий Ахиллес никогда не догонит медленно ползающую черепаху.
Где ошибка?
Софизм Зенона далек от своего конечного решения. Вот аспекты приведенные в книге Мадера А. Г., Мадера Д. А. «Математические софизмы»:
«Сначала определим время t, за которое Ахиллес догонит черепаху. Оно легко находится из уравнения a+vt=wt, где a – расстояние между Ахиллесом и черепахой до начала движения, v и w – скорости черепахи и Ахиллеса соответственно. Это время при принятых в софизме условиях (v=1 шаг/сек и w=10 шагов/сек) равно 11,111111… сек.
Другими словами, примерно через 11,1 сек. Ахиллес догонит черепаху.
Подойдём теперь к утверждениям софизма с точки зрения математики. Проследим логику Зенона. Предположим, что Ахиллес должен пройти столько же отрезков, сколько их пройдёт черепаха. Если черепаха до момента встречи с Ахиллесом пройдёт m отрезков, то Ахиллес должен пройти те же m отрезков плюс ещё один отрезок, который разделял их до начала движения. Следовательно, мы приходим к равенству m=m+1, что невозможно. Отсюда следует, что Ахиллес никогда не догонит черепаху.
Итак, путь, пройденный Ахиллесом, состоит из бесконечной последовательности отрезков, которые принимают бесконечный ряд значений.
Трудности, которые возникают при оперировании понятиями «непрерывного» и «бесконечного» до сих пор не определены, а разрешение противоречий, содержащихся в них, послужило более глубокому осмыслению основ математики».
Софизм Зенона справедлив в теории, но на практике не применим, довольно тяжело представить себе Ахиллеса, бегущего микроскопическое расстояние.7
3) Геометрические софизмы.
«Новое доказательство» теоремы Пифагора.
Возьмем прямоугольный треугольник с катетами 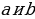 , гипотенузой
, гипотенузой 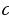
и острым углом 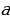 , противолежащим катету
, противолежащим катету 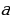 .
.

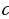
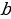

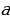
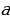
Имеем: 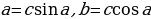 , откуда
, откуда 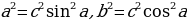 .
.
Просуммировав по частям эти равенства, получаем:
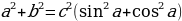 ,
,
но
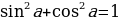 , и поэтому
, и поэтому 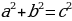 .
.
Здесь ошибка заключается в том, что формула 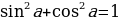 выводится на основании теоремы Пифагора, и поэтому в рассуждениях получается замкнутый круг.
выводится на основании теоремы Пифагора, и поэтому в рассуждениях получается замкнутый круг.
Ч
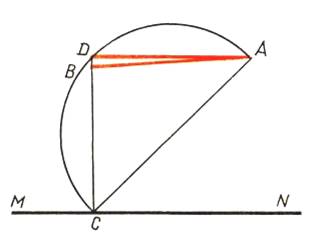
ерез точку, лежащую вне прямой, можно провести две прямые, параллельные данной прямой.
Дана пряма MN и вне ее точка A. Проведем через точку A прямую AB, параллельную прямой MN. Возьмем на MN некоторую точку C. На отрезке AC, как на диаметре, построим полуокружность. Пусть D – точка пересечения этой полуокружности с перпендикуляром к прямой MN, проходящим через точку C. Через точки A и D проведем прямую. Так как угол CDA прямой, а CD перпендикулярна MN, то AD – прямая, параллельная MN. Следовательно, через A проходят две прямые, параллельные прямой MN.
Ошибка: D принадлежит AB.
«Загадочный треугольник»
Дан прямоугольный треугольник 13*5 клеток, составленный из четырёх фигур.
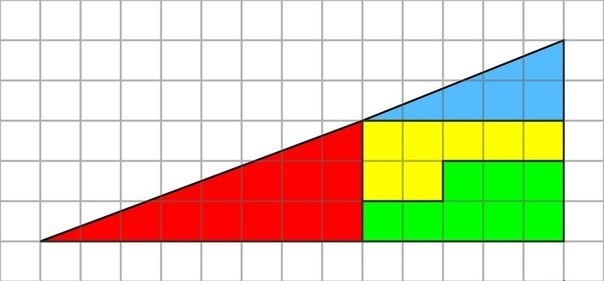 рис.1
рис.1
После перестановки фигур при визуальном сохранении изначальных пропорций появляется дополнительная, не занятая ни одной частью, клетка (рис. 2). Но мы же понимаем, что такого быть не может.
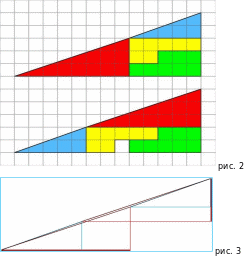
Площади закрашенных фигур, конечно, равны между собой (обе по 32 клетки), однако, то, что визуально наблюдается как треугольники 13*5, на самом деле таковым не является, и имеет разные площади. То есть ошибка, замаскированная в условии задачи, состоит в том, что начальная фигура названа треугольником (на самом деле являющаяся вогнутым четырёхугольником). Это отчётливо заметно на рис. 2 – гипотенузы верхней и нижней фигур проходят через разные точки: (8,3) вверху и (5,2) внизу. Секрет в свойствах синего и красного треугольников. Это легко проверить вычислениями.
Отношения длин соответствующих сторон синего и красного треугольников не равны друг другу(2\3 и 5\8), поэтому эти треугольники не являются подобными, а значит, имеют разные углы при соответствующих вершинах. Если нижние стороны этих треугольников параллельны, то гипотенузы в обоих треугольниках 13*5 на самом деле являются ломаными линиями (на верхнем рисунке создаётся излом внутрь, а на нижнем – наружу).Если наложить верхнюю и нижнюю фигуры 13*5 друг на друга, то между их гипотенузами образуется параллелограмм, в котором и содержится «лишняя» площадь. На рис. 3 этот параллелограмм приведён в верных пропорциях.
64=65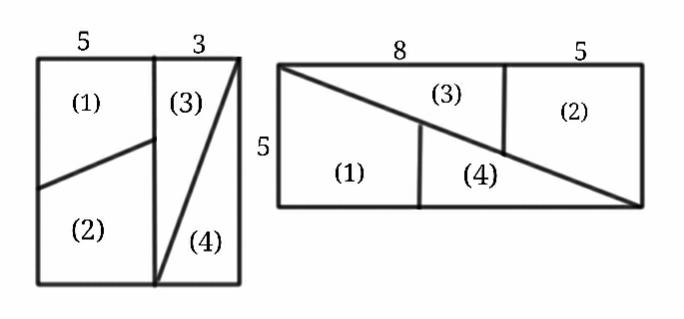
Квадрат со стороной, равной 8 единицам длины, разрезан на 4 части, как показано на рисунке выше. Из этих частей сложен прямоугольник. Основание этого прямоугольника оказалось равным 13 единицам длины, а высота – 5 единицам. Площадь исходного квадрата равна 64 квадратным единицам, а получившегося из него прямоугольника – 65 квадратным единицам. Значит, 64=65.
Ошибка: (1) и (4) части прямоугольника (отличного от квадрата) неплотно примыкают ко (2) и (3) частям его. Между ними образуется «щель» в виде вытянутого параллелограмма. Площадь этой щели как раз равна 1 квадратной единице.
Математические софизмы, какого бы вида они не были, всегда имеют логическое объяснение, и становятся сразу понятными, как только проанализировать их полностью. Даже имея некие «исключения» в виде неоднозначных и нерешенных софизмов, они все равно подтверждаются математическим путем.
Глава третья. Как создать софизм?
Принципы, по которым составляются софизмы.
Для начала берется какое-то равенство, неравенство, тождество,теорема или подчиняющееся логике выражение, и мы начинаем его менять - менять его стержень, подводя к использованию неправильных суждений. В математических софизмах это можно проворачивать согласно всем аксиомам, приведенным ниже.
Рассматривая каждый шаг преобразования, сможем найти «место» для ошибки. Хочу заметить, что большинство ошибок расположено в «спорных» случаях, в тех местах, где нужно помнить небольшие детали той или иной ситуации.
ОбреимовВ.И. в своей книге «Математические софизмы» обращается к следующим аксиомам:
Всякая величина равна самой себе;
Равные величины можно заменить равными;
Две величины, порознь равные третьей, равны между собой;
Если к равным величинам прибавить равные, то получатся равные суммы;
Если к равным величинам прибавить неравные, то получим неравные суммы, причем та сумма будет больше, которая получится от прибавления большей величины;
Если от равных величин отнимем равные, то получим равные разности;
Величина не измениться, если ее одновременно увеличить и уменьшить на одно и то же число:
Если равные величины умножить на равные же, то получим равные произведения;
Если равные величины помножить на неравные, то получим неравные произведения, причем то из произведений будет больше, которое поучится от умножения на большую величину;
Если равные величины разделим на равные, то получим равные частные;
Из двух отрицательных величин больше та, которой численное значение меньше;
Целое больше своей части;
Целое равно сумме всех своих частей;
Степени двух равных величин равны между собой;
Корни из двух равных величин равны между собой.8
Так же в его книге представлены общие «формулы», составления софизмов.
Логические софизмы - это какие-то истории, где рассуждения крутятся вокруг «стержня», который и является причиной рассуждений.
Создание своего софизма
Для начала стоит выбрать вид софизма. Я попробую взяться за алгебраические и логические софизмы.
Давайте начнем с алгебраических софизмов.
Возьмем один из софизмов, представленных ранее в части 2. Допустим, это будет софизм «Любое число равно числу, в два раза большему его». Первое, что мы можем сделать - это преобразовать конечный результат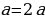 , нарушая правила, ведь делить на неизвестное нельзя, но эта ошибка работает только в буквенном виде. Получим:
, нарушая правила, ведь делить на неизвестное нельзя, но эта ошибка работает только в буквенном виде. Получим: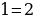 , и мы создали новый софизм. Правда, это не совсем новый софизм. Давайте подставим в софизм число 3:
, и мы создали новый софизм. Правда, это не совсем новый софизм. Давайте подставим в софизм число 3:
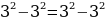
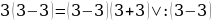
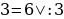
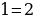
Мы получили новый софизм, ошибка которого заключается в том, что мы делим на (3-3), а эта скобка равна нулю = мы делим на ноль - чего делать, конечно же, нельзя.
Попробуем поиграть еще с одним софизмом.
Возьмем так же из части 2 софизм «2=3», но воспользуемся буквенным видом, представленном в книге «Математические софизмы» Обреимова В.И.9
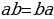















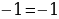
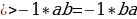
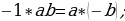
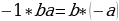
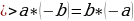
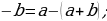
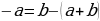
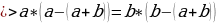
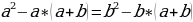
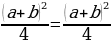
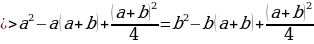
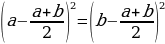
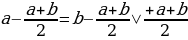
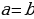
Теперь давайте в эту «формулу» подставим совершенно другие числа (не 2 и 3), пусть будет 5 и 7:
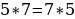
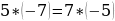
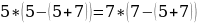
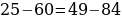
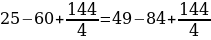
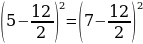
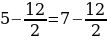
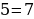
И вот наш «новый» софизм, основанный на уже имеющемся софизме.
Сейчас вам представиться софизм, который был самостоятельно составлен не из каких-то уже извесных «формул»:
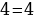
Разложим две части так, чтобы равенство было верным. И вычтем 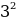 :
:
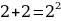
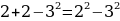
В левой стороне мы минус три возводим в квадрат, а в правой расскладываем по формуле разности квадратов:
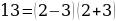
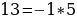
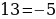
Ошибка в этом софизме довольно простая, но обычно многие ее допускают. Суть в том, что когда мы возводим в квадрат, минус в данном случае не принадлежит тройке, а играет роль именно знака.
Для логических софизмов нам нужно придумать логично-нелогичную сказку.
Вот первый вариант моей «сказки»:
На день рождения Оле подарили торт, разрезанный на двенадцать частей. К ней пришло пятеро друзей, она дала каждому по кусочку, следом пришли тетя, дядя, бабушка и дедушка, и ушло три человека. К тому времени подоспели еще пятеро гостей. И каждому досталось по кусочку. Но как такое может быть? Ведь кусочков было 12, а ели торт 15 человек.
В этом примере ошибка в том, что мы вернули три уже съеденых кусочка, такого, конечно же, не может быть.
И вот второй вариант, с теми же числами:
В концертном зале осталось двенадцать мест. Пришло шесть человек, они заняли свободные места, к первому звонку пришло еще четыре человека и вышло три. К началу концерта подоспели еще пять человек, сели на свободные места и три человека вернулись, заняв свои места. Вот так вот на твенадцати местах уместилось пятнадцать человек.
В этом случае можно рассуждать двояко либо кому-то правда не досталось места, либо же никто не говорил, какие именно пять человек пришли, но говориться, что три человека вернулись, то есть они могут быть в той пятерке, которая пришла.
Таким образом, для создания нового софизма нужно рассмотреть и понять уже известные нам. Но добиться чего-то совершенно нового очень и очень сложно.
Заключение.
Софизмы не новое понятие, пришедшее к нам от древнегреческих софистов. Ученные выделили ряд ошибок, на которых построенны софизмы.
Решение математических софизмов расширяет познание самой математики, ведь людой вид математических софизмов можно «решить» и зная ошибку ее не допустить в будущем.
Хотелось бы сказать пару слов о «создании» своего софизма.Во время работы над придумыванем софизма, мне было тяжело составить, что-то новое.
Занимаясь проектом, при решении задач на уроках я стала замечать места или случаи, где возможно было бы отклонится от правил. Не думаю, что те примеры можно считать за софизмы, ведь это просто ученические ошибки, но сама работа заставила меня видеть эти места.
Как выяснилось, малое количество людей знают, что такое софизм. Но старшие классы после объяснения лучше поняли принципы и смогли сами увидеть и указат ошибки (см. прил.).
Я считаю, что все мои цели и задачи, поставленные в начале работы, были достигнуты.
Приложение
Мне также было интересно, знают ли ученики разных возрастных категорий, что такое софизмы, и смогут ли они найти ошибки в математических, заведомо ложных, умозаключениях.
В рамках данного исследования ученикам 8 «Б» и 10 «В» классов (42 ученика) были предоставлены идентичные вопросники, включающие 3 вопроса:
1. Знакомо ли Вам понятие «софизм»? (Да/Нет)
2. Возьмём числовое равенство:
35+10-45=42+12-54.
Вынесем общие множители левой и правой частей за скобки.
Получим: 5(7+2-9)=6(7+2-9).
Разделим обе части этого равенства на общий множитель (заключенный в скобки).
Получаем 5=6.
Как Вы это объясните? (Ошибки нет/ Допущена ошибка в условии/ Допущена ошибка в решении (указать ошибку))
3. Дано уравнение x-a=0.
Разделив обе части этого уравнения на x-a, получим, что 1=0.
Поскольку это равенство неверное, то это означает, что исходное уравнение не имеет корней.
Допущена ли здесь ошибка, и если да, то какая? (Ошибки нет/ Допущена ошибка в условии/ Допущена ошибка в решении (указать ошибку))
Проанализировав ответы на вопросы, я получила следующие результаты:
1 вопрос: Знакомо ли Вам понятие «софизм»? (Да/Нет)
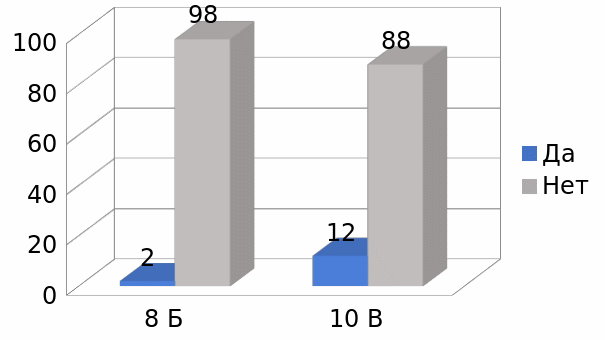
Из графика видно, что практически все ученики не знакомы с понятием софизма.
2 вопрос: Возьмём числовое равенство: 35+10-45=42+12-54.
Вынесем общие множители левой и правой частей за скобки. Получим: 5(7+2-9)=6(7+2-9).
Разделим обе части этого равенства на общий множитель (заключенный в скобки). Получаем 5=6.
Как Вы это объясните? (Ошибки нет/ Допущена ошибка в условии/ Допущена ошибка в решении (указать ошибку))
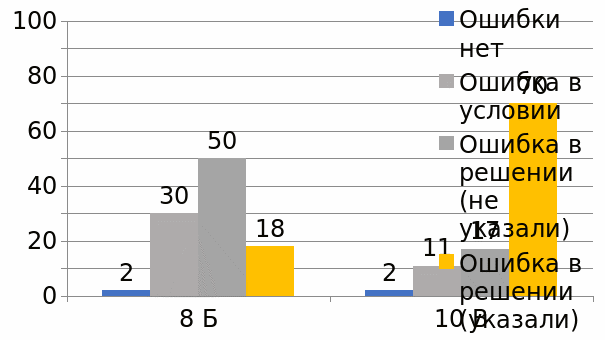
В этой задаче на внимательность нужно было найти конкретную математическую ошибку:7+2-9=0. На ноль делить нельзя.
С данной задачей справились 18% учеников 8 класса и 70%- 10 класса. При этом 50% восьмиклассников все же нашли наличие ошибки в решении, но не указали ее точно.
3 вопрос: Дано уравнение x-a=0.
Разделив обе части этого уравнения на x-a, получим, что 1=0.
Поскольку это равенство неверное, то это означает, что исходное уравнение не имеет корней.
Допущена ли здесь ошибка, и если да, то какая? (Ошибки нет/ Допущена ошибка в условии/ Допущена ошибка в решении (указать ошибку))
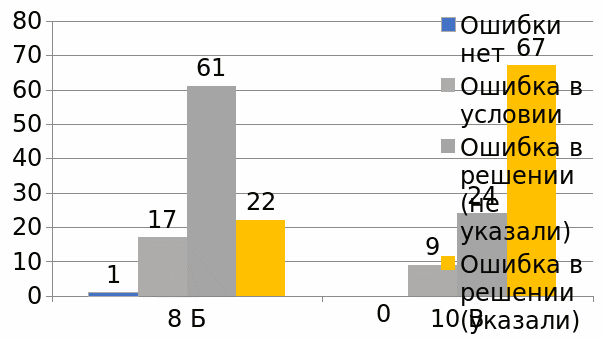
Ответом данной задачи было:
Поскольку x=a – корень уравнения, то, разделив на выражение x-a обе его части, мы потеряли этот корень и поэтому получили неверное равенство 1=0.Верно на этот вопрос ответили 22% 8-классников и 67% 10-классников, при этом наличие ошибки отметили 100% учеников обоих классов, то есть явление софизма определили все!
Список литературы:
Игнатьев Е.И. Математическая смекалка. Занимательные задачи, игры фокусы, парадоксы – М., «Омега», 1994;
Нагибин Ф.Ф.,Канин Е.С. Математическая шкатулка: Пособие для учащихся 4 – 8 кл. сред. Шк. – 5-е изд.–М.: Издательство «Просвещение», 1988;
Львовский С.М. Что не так? Математические парадоксы и софизмы. – М.: МЦИМО, 2019;
Мадера А.Г. Математические софизмы: Правдоподобные рассуждения, приводящие к ошибочным утверждениям: Кн. для учащихся 7 – 11 кл. /А.Г.Мадера,Д.А. Мадера – М., Просвещение, 2003;
Обреимов В.Н.Математические софизмы - С.-Петербург Типография Ю.Н.Эрлик, Седовая, №9 1989.
1�Львовский С.М. Что не так? Математические парадоксы и софизмы. – М.: МЦИМО, 2019; Обреимов В.Н. «Математические софизмы» - С.-Птербург Типография Ю.Н.Эрлик, Седовая, №9 1989; Мадера А.Г. Математические софизмы: Правдоподобные рассуждения, приводящие к ошибочным утверждениям: Кн. для учащихся 7 – 11 кл. / А.Г. Мадера, Д.А. Мадера – М., Просвещение, 2003
2�Нагибин Ф.Ф., Канин Е.С. Математическая шкатулка: Пособие для учащихся 4 – 8 кл. сред. Шк. – 5-е изд. – М.: Издательство «Просвещение», 1988.
3�Мадера А.Г. Математические софизмы: Правдоподобные рассуждения, приводящие к ошибочным утверждениям: Кн. для учащихся 7 – 11 кл. / А.Г. Мадера, Д.А. Мадера – М., Просвещение, 2003.
4�proza.ru
5�Нагибин Ф.Ф., Канин Е.С. Математическая шкатулка: Пособие для учащихся 4 – 8 кл. сред. Шк. – 5-е изд. – М.: Издательство «Просвещение», 1988.
6�Львовский С.М. Что не так? Математические парадоксы и софизмы. – М.: МЦИМО, 2019
7�Мадера А.Г. Математические софизмы: Правдоподобные рассуждения, приводящие к ошибочным утверждениям: Кн. для учащихся 7 – 11 кл. / А.Г. Мадера, Д.А. Мадера – М., Просвещение, 2003
8�Обреимов В.Н. Математические софизмы - С.-Петербург Типография Ю.Н.Эрлик, Седовая, №9 1989
9�Обреимов В.Н. Математические софизмы - С.-Петербург Типография Ю.Н.Эрлик, Седовая, №9 1989







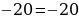
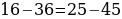
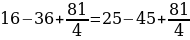
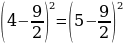
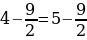
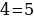
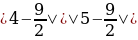
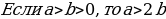
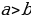 (натуральные числа)
(натуральные числа)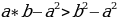
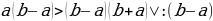
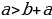
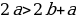
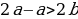
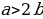
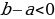 . При делении неравенства на отрицательное число, знак неравенства надо поменять, чего не было сделано.
. При делении неравенства на отрицательное число, знак неравенства надо поменять, чего не было сделано.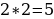
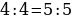
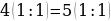
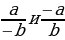 они равны, так как каждое из них равно
они равны, так как каждое из них равно 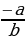 .Можно составить пропорцию:
.Можно составить пропорцию: 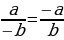 . Но если в пропорции предыдущий член первого отношения больше последующего, то предыдущий член второго отношения также больше своего последующего. В нашем случае
. Но если в пропорции предыдущий член первого отношения больше последующего, то предыдущий член второго отношения также больше своего последующего. В нашем случае 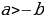 ; следовательно, должно быть
; следовательно, должно быть 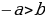 , т.е. отрицательное число больше положительного.
, т.е. отрицательное число больше положительного.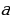 – какое угодно число. Возьмем тождество
– какое угодно число. Возьмем тождество 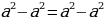 . В левой части его вынесем
. В левой части его вынесем 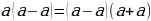 . Упростив это тождество, получим:
. Упростив это тождество, получим: 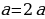 .
.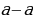 , т.к. это выражение будет равно нулю.
, т.к. это выражение будет равно нулю.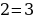
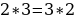
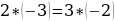
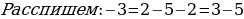
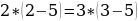
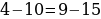
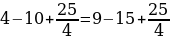
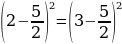
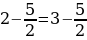
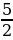 :
: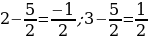 .Значит, в этом случае, если мы прибавим равные величины, то получим разные суммы.
.Значит, в этом случае, если мы прибавим равные величины, то получим разные суммы.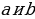 , гипотенузой
, гипотенузой 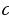
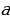 , противолежащим катету
, противолежащим катету 
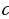
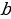

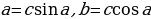 , откуда
, откуда 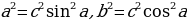 .
.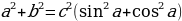 ,
,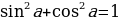 , и поэтому
, и поэтому 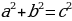 .
.
 рис.1
рис.1

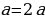 , нарушая правила, ведь делить на неизвестное нельзя, но эта ошибка работает только в буквенном виде. Получим:
, нарушая правила, ведь делить на неизвестное нельзя, но эта ошибка работает только в буквенном виде. Получим: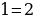 , и мы создали новый софизм. Правда, это не совсем новый софизм. Давайте подставим в софизм число 3:
, и мы создали новый софизм. Правда, это не совсем новый софизм. Давайте подставим в софизм число 3: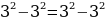
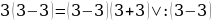
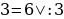
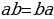















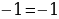
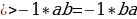
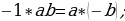
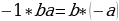
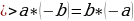
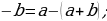
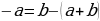
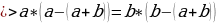
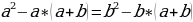
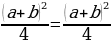
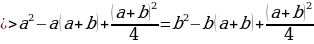
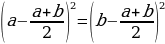
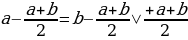
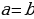
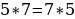
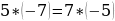
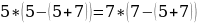
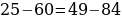
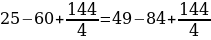
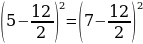
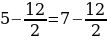
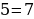
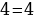
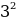 :
: