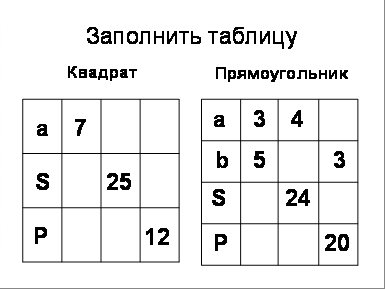
| Теоретический материал § 21
Площади каких фигур вы уже умеете вычислять?
– Что показывает площадь? (Сколько места занимает фигура на плоскости) - у вас на партах разные фигуры, сравните их, выберите самую большую, самую маленькую. Как измерить площадь фигуры? Сначала нужно выбрать единицу площади, т.е. указать единичный квадрат, т.е. квадрат, сторона которого служит единицей длины. При выбранной единице измерения площадей площадь каждого многоугольника показывает сколько раз единица измерения и ее части укладываются в данном многоугольнике. - у вас на партах в конвертах различные единицы измерения площади- квадраты, со стороной 1 см, 1 дм. Какую единицу вы выберите, чтобы найти площадь вашего прямоугольника? Работая в парах, найдите площадь фигуры 1. (Ученики укладывают квадраты, со стороной 1 см. в фигуре, сообщают учителю количество) Мы нашли площадь нашей фигуры. Запишем S = … см2 А чтобы найти площадь моей фигуры, квадрат с какой стороной нужно выбрать? (Учитель показывает большую фигуру) К доске выходят несколько учеников, выбирают квадраты, укладывают на фигуре, сообщают площадь. Чтобы найти площадь класса, квадрат с какой стороной нужно выбрать? Удобно ли пользоваться теми, что есть у нас? 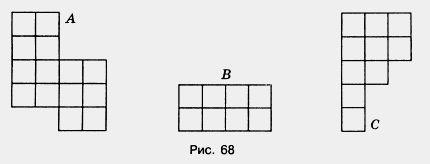
Найдите площадь каждой фигуры, изображенной на рисунке 68, если условиться, что длина стороны каждой клетки равна 1 см. Итак, чтобы найти площадь фигуры, нужно: 1. Выбрать единицу измерения, посчитать, сколько раз эта единица укладывается в данной фигуре. Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников. Это свойство площади многоугольника. Равные многоугольники имеют равные площади. Найдите площадь прямоугольника, который есть у вас. Удобно ли каждый раз укладывать единичные квадраты в наших фигурах? Предложите способ, который позволяет вычислить площадь прямоугольника, не используя способ подсчета уместившихся квадратов. S = a * b А как называется прямоугольник, у которого длина и ширина равны? (Квадрат) Он давно знакомый мой. Каждый угол в нем прямой, Все четыре стороны одинаковой длины. Вам его представить рад, А зовут его …(квадрат). Как найти его площадь? S = a∙a = a2 А периметр? Р = а + а + а + а = 4а
|