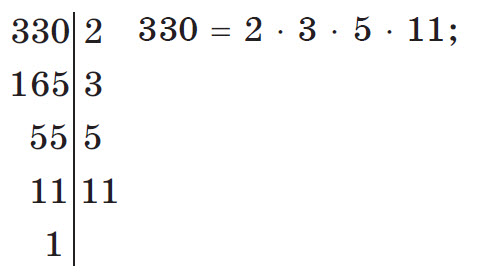Математика. Делимость и простые числа.

Делимость — одно из основных понятий арифметики и теории чисел, связанное с операцией деления. С точки зрения теории множеств, делимость целых чиселявляется отношением, определённым на множестве целых чисел. Если для некоторого целого числа.

Делителем натурального числа а называется натуральное число, на которое а делится без остатка. Число 1 является делителем любого натурального числа.

Натуральное число называется простым, если оно имеет только два делителя: единицу и само это число. Например, числа 2, 3, 11, 23 — простые числа.

Число, имеющее более двух делителей, называется составным. Например, числа 4, 8, 15, 27 — составные числа.

Признак делимости произведения нескольких чисел: если хотя бы один из множителей делится на некоторое число, то и произведение делится на это число. Произведение 24 • 15 • 77 делится на 12, поскольку множитель этого числа 24 делится на 12.

Признак делимости суммы (разности) чисел: если каждое слагаемое делится на некоторое число, то и вся сумма делится на это число. Если а : b и c : b, то (а + c) : b. А если а : b, а c не делится на b, то a + c не делится на число b.

Если а : c и c : b, то а : b. Исходя из того, что 72:24 и 24:12, делаем вывод, что 72:12.

Представление числа в виде произведения степеней простых чисел называют разложением числа на простые множители.

Основная теорема арифметики: любое натуральное число (кроме 1) либо является простым, либо его можно разложить на простые множители только одним способом.

При разложении числа на простые множители используют признаки делимости и применяют запись «столбиком» В таком случае делитель располагается справа от вертикальной черты, а частное записывают под делимым.

Например, задание: разложить на простые множители число 330. Решение:

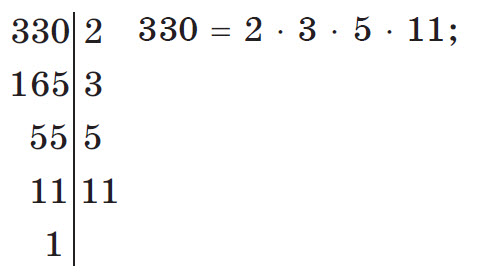
Признаки делимости  на  2,  5,  3,  9,  10,  4,  25  и  11.

Существуют признаки делимости на 6, 15, 45 и т. д., то есть на числа, произведение которых можно разложить на множители 2, 3, 5, 9 и 10.

Наибольший общий делитель 

Наибольшее натуральное число, на которое делится нацело каждое из двух данных натуральных чисел, называется наибольшим общим делителемэтих чисел (НОД).   Например, НОД (10; 25) = 5;   а НОД (18; 24) = 6;    НОД (7; 21) = 1.

Если наибольший общий делитель двух натуральных чисел равен 1, то эти числа называются взаимно простыми.

Алгоритм нахождения наибольшего общего делителя (НОД)