Математика. Диагностическая контрольная работа для 8 класса

Административная контрольная работа по математике в 8 классе

I вариант.

Часть 1.

При выполнении заданий первой части ответы укажите сначала на листах с заданиями, а затем перенесите в бланк № 1. Все необходимые вычисления, преобразования выполняйте в черновике.

1. Запишите в ответе номера верных равенств.

1) 2) 3) .

Ответ: __________________.

2. Найдите значение выражения (2^{- 4})² ∙ 2¹⁰.

Ответ: ____________________.

3. Для приготовления фарша взяли говядину и свинину в отношении

7 : 13. Какой процент в фарше составляет говядина?

Ответ: ____________________.

4. Укажите номер верного утверждения:

1) a³ 0 2) a – b 0 3) ab a + b 1.

5. Решите уравнение х² – 7х = 0.

В ответ запишите корни, если корней несколько, разделяйте корни точкой с запятой.

Ответ: ____________________.

6. На тренировке в 50 – метровом бассейне пловец проплыл 200 – метровую дистанцию. На рисунке изображён график зависимости расстояния между пловцом и точкой старта от времени движения пловца. Определите, на каком отрезке дистанции скорость пловца была наибольшей.

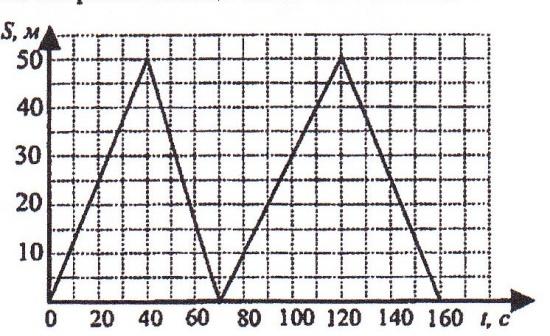
1) 0 м – 50 м 2) 50 м – 100 м

3) 100 м – 150 м 4) 150 м – 200 м.

7. Наклонная крыша установлена в трёх вертикальных опорах, расположенных на одной прямой. Средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота малой опоры

1,8 м, высота большой опоры 2,8 м. Найдите высоту средней опоры.

Ответ: ________________.

8. Упростите выражение: .

1) 2) 3) 6 4)

9. Решите неравенство 3(6 – х) ≥ 2 – х.

Ответ: _______________.

10. Найдите ∟С, если ∟А = 62˚.

Ответ: _________________.

11. Найдите значение выражения: .

1) 1200 2) 12 3) 120 4) 36

12. Укажите в ответе номера верных утверждений.

1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.

2) Если две стороны и угол одного треугольника соответственно равны двум сторонам и углу другого треугольника, то такие треугольники равны.

3) Косинусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

4) Если в ромбе один из углов равен 90˚, то такой ромб – квадрат.

Ответ: _______________.

13. Из равенства выразите переменную v (все величины положительны).

Ответ: ________________.

14. Мотоциклист проехал 40 км от дома до реки. Возвращаясь обратно со скоростью на 10 км/ч меньшей первоначальной, он затратил на этот путь на 20 минут больше. Найдите первоначальную скорость мотоциклиста.

Если эту скорость обозначить за х км/ч, то задача может быть решена с помощью уравнения:

1) 2)

3) 4) х + 3(х – 10) = 40.

Часть II.

Для ответов на задания 15 – 17 используйте бланк № 2. укажите сначала номер задания, а затем запишите его решение.

15. (2 балла) Решите уравнение:

16. (2 балла) Найдите область определения функции

у = .

17. (3 балла) На сторонах АС и АВ треугольника АВС отмечены соответственно точки В₁ и С₁. Известно, что АВ₁ = 3 см, В₁С = 17 см, АС₁ = 5 см, С₁В = 7см. Докажите, что треугольники АВС и АВ₁С₁ подобны.

Административная контрольная работа по математике в 8 классе

II вариант.

Часть 1.

При выполнении заданий первой части ответы укажите сначала на листах с заданиями, а затем перенесите в бланк № 1. Все необходимые вычисления, преобразования выполняйте в черновике.

1. Запишите в ответе номера верных равенств.

1) 2) 3) .

Ответ: __________________.

2. Найдите значение выражения (7 ⁴)^-2 ∙ 7¹⁰.

Ответ: ____________________.

3. Для фруктового напитка смешивают яблочный и виноградный сок в отношении 13 : 7. Какой процент в этом напитке составляет виноградный сок?

Ответ: ____________________.

4. Укажите номер верного утверждения:

1) a + b 0 2) 3) ab a – b)c

5. Решите уравнение х² – 16 = 0.

В ответ запишите корни, если корней несколько, разделяйте корни точкой с запятой.

Ответ: ____________________.

6. На тренировке в 50 – метровом бассейне пловец проплыл 200 – метровую дистанцию. На рисунке изображён график зависимости расстояния между пловцом и точкой старта от времени движения пловца. Определите, на каком отрезке дистанции скорость пловца была наибольшей.

1) 0 м – 50 м 2) 50 м – 100 м

3) 100 м – 150 м 4) 150 м – 200 м.

7. Наклонная крыша установлена в трёх вертикальных опорах, расположенных на одной прямой. Средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота малой опоры

1,7 м, высота средней опоры 2,1 м. Найдите высоту большей опоры.

Ответ: ________________.

8. Упростите выражение: .

1) 2) 3) 4) 4

9. Решите неравенство 9(2 – х) ≤ 4 – 7х.

Ответ: _______________.

10. Найдите ∟А, если ∟С = 32˚.

Ответ: _________________.

11. Найдите значение выражения: .

1) 280 2) 2800 3) 28 4) 700

12. Укажите в ответе номера верных утверждений.

1) Существуют три прямые, которые проходят через одну точку.

2) Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.

3) Синусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.

4) Если в прямоугольнике диагонали перпендикулярны, то такой прямоугольник – квадрат.

Ответ: _______________.

13. Из равенства выразите переменную r (все величины положительны).

Ответ: ________________.

14. Товарный поезд был задержан в пути на 18 минут, а затем на расстоянии в 60 км наверстал это время, увеличив скорость на 10 км/ч. Найдите первоначальную скорость поезда.

Если принять первоначальную скорость поезда за х км/ч, то задача будет решаться с помощью уравнения:

1) 2)

3) 4)

Часть II.

Для ответов на задания 15 – 17 используйте бланк № 2. укажите сначала номер задания, а затем запишите его решение.

15. (2 балла) Решите уравнение:

16. (2 балла) Найдите область определения функции

у = .

17. (3 балла) На сторонах АС и АВ треугольника АВС отмечены соответственно точки В₁ и С₁. Известно, что АВ₁ = 4 см, В₁С = 17 см, АС₁ = 7 см, С₁В = 5см. Докажите, что треугольники АВС и АВ₁С₁ подобны.

Часть 1.

При выполнении заданий первой части ответы укажите сначала на листах с заданиями, а затем перенесите в бланк № 1. Все необходимые вычисления, преобразования выполняйте в черновике.

1. Запишите в ответе номера верных равенств.

1) 2) 3) .

Ответ: __________________.

2. Найдите значение выражения 5⁸ ∙ (5^-3)².

Ответ: ____________________.

3. Для приготовления чайной смеси смешивают индийский и цейлонский чай в отношении 9 : 11. Какой процент в этой смеси составляет цейлонский чай?

Ответ: ____________________.

4. Укажите номер верного утверждения:

1) b – a a² – b² 4) a + b

5. Решите уравнение 5х² – 3х = 0.

В ответ запишите корни, если корней несколько, разделяйте корни точкой с запятой.

Ответ: ____________________.

6. На тренировке в 25 – метровом бассейне пловец проплыл 100 – метровую дистанцию. На рисунке изображён график зависимости расстояния между пловцом и точкой старта от времени движения пловца. Определите, на каком отрезке дистанции скорость пловца была наименьшей.

1) 0 м – 25 м 2) 25 м – 50 м

3) 50 м – 75 м 4) 75 м – 100 м.

7. Наклонная крыша установлена в трёх вертикальных опорах, расположенных на одной прямой. Средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота средней опоры

2,2 м, высота большей опоры 2,5 м. Найдите высоту меньшей опоры.

Ответ: ________________.

8. Упростите выражение: .

1) 2) - 4а 3) 4)

9. Решите неравенство 6(2 – х) + 8 ≤ - х.

Ответ: _______________.

10. Найдите ∟С, если АВ = ВС.

Ответ: _________________.

11. Найдите значение выражения: .

1) 2000 2) 200 3) 20 4) 2

12. Укажите в ответе номера верных утверждений.

1) Если при пересечении двух прямых третьей прямой образовавшиеся внутренние односторонние углы равны, то такие две прямые параллельны.

2) Отношение площадей подобных треугольников равно коэффициенту подобия.

3) Тангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему катету.

4) Если в параллелограмме две соседние стороны равны, то такой параллелограмм является ромбом.

Ответ: _______________.

13. Из равенства выразите переменную I (все величины положительны).

Ответ: ________________.

14. Плот проплывает по течению 60 км на 5 ч быстрее, чем такое же расстояние проходит моторная лодка против течения. Найдите скорость лодки по течению, если её скорость в стоячей воде 10 км/ч.

Обозначив скорость течения за х км/ч, можно составить уравнение:

1) 2)

3) 4)

Часть II.

Для ответов на задания 15 – 17 используйте бланк № 2. укажите сначала номер задания, а затем запишите его решение.

15.(2 балла) Решите уравнение:

16. (2 балла) Найдите область определения функции

у =.

17. (3 балла) На сторонах АС и АВ треугольника АВС отмечены соответственно точки В₁ и С₁. Известно, что АВ₁ = 12 см, В₁С = 3 см, АС₁ = 10 см, С₁В = 8 см. Докажите, что треугольники АВС и АВ₁С₁ подобны.

18. (3 балла)  Пер­вый ра­бо­чий за час де­ла­ет на 5 де­та­лей боль­ше, чем вто­рой, и вы­пол­ня­ет заказ, со­сто­я­щий из 200 де­та­лей, на 2 часа быст­рее, чем вто­рой ра­бо­чий, вы­пол­ня­ю­щий такой же заказ. Сколь­ко де­та­лей в час де­ла­ет вто­рой ра­бо­чий?

24. За­да­ние 24 № 311249. Ос­но­ва­ния рав­но­бед­рен­ной тра­пе­ции равны 8 и 18, а пе­ри­метр равен 56.

Най­ди­те пло­щадь тра­пе­ции.

Ре­ше­ние.

Тра­пе­ция рав­но­бед­рен­ная, зна­чит,

 

 и 

Тогда,

 

Ответ: 

24. За­да­ние 24 № 314950. Сто­ро­на ромба равна 20, а ост­рый угол равен 60° . Вы­со­та ромба, опу­щен­ная из вер­ши­ны ту­по­го угла, делит сто­ро­ну на два от­рез­ка. Ка­ко­вы длины этих от­рез­ков?

Ре­ше­ние.

Введём обо­зна­че­ния, как по­ка­за­но на ри­сун­ке. Тре­уголь­ник ABH — пря­мо­уголь­ный, в нём угол A равен 60°. Тогда от­ре­зок AH можно найти по фор­му­ле:

 

 

Найдём от­ре­зок HD

Ответ: 10,10.

18. вариант 2  Рас­сто­я­ние между при­ста­ня­ми А и В равно 140 км. Из А в В по те­че­нию реки от­пра­вил­ся плот, а через час вслед за ним от­пра­ви­лась мо­тор­ная лодка, ко­то­рая, при­быв в пункт В, тот­час по­вер­ну­ла об­рат­но и воз­вра­ти­лась в А. К этому вре­ме­ни плот прошёл 51 км. Най­ди­те ско­рость лодки в не­по­движ­ной воде, если ско­рость те­че­ния реки равна 3 км/ч.

Ре­ше­ние.

Плот прошёл 51 км, зна­чит, он плыл 17 часов, из ко­то­рых лодка на­хо­ди­лась в пути 16 часов. Пусть ско­рость лодки в не­по­движ­ной воде равна v км/ч, тогда

 

 

от­ку­да v = 18. Ответ: 18 км/ч.

18. вариант 1 Пер­вый ра­бо­чий за час де­ла­ет на 5 де­та­лей боль­ше, чем вто­рой, и вы­пол­ня­ет заказ, со­сто­я­щий из 200 де­та­лей, на 2 часа быст­рее, чем вто­рой ра­бо­чий, вы­пол­ня­ю­щий такой же заказ. Сколь­ко де­та­лей в час де­ла­ет вто­рой ра­бо­чий?

Ре­ше­ние.

Пусть вто­рой ра­бо­чий де­ла­ет за час х де­та­лей, тогда пер­вый ра­бо­чий де­ла­ет за час х + 5 де­та­лей. По­лу­ча­ем урав­не­ние:

 

 

от­ку­да х = 20. Ответ: 20.

3 вариант№18 . Пер­вый ра­бо­чий за час де­ла­ет на 5 де­та­лей боль­ше, чем вто­рой, и вы­пол­ня­ет заказ, со­сто­я­щий из 180 де­та­лей, на 3 часа быст­рее, чем вто­рой ра­бо­чий, вы­пол­ня­ю­щий такой же заказ. Сколь­ко де­та­лей в час де­ла­ет вто­рой ра­бо­чий?

Ре­ше­ние.

Пусть вто­рой ра­бо­чий де­ла­ет за час x де­та­лей, тогда пер­вый ра­бо­чий де­ла­ет за час x + 5 де­та­лей. По­лу­ча­ем урав­не­ние:

 

 

от­ку­да x = 15. Ответ: 15.