Первой работой теории графов как математической дисциплины считают статью Эйлера (1736 г.), в которой рассматривалась задача о Кёнингсбергских мостах. Эйлер показал, что нельзя обойти семь городских мостов и вернуться в исходную точку, пройдя по каждому мосту ровно один раз. Следующий импульс теория графов получила спустя почти 100 лет с развитием исследований по электрическим сетям, кристаллографии, органической химии и другим наукам.
С графами, сами того не замечая, мы сталкиваемся постоянно. Например, графом является схема линий метрополитена. Точками на ней представлены станции, а линиями — пути движения поездов. Исследуя свою родословную и возводя ее к далекому предку, мы строим так называемое генеалогическое древо. И это древо — граф.
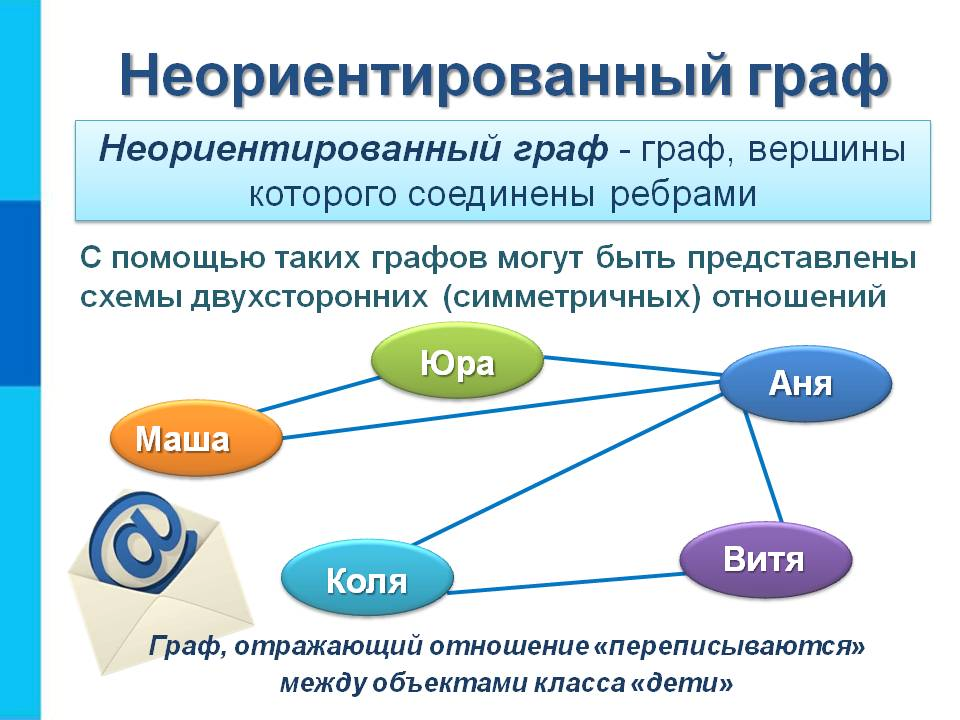
Графы служат удобным средством описания связей между объектами. Ранее мы уже использовали графы как способ наглядного представления конечных бинарных отношений. Но граф используют отнюдь не только как иллюстрацию. Например, рассматривая граф, изображающий сеть дорог между населенными пунктами, можно определить маршрут проезда от пункта А до пункта Б. Если таких маршрутов окажется несколько, хотелось бы выбрать в определенном смысле оптимальный, например самый короткий или самый безопасный. Для решения задачи выбора требуется проводить определенные вычисления над графами. При решении подобных задач удобно использовать алгебраическую технику, да и само понятие графа необходимо формализовать.
Методы теории графов широко применяются в дискретной математике. Без них невозможно обойтись при анализе и синтезе различных дискретных преобразователей: функциональных блоков компьютеров, комплексов программ и т.д.
Неориентированные графы

Неориентированный граф G задается двумя множествами G=(V,E)G=(V,E), где V — конечное множество, элементы которого называют вершинами или узлами; EE — множество неупорядоченных пар на VV, т.е. подмножество множества двухэлементных подмножеств VV, элементы которого называют ребрами. Для каждого ребра {u,v}∈E{u,v}∈E считаем, что uu и vv— различные вершины.
Если ребро e={u,v}e={u,v}, то говорят, что ребро ee соединяет вершины uu и vv, и обозначают это мы u↦vu↦v; если необходимо, указывают имя графа G:u↦GvG:u↦Gv.
Вершины uu и vv, соединенные ребром (u↦v)(u↦v), называют смежными, а также концами ребра {u,v}{u,v}. Если u↦vu↦v, говорят, что вершины uu и vv связаны отношением непосредственной достижимости.
Ребро ee называют инцидентным вершине vv, если она является одним из его концов.
Степенью вершины vv называют число dgvdgv всех инцидентных ей ребер.
Для вершины vv множество Γ(v)={x:x↦v}Γ(v)={x:x↦v} называют множеством смежных с vvвершин. Справедливо равенство dgv=|Γ(v)|dgv=|Γ(v)|.
Цепь в неориентированном графе GG — это последовательность вершин (конечная или бесконечная) v0,v1,…,vn,…v0,v1,…,vn,…, такая, что vi↦vi+1vi↦vi+1 для любого ii, если vi+1vi+1существует. (Под конечной последовательностью понимается кортеж вершин.)
Для конечной цепи v0,v1,…,vnv0,v1,…,vn число n (n⩾0)n (n⩾0) называют длиной цепи. Таким образом, длина цепи есть число ее ребер, т.е. всех ребер, соединяющих вершины vivi и vi+1 (i=0,n−1¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯)vi+1 (i=0,n−1¯). Цепь длины 0 — это произвольная вершина графа.
Говорят, что вершина vv неориентированного графа GG достижима из вершины uu этого графа и обозначают и u∣=∣∗vu∣=∣∗v, если существует цепь v0,v1,…,vnv0,v1,…,vn такая, что u=v0,u=v0, vn=vvn=v (при этом говорят также, что данная цепь соединяет вершины uu и vv, которые называют концами цепи). Таким образом, задано отношение достижимости ∣=∣∗∣=∣∗ в неориентированном графе. Оно является рефлексивно-транзитивным замыканием отношения ∣−∣∣−∣непосредственной достижимости.
Отношение достижимости в неориентированном графе рефлексивно, симметрично и транзитивно, т.е. является отношением эквивалентности
Если существует цепь ненулевой длины, соединяющая uu и vv, то пишут u∣=∣+vu∣=∣+v. Если необходимо явно указать длину цепи, то пишут u∣=∣nvu∣=∣nv и говорят, что существует цепь длины nn, соединяющая uu и vv.
Простая цепь — это цепь, все вершины которой, кроме, быть может, первой и последней, попарно различны и все ребра попарно различны.
Простую цепь ненулевой длины с совпадающими концами называют циклом.
Произвольную цепь ненулевой длины с совпадающими концами, все ребра которой попарно различны, будем называть замкнутой цепью.
Неориентированный граф, не содержащий циклов, называют ациклическим графом.
Просмотр содержимого документа
«Математика. Графы. Определение неориентированного графа.»
Графы. Определение неориентированного графа.
Граф - это двойка , где V - непустое множество вершин, а Е - множество ребер, соединяющих эти вершины попарно.
Две вершины, связанные между собой ребром, равноправны, и именно поэтому такие графы называются неориентированными: нет никакой разницы между "началом" и "концом" ребра.
Говоря простым языком, граф - это множество точек (для удобства изображения - на плоскости) и попарно соединяющих их линий (не обязательно прямых). В графе важен только факт наличия связи между двумя вершинами. От способа изображения этой связи структура графа не зависит.
| Таблица 1. Примеры неориентированных графов
|
| Граф | Вершины | Ребра |
| Семья | Люди | Родственные связи |
| Город | Перекрестки | Улицы |
| Сеть | Компьютеры | Кабели |
| Домино | Костяшки | Возможность |
| Дом | Квартиры | Соседство |
| Лабиринт | Развилки и тупики | Переходы |
| Метро | Станции | Пересадки |
| Листок в клеточку | Клеточки | Наличие общей границы |
Рассмотрим конечное Непустое множество  мощности
мощности  и множество
и множество  мощности
мощности  двухэлементных подмножеств множества
двухэлементных подмножеств множества  .
.
Определение. Неориентированным графом  , или
, или  , называется пара множеств
, называется пара множеств  и
и  .
.
Элементы множества  называются Вершинами Графа
называются Вершинами Графа  , элементы множества
, элементы множества  – его Ребрами. Ребро, соединяющее две различные вершины графа
– его Ребрами. Ребро, соединяющее две различные вершины графа  или, что то же самое,
или, что то же самое,  , обозначается
, обозначается  .
.
Ребра графа нумеруются Вне Зависимости от номеров соединяемых вершин. Указание множества вершин и множества ребер является Аналитическим способом задания графа.
Теорема.1. Любое множество  двухэлементных подмножеств множества
двухэлементных подмножеств множества  является симметричным бинарным отношением на множестве
является симметричным бинарным отношением на множестве  .
.
В силу теоремы 1 для множества  выполняются свойства:
выполняются свойства:  и
и  . Поэтому всякий элемент
. Поэтому всякий элемент  обозначается
обозначается  или, что то же самое,
или, что то же самое,  . Таким символом в теории графов обозначается двухэлементное множество .
. Таким символом в теории графов обозначается двухэлементное множество .
Списком ребер графа называется перечень его ребер с указанием соединяемых вершин.
Определение. Инцидентной ребру называется каждая из концевых вершин этого ребра. Ребро называется инцидентным своим концевым вершинам.
Определение. Смежными называются два ребра, инцидентные одной вершине.
Определение. Смежными называются две вершины, инцидентные одному ребру.
Определение. Диаграммой называется изображение графа в виде точек и линий.
Диаграмма является Геометрическим способом задания графа.
Например, на рис. 1 приведена диаграмма графа  , имеющего четыре вершины и пять ребер.
, имеющего четыре вершины и пять ребер.
Рис. 1. Диаграмма графа 
Множеством вершин графа является множество . Множеством ребер графа является множество с элементами , , , , .
В этом графе вершины  ,
,  ,
,  ,
,  ,
,  являются смежными; ребра
являются смежными; ребра  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  – смежными.
– смежными.
В этом графе вершины  являются несмежными, ребра
являются несмежными, ребра  ,
,  – несмежными.
– несмежными.
Определение. Подграфом графа  называется граф , для которого
называется граф , для которого  или
или  .
.
Факт, что является подграфом графа  , обозначается
, обозначается  .
.
Определение. Подграф называется Остовным подграфом  , если
, если  .
.
Определение. Подграф называется Собственным подграфом  , если
, если  и
и  .
.
Определение. Подграф называется Правильным подграфом  , если
, если  .
.
Например, на рис. 2 представлены диаграммы подграфов графа, изображенного на рис. 1.
А) Б) В)
Рис. 2. Диаграммы подграфов: А – остовной; Б – собственный; В – правильный
Определение. Петлей графа называется элемент множества E, состоящий из одинаковых элементов множества V.
Граф с петлей называется Псевдографом.
Определение. Кратными ребрами графа называется набор одинаковых элементов множества E.
Граф с кратными ребрами называется Мультиграфом.
Определение. Гиперграфом называется граф, для которого множество Е состоит из троек, четверок, …, P-ок элементов множества V.
Определение. Помеченным называется граф с дополнительно заданной функцией  или
или  . Множество М называется Множеством пометок.
. Множество М называется Множеством пометок.
Далее рассматриваются неориентированные непомеченные графы без петель и кратных ребер.
Допускается обозначение вершин на диаграмме графа натуральными числами от 1 до P или только точками.
Задачи и упражнения
1. Запишите множества V и E, определите числа P и Q, укажите все пары смежных вершин графов, заданных следующими диаграммами:
2. Задайте графы задачи 1 списком ребер. Укажите все пары смежных ребер.
3. Выделите остовной, собственный и правильный подграфы графов задачи 1.
4. Постройте диаграммы следующих графов, имеющих 5 вершин и заданных списками ребер:
1) , , , ;
2) , , , , , , , .
Тема: Графы. Определение неориентированного графа. Оформлена работа Хартон М. Страница 2



















