Математика. Промежутки знакопостоянства функции + примеры

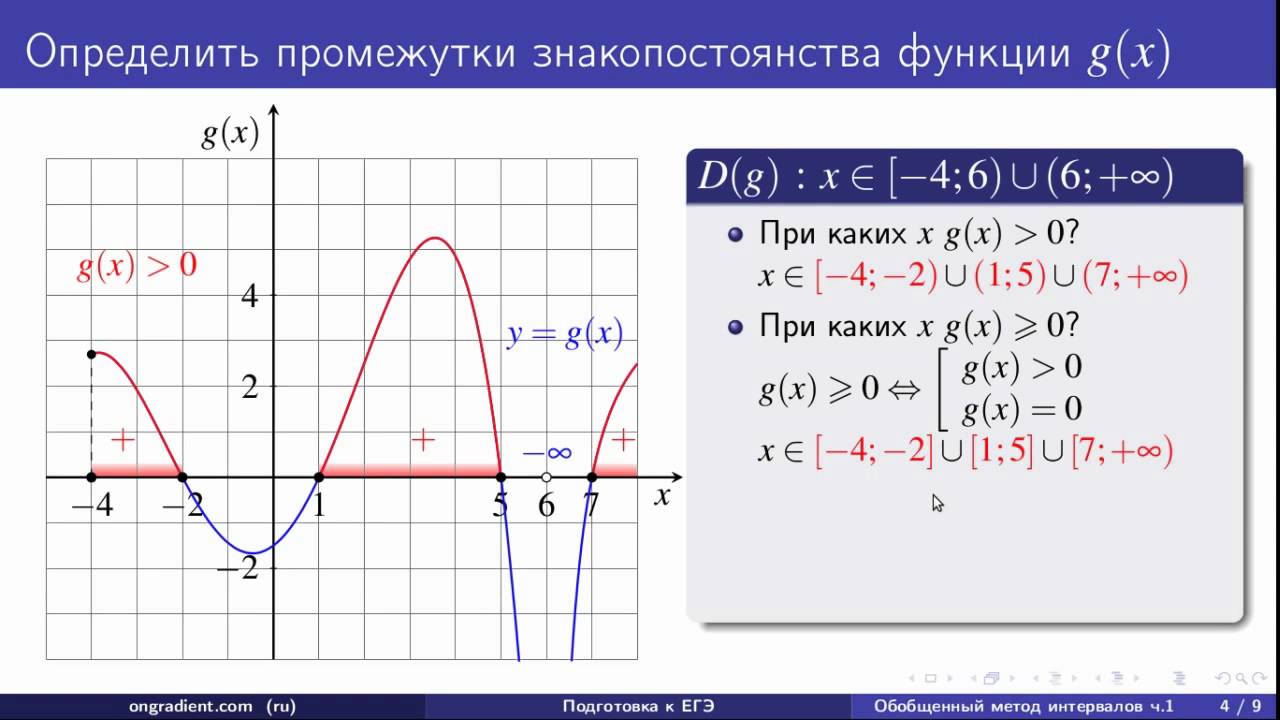
Промежутки знакопостоянства — такие промежутки на области определения, в которых значения функции сохраняют свой знак.

Для нахождения промежутков знакопостоянства функции y=f(x) надо решить неравенства f(x)>0, f(x)<0.

Пример: Найдем промежутки знакопостоянства функции y=x2+x−2. Решим неравенство: x2+x−2<0. Сначала найдем нули функции f(x)=x2+x−2:

x2+x−2=0 D=1−4⋅(−2)=9 x=−1±32 x1=1,x2=−2

Таким образом, получились промежутки значений аргумента, в которых функция сохраняет знак:

(−∞;−2),(−2;1),(1;+∞)

Для того, чтобы определить знак функции на каждом из этих промежутков, найдем значение функции в произвольной точке из каждого промежутка. Точки выбираются из соображений удобства вычислений.  Возьмем значения аргумента: −3∈(−∞;−2), 0∈(−2;1) и 2∈(1;+∞) и найдем для них значения функции. f(−3)=(−3)2+(−3)−2=9−3−2=4 f(0)=−2 f(2)=4

Значит, в промежутке (−∞;−2) функция принимает положительные значения, в промежутке (−2;1) — отрицательные и в промежутке (1;+∞) — положительные. Это же можно наблюдать на графике функции: