Россия, Северск
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 04.07.2017 10:58
Ласточкина Ольга Геннадьевна
Учитель математики
633
84 300 
Местоположение
Специализация
Математический марафон. Задачи и их решение
Категория:
Математика
24.04.2017 03:55
Просмотр содержимого документа
«Математический марафон. Задачи и их решение»
6 класс
Дорогие ребята!
Предлагаем вам задачи «Математического марафона
На доске написаны натуральные числа от 1 до 2010. Разрешается стереть любые два числа и вместо них записать их разность. Сколько раз нужно выполнить эту операцию, чтобы на доске осталось одно число? Какое это число – четное, или нечетное?
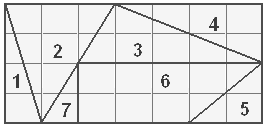
Пять Маленьких Поварят решили разделить между собой большую прямоугольную шоколадку. Но она упала на пол, и когда они развернули ее, то увидели, что шоколадка разбилась на 7 кусков. Николай съел самый большой кусок. Света и Маша съели одно и тоже количество шоколада, но Света съела три куска, а Маша только один кусок. Белла съела 1/7 часть целой шоколадки, и Катя съела все остальное. Какой кусок шоколадки достался Кате?
Из поврежденной книги выпала часть сшитых вместе листов. Номер первой выпавшей страницы – 143. Номер последней записан теми же цифрами, но в ином порядке. Сколько страниц выпало из книги?
Ужасный вирус пожирает память компьютера. За первую секунду он управился с половиной памяти, за вторую секунду-с одной третью оставшейся части, за третью секунды-с четвертью того, что еще сохранилось, за четвертую-с одной пятой остатка. И тут настиг его могучий Антивирус. Какая часть памяти удалена?
Как расположить на плоскости 9 отрезков, чтобы каждый имел общие точки ровно с четырьмя другими?
Если в числовой автомат ввести какое-то число, то он может за один шаг прибавить к нему 2 или 3 или умножить его на 2 или на 3. В автомат ввели число 1 и заставили его перебрать все возможные комбинации из трех ходов. Сколько раз при этом в результате получились четные числа?
Имеется 6 палочек, длины которых равны 1см, 2см, 3см, 2008см, 2009см, 2010см. Надо выбрать три палочки и составить из них треугольник. Каким числом способов можно подобрать подходящие тройки палочек?
Старший брат идет от дома до школы 12 мин, а младший брат – 16 мин. Сколько минут потребуется старшему брату, чтобы догнать младшего, который вышел на одну минуту раньше?
Решение
математического марафона
6 класс
№1.
Ответ: 2009 раз нужно выполнить операцию. Нечетное число останется.
Всего 2010 чисел.
Уберем любые два числа и вместо них запишем их разность. Чисел стало 2009.
Уберем еще любые два числа и вместо них запишем их разность. Чисел стало 2008.
Если эти действия повторять далее, то чисел каждый раз становится на одно меньше.
Заметим: 1 действие - 2009 чисел,
2 действие - 2008 чисел,
3 действие - 2007 чисел,
…………………………,
2008 действие -2 числа,
2009 действие - 1 число.
Вывод: 2009 раз нужно выполнить эту операцию, чтобы на доске осталось одно число
1,2,3,4,5,6,7,,8.9,10,…,2009, 2010. Всего 2010 чисел.
1005 пар чисел или 1005 действий, каждое из которых равно 1:
1 действие: 2-1=1,
2 действие: 4-3=1,
3 действие: 5-4=1,
4 действие: 7-6=1.
………………………………,
1005 действие: 2010-2009=1,
из результата 2-го действия вычесть результат 3-го действия, то есть 1-1=0,
из результата 4-го действия вычесть результат 5-го действия, то есть 1-1=0,
……………………………………………………………………………………………,
из результата 1005-го действия вычесть результат 1004-го действия, то есть 1-1=0
Продолжим выполнение действий далее: вычитаем 0 из 0, заменяем 0 и т.д. Получим в результате ноль.
из результата 1-го действия вычесть результат последнего действия, то есть 1-0=1
Вывод: 1 - нечетное число
Ответ: 2009 раз нужно выполнить операцию; нечетное число останется.
№2.
Ответ: 2-й кусочек шоколадки достался Кате.
Посчитаем площадь каждого кусочка шоколада. Треугольник достраиваем до прямоугольника. Находим площадь прямоугольника: умножаем ширину на длину. Площадь треугольника равна половине площади прямоугольника, так как диагональ прямоугольника делит его на два равных треугольника, площади, которых тоже равны Получим:
| № кусочка шоколада | Площадь шоколада | Кто съел шоколад | Условие задачи |
| 1 | 2 кв.ед. | Света | первый кусочек |
| 2 | 6 кв.ед. | Катя | остальное |
| 3 | 5 кв.ед. | Маша | 1 кусочек |
| 4 | 4 кв.ед. | Белла | 1/7 часть всего шоколада |
| 5 | 2 кв.ед. | Света | второй кусочек |
| 6 | 8 кв.ед. | Николай | самый большой |
| 7 | 1 кв.ед. | Света | третий кусочек |
Ответ: Второй кусочек шоколада съела Катя.
№3.
Ответ: 172 страницы выпало из книги
Из поврежденной книги выпала часть сшитых вместе листов. Так первая страница 143- нечетная, то последняя страница всегда будет четной. По условию задачи номером последней страницы будет число 314.
Найдем количество выпавших страниц:
314 – 143 +1 = 172.
Ответ: 172 страницы выпало из книги
№4
Ответ: 
памяти удалено вирусом.
Всю память компьютера примем за единицу.
| Время | Количество памяти, оставшееся в компьютере | Количество памяти, съеденное вирусом |
| 1секунда | 1- |
|
| 2секунда |
|
|
| 3 секунда |
|
|
| 4 секунда |
|
|
| (1+2+3+4) секунды |
|
|
=
Ответ: памяти удалено вирусом.
№5
Ответ:
|
|
На плоскости девять точек, соединенных девятью отрезками через одну. Соединяем точки с нечетными номерами с 1 по 9 , затем 9-ую точку соединяем со 2, далее соединяем точки с четными номерами , 8-ую соединяем с 1. Получили 9 отрезков. Каждый отрезок имеет общие точки ровно с четырьмя другими. Фигура напоминает многоугольник |
№6
Ответ: 54 раза получились четные числа.
| Данное число 1 | Количество четных и нечетных чисел | ||||||||||||||||
| Первый шаг |
| ||||||||||||||||
| +2=3 | +3=4 | ∙2=2 | ∙3=3 | 2ч. и 2неч. | |||||||||||||
| Второй шаг |
| ||||||||||||||||
| +2 | +3 | ∙2 | ∙3 | +2 | +3 | ∙2 | ∙3 | +2 | +3 | ∙2 | ∙3 | +2 | +3 | ∙2 | ∙3 |
| |
| =5 | =6 | =6 | =9 | =6 | =7 | =8 | =12 | =4 | =5 | =4 | =6 |
|
|
|
|
| |
| 2чет. и 2 нечет. | 3чет. и 1 нечет. | 2чет. и 2 нечет | По аналогии 3чет. и 1 нечет | 10ч. и 6неч | |||||||||||||
| Вывод: из нечетного получается 2 четных и 2 нечетных, из четного получается 3 четных и 1 нечетное
| |||||||||||||||||
| Третий шаг Каждое число дает 4 новых числа, поэтому отметим только количество четных и нечетных чисел |
| ||||||||||||||||
| +2,+3, ∙2, ∙3 | +2,+3, ∙2, ∙3 | +2,+3, ∙2, ∙3 | +2,+3, ∙2, ∙3 |
|
|
|
|
|
|
|
|
|
|
|
|
| |
| 2(3ч+1неч) +2(2ч+2неч)= 10ч+6неч | 3(3ч+1неч)+1(2ч+2неч)= 11чет+5неч | 10ч+6неч | 11чет+5неч | 42чет.+22неч. | |||||||||||||
| Найдем количество всех появившихся четных чисел: 2чет. + 10чет + 42чет. = 54 чет. Итого: 54 четных числа | |||||||||||||||||
Ответ: 54 раза получились четные числа.
№7
Ответ: 6 треугольников.
Пусть а, в и с – стороны треугольника, где а – большая сторона и а . Тогда получим треугольники со сторонами:
2010, 2009, 2008;
2010, 2009, 2;
2010, 2009, 3;
2009, 2008, 2;
2009, 2008, 3;
2010, 2008, 3.
Всего треугольников 6.
Ответ: 6 треугольников.
№8
Ответ: 3 минуты.
х мин. – время движения старшего брата,
(х+1) мин. – время движения младшего брата.
1-расстояние до школы,
- скорость старшего брата,
- скорость младшего брата,
х мин –время движения старшего брата до встречи
(х+1) мин. время движения старшего брата до встречи.
Так как до встречи они прошли одно и тоже расстояние, составим уравнение:
х = (х+1),
16х = 12(х+1),
16х = 12х + 12,
4х =12,
х =12:4
х = 3
3минуты старший брат догоняет младшего, вышедшего на 1 минуту раньше.
Ответ: потребуется 3 минуты старшему брату, чтобы догнать младшего брата.
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
