Математическое моделирование в школьном курсе математики

Муниципальное бюджетное образовательное учреждение

«Средняя общеобразовательная школа №75»

Математическое моделирование

Малкова Е. М.

учитель высшей категории

город Ульяновск

Теоретические основы моделирования

"От живого созерцания к абстрактному мышлению
и от него к практике — таков диалектический путь
познания истины, познания объективной реальности".
В.И.Ленин

Люди издавна интересуются, как устроена наша Вселенная. Этот интерес не только чисто познавательный, но и сугубо практический, ибо люди хотели научиться предсказывать периодические явления, связанные с устройством Вселенной, такие, как затмения Солнца и Луны, наступление времен года и т. д.

Для решения этих задач ученые строили свои представления о Вселенной в виде схемы — картины мира, в которой объекты Вселенной — Солнце и звезды, планеты, Земля и Луна изображались точками, движущимися по каким-то кривым — траекториям их движения. Таковы, например, схемы, построенные Птолемеем, в которых центральное место занимала наша Земля, или схема Коперника, в которой центр занимало Солнце. С помощью этих схем ученые решали задачи предсказания отдельных астрономических явлений.

Эти схемы, эти картины мира суть модели Вселенной, а метод исследования Вселенной, нахождения законов о Вселенной и решения задач, связанных с нею, с помощью этих моделей является методом моделирования.

Разрезая конус плоскостями, получаем в сечении различные кривые: окружности, эллипсы, параболы, гиперболы. Математики еще в древности начали изучение этих кривых, результаты которых имеют большое значение для физики, астрономии, техники, военного дела, где очень часто встречаются эти кривые. Однако лишь тогда, когда, пользуясь методом Декарта и Ферма, были составлены уравнения этих кривых, их изучение сразу резко подвинулось вперед и с помощью этих уравнений — моделей кривых конических сечений — были решены все основные задачи, с ними связанные. Заметим, что уравнения выступают в качестве моделей окружности, эллипса, параболы и гиперболы, а эти кривые в свою очередь можно рассматривать как геометрические модели указанных уравнений.

Понятие математического моделирования

Моделирование — это метод исследования каких-либо явлений, процессов или систем объектов, который предполагает создание искусственных или естественных систем (моделей), имитирующих существенные свойства оригинала; использование моделей для определения или уточнения характеристик и рационализации способов построения вновь конструируемых объектов.

Моделирование — одна из основных категорий теории познание: на идее моделирования по существу базируется любой метод научного исследования — как теоретический (при котором используются различного рода знаковые, абстрактные модели), так и экспериментальный (использующий предметные модели).

Математическая модель

Математическая модель, основанная на некотором упрощении, никогда не бывает тождественна рассматриваемому объекту, не передаёт всех его свойств и особенностей, а является его приближённым отображением. Однако благодаря замене реального объекта соответствующей ему моделью появляется возможность математически сформулировать задачу его изучения и воспользоваться для анализа его свойств математическим аппаратом, который не зависит от конкретной природы данного объекта. Этот аппарат позволяет единообразно описать широкий круг фактов и наблюдений, провести их детальный количественный анализ, предсказать, как поведёт себя объект в различных условиях, т.е. прогнозировать результаты будущих наблюдений. Из определения моделей важны две характеристики: модель замещает объект изучения; находится с ним в определённых отношениях. Степень соответствия модели оригиналу может быть различной: подобие, аналогия, изоморфизм (взаимнооднозначное соответствие структур модели и прототипа), гомоморфизм (обобщённое соответствие). Моделирование — это процесс создания моделей и работа с ними. Главные функции моделей — описательная, конструктивная и эвристическая. Описательная функция модели состоит в том, что в исследуемом объекте выделяются и обобщаются существенные компоненты и взаимосвязи между ними. Конструктивная функция модели состоит в её способности служить ориентиром, применять добытые знания в новых ситуациях. Эвристическая функция модели способствует прогнозированию. В зависимости от основной дидактической функции различают три вида моделей: описательные, конструктивные и эвристические. Описательные модели дают возможность сжато излагать информацию и воспроизводить её. Конструктивные модели больше ориентированы на применение знаний, эвристические — на овладение новыми знаниями, обобщение и систематизацию. При этом форма моделей может быть различной: модельная схема, знаковая модель, графическая, образная и т.д.

Математическое моделирование как метод познания

Метод построения математических моделей — метод математического познания действительности изучаемых реальных объектов или объектов, уже описанных в других областях знаний, с целью их более глубокого изучения и решения всех, возникающих в этих реальных ситуациях задач с помощью математического аппарата. Математическая модель — это приближённое описание какого-нибудь класса явлений, выраженное на языке какой-нибудь математической теории (с помощью системы алгебраических уравнений и неравенств, дифференциальных или интегральных уравнений, функций, системы геометрических предложений, векторов и т.п.). Математическое моделирование — описание анализируемого объекта внешнего мира с помощью математической символики. Как алгоритм математической деятельности метод математического моделирования содержит три этапа: Формализация: построение математической модели объекта (явления, процесса); Исследование полученной модели, т. е. решение полученной математической задачи средствами математики; Интерпретация полученного решения с точки зрения исходной ситуации. При этом должны соблюдаться следующие требования: Модель должна адекватно отражать наиболее существенные (с точки зрения определенной постановки задачи) свойства объекта, отвлекаясь от несущественных его свойств; Модель должна иметь определенную область применимости, обусловленную принятыми при её построении допущениями; Модель должна позволять получать новые знания об изучаемом объекте. Во введении понятий математическая модель и моделирование позволяют решать в учебном процессе следующие актуальные задачи: развитие мышления и интеллекта; формирование мировоззрения; овладение элементами математической культуры. После того как математическая модель построена, возможны два случая: Полученная конкретная модель принадлежит к уже изученному в математике классу моделей и тогда математическая задача решается уже известными методами; Эта модель не укладывается ни в одну из известных схем (классов) моделей, разработанных в математике, и тогда возникает внутриматематическая проблема исследования нового класса моделей, что приводит к дальнейшему развитию одной из существующих математических теорий или к появлению новой. Это развитие математических теорий находит затем применение к изучению той области знаний, в которой возникла исходная задача, а также и других объектов реального мира, приводящих к математическим объектам того же класса. Обучение, как правило, должно начинаться с рассмотрения реальных ситуаций и возникающих в них задач ("подводящих" задач) с поиска средств для их математического описания, построения соответствующих математических моделей. Затем объектом изучения становятся уже сами эти модели, их исследование, приводящее к расширению теоретических знаний учащихся. После того, как соответствующая теория построена, её аппарат применяется к решению исходной задачи, а также других задач из других областей, но приводящих к моделям этого же класса. Так можно строить изучение каждого нового вида функций, уравнений, производной, интеграла, операций над векторами, вывода формул вычисления площадей и объемов и т.п.

Классификация моделей

В школьной практике важно различать материальные и идеальные (мысленные) модели. Идеальные модели, применяемые при изучении естественно-математических дисциплин, позволяют решать задачи, требующие переноса знаний в новую ситуацию. Ведь модель — это мостик от абстрактного к конкретному, по которому движется мысль школьника. В зависимости от основной дидактической функции различают три вида моделей: описательные, конструктивные и эвристические. Описательные модели дают возможность сжато излагать информацию и воспроизводить её. Конструктивные модели больше ориентированы на применение знаний, эвристические — на овладение новыми знаниями, обобщение и систематизацию. При этом форма моделей может быть различной: модельная схема, знаковая модель, графическая, образная и т.д. Мордкович пишет: "Нам нужно научиться описывать реальные ситуации словами (словесная модель), алгебраически (алгебраическая модель), графически (графическая модель). Бывают еще геометрические модели реальных ситуаций — они изучаются в курсе геометрии. Графические модели также иногда называют геометрическими, а вместо термина "алгебраическая модель" используют термин "аналитическая модель". Все это — виды математических моделей." Костевич, Лапко: "Математические модели, используемые в исследовании явлений, можно разделить на статистические и аналитические. Статистические модели позволяют наиболее полно учитывать все связи, факторы, описывающие явление, и заменять однократное исследование сложной модели многократным исследованием простых моделей. Аналитические модели с помощью алгебраических, дифференциальных, интегральных уравнений позволяют установить формульные зависимости между основными факторами явлений. Чаще всего применяются совместно аналитические и статистические модели явлений." Штофф В.А. : "Выделяют вещественные и мысленные типы моделей. Вещественные модели допускают предметное преобразование. Первый тип подразделяется на два подтипа: модели, отображающие пространственные особенности объектов (например, макеты); модели, имеющие физическое подобие оригинала (например, модель плотины). Математические модели относятся к мысленным. Среди них можно выделить: образно-графические (схемы, диаграммы, чертежи, рисунки и т. п.); знаковые модели (пример, формула алгебраического уравнения и т.п.); смешанные (например, таблицы). Знаковые модели требуют специальной интерпретации, без которой — сами по себе — они теряют функцию моделей." Можно классифицировать модели по отраслям наук: математические модели в физике, биологии, социологии и т.д. Есть классификация по применяемому математическому аппарату: модели, основанные на применении обыкновенных дифференциальных уравнений, дифференциальных уравнений в частных производных, стохастических методов, дискретных алгебраических преобразований и т.д. Человек, интересующийся общими закономерностями моделирования в разных науках безотносительно к математическому аппарату, ставящий на первое место цели моделирования, скорее заинтересуется такой классификацией: дескриптивные (описательные модели), оптимизационные модели, многокритериальные модели, игровые модели, имитационные модели.

Примеры использования математического моделирования в школьном курсе математики

Широко известны серьезные трудности, которые испытывают учащиеся при решении задач.

Первая трудность состоит в математизации предложенного текста, т.е. в составлении математической модели, которая может представлять собой уравнение, неравенство или их систему, диаграмму, график, таблицу, функцию и т.д.

Для того, чтобы перевести содержание задачи на математический язык, учащемуся необходимо тщательно изучить и правильно истолковать его, формализовать вопрос задачи, выразив искомые величины через известные величины и введенные переменные.

Вторая трудность — составление уравнений и неравенств, связывающих данные величины и переменные, которые вводит учащийся.

Третья трудность — это решение полученной системы уравнений или неравенств желательно наиболее рациональным способом.

Способ, разработанный Левитас Г.Г.

Левитас Г.Г. использует следующий способ обучения школьников алгебраическому методу решения текстовых задач.

Текстовой задачей, по его словам, назовем не математическую по фабуле задачу, решаемую математически. Например, задача "У Кати и Поли вместе 12 кукол; у Кати на две куклы меньше. Сколько кукол у каждой из них?" — не математическая по фабуле. Но её можно решить математическим методом, моделируя ситуацию уравнением х+(х+2)=12.

Для решения текстовой задачи мы переводим её на математический язык, т.е. создаём её математическую модель. Овладение навыками математического моделирования, по мнению Левитас, — едва ли не самое важное, чему мы учим детей на уроках математики. Одна из причин неуспеха,как пишет Левитас Г.Г., состоит в неправильном порядке обучения методу алгебраического решения текстовых задач, а именно в неправильном порядке их перевода на язык математики.

Ведь как вообще совершается перевод с одного языка на другой? Иногда он идёт синхронно. Вы читаете лёгкий для перевода текст и тут же излагаете его на другом языке. Именно так переводит учитель математики лёгкие для него текстовые задачи из школьного курса. Он сразу видит что именно выгодно принять за х, что нужно выразить через х, каким будет уравнение. И учит детей работать именно в таком порядке. И действительно, лёгкие для школьника задачи он решает именно так.

Но вот встретилась задача потруднее. Что обозначать через х? Какие именно неизвестные величины выражать через х? Как составлять уравнение?

Рассмотрим, например, такую задачу. " Когда первый из двух шашечных турниров завершился, во втором было сыграно столько же партий, сколько в первом, и осталось сыграть ещё три тура. Известно, что оба турнира игрались в один круг и что число участников во втором туре было чётным. Сколько партий игралось в каждом туре второго турнира?"

Левитас предлагает сначала составить схему уравнения:

число партий + число партий в = число партий во

в первом турнире трёх турах второго втором туре.

турнира

Затем надо выбрать основные неизвестные так, чтобы через них можно было выразить каждую из величин, имеющихся в этой схеме. Если обозначить через х число участников первого турнира, а через у число участников второго турнира, то получим уравнение:

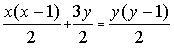
Описанная последовательность действий и есть тот способ, которым Левитас учит детей решать не получающиеся у них задачи: составь схему уравнения, выбери обозначения, составь уравнение …

Например, если школьнику трудно решить приведённую выше задачу с куклами, он добивается от него составления такой схемы уравнения:

(число кукол у Кати)+(число кукол у Поли)=12,

и только после этого он занимается поисками, связанными с переводом на математический язык выражений, стоящих в скобках. Понятно, что та же задача допускает и иное истолкование:

(число кукол у Поли)-(число кукол у Кати)=2,

что приводит к иным обозначениям.

Особенность этого способа заключается в том, что моделирование — перевод на математический язык — проводится в два приёма. Сначала русский текст задачи частично сохраняется и выступает совместно с элементами математического языка: знаками действий и знаком равенства. И только после этого естественный язык полностью заменяется математическим. Именно так, постепенно, переводим мы трудную для нас фразу с одного языка на другой.

Переформулирование задачи

Сергей Леонидович Рубинштейн характеризовал решение задач человеком как процесс их переформулирования.

Рассмотрим пример переформулирования задач в процессе анализа и решения.

Задача 1

Некоторая коллекция значков была размещена в коробках, каждая из которых имела 10 отделении. В некоторые отделения коробок были положены значки, по одному в отделение, другие отделения были еще пустые. Любые две коробки этой коллекции отличались друг от друга хотя бы наличием или отсутствием значков в одном и том же отделении. Очевидно, что наибольшее число значков в коробке равно 10, а наименьшее — нуль (коробка пустая). Сколько коробок в этой коллекции?

Эта задача, конечно, носит несколько необычный характер. Но вот подобная ей задача, имеющая уже более реальный характер, полученная из задачи 1 с помощью такого переформулирования: каждому отделению коробки поставим в соответствие электрическую лампочку, тогда наличию или отсутствию в нем значка соответствует одно из возможных состояний лампочки (горит или не горит). В результате получаем такую задачу.

Задача 2

В квартире 10 лампочек. Сколько существует различных способов освещения квартиры? Два способа освещения считаются различными, если они отличаются состоянием хотя бы одной лампочки. Каждая лампочка может гореть и не гореть. Случай, когда все лампочки не горят,— это тоже способ освещения.

Хотя эта задача более реальная и явление, в ней описанное, более наглядное, но и ее решение не очевидно. Чтобы легче подсчитать все различные способы освещения квартиры (или число коробок), изобразим каждую лампочку (каждое отделение) в виде квадрата, а ее состояние будем отмечать знаком "+", если лампочка горит (значок имеется), и знаком "-" в противном случае. Тогда каждому способу освещения квартиры (каждой коробке) будет соответствовать строка из десяти квадратиков со знаком "+" или "-". Число же таких строк в таблице и есть искомое число различных способов освещения квартиры (число коробок). Получаем такую задачу.

Задача 3

Имеется прямоугольная таблица, содержащая 10 столбцов. В каждой клеточке этой таблицы поставлен знак "+" или "-". Любые две строки таблицы отличаются знаком в клеточках, стоящих хотя бы в одном и том же столбце. Какое наибольшее число строк имеет эта таблица?

Если решение и этой задачи вам не очевидно, то можно построить еще более прозрачную задачу следующим образом. Будем рассматривать каждую строку таблицы, о которой идет речь в предыдущей задаче, как десятизначное число, составленное из цифр 1 и 0 (цифра 1 соответствует знаку "+" в клеточке, а цифра 0 — знаку "-"). Тогда задача 3 переформулируется в такую.

Задача 4

Сколько различных десятизначных чисел можно образовать из цифр 0 и 1? При этом числа, в записи которых стоят слева одни нули (например, 0100001101, или 000000001, или даже 00000000001), также рассматриваются.

Решение этой последней задачи уже очевидно. На каждом месте в записи десятизначного числа могут стоять лишь цифры 1 или 0. Поэтому имеется всего лишь две комбинации цифр на каждом месте. Эти комбинации независимы друг от друга, ибо проставление цифры на данном месте в записи числа не зависит от того, какие цифры стоят на других местах. Поэтому общее число комбинаций или возможных десятизначных различных чисел равно 2¹⁰ =1024.

Итак, общее число коробок из задачи 1, число способов освещения квартиры из задачи 2, число строк в таблице из задачи 3 и число десятизначных чисел из задачи 4 равно 1024.

Задачи 2-4 были получены из задачи 1 с помощью ее переформулирования. Чем же они являются для нее? Оказывается, что все они являются ее моделями, следовательно, переформулирование задачи 1 явилось способом ее моделирования, построения ее моделей.

Покажем еще на одном примере применение моделирования при решении задач.

3адача 5 (задача Ньютона)

Трава на лугу растет одинаково густо и быстро. Известно, что 70 коров поели бы ее за 24 дня, а 30 коров — за 60 дней. Сколько коров поели бы всю траву за 96 дней?

Решение. Эта задача практическая, текстовая. Для того чтобы ее решить, надо составить уравнение или систему уравнений, которые представляют собой модель данной задачи.

Заданные в задаче величины — количество коров и числом дней — не связаны непосредственно, поэтому введем следующие вспомогательные неизвестные — параметры для установления связи между основными величинами. Пусть на лугу первоначально было "а" единиц травы, и ежедневно на нем, вырастает "b" единиц травы. Пусть каждая корова за 1 день съедает "c" единиц травы. Тогда в соответствии с условием получаем.

За 24 дня всего вырастет (а+24b) единиц травы, которую за это время съедают 70 коров. Они съедают 24*70с=1680с, следовательно

a+24b=1680с. (1)

По условию, что 30 коров съедают всю траву за 60 дней, получаем:

а+60b=1800с. (2)

За 96 дней на лугу вырастет всего а+96b единиц травы, которую съедят искомое х число коров, они съедят всего 96х*с единиц травы, следовательно, получим такое уравнение:

a+96b=96х*с. (3)

Уравнения (1), (2) и (3) образуют систему, которая и есть модель исходной задачи. Эту систему нам нужно решить относительно искомого х. Вычтем почленно из уравнения (2) уравнение (1), получим:

36b=120с.

Отсюда

с=0,3b. (4)

Подставим полученное значение с в уравнение (1):

а+24b=504b,

отсюда

а=480b. (5)

Подставим выражения "с" и "а" из (4) и (5) в (3), получим:

480b+96b=28,8х*b

или 576b=28,8х*b,

отсюда, сократив предварительно на "b", найдем: х=20. Ответ: 20 коров.

Список литературы

1. Баврин И.И. Начала анализа и математические модели в естествознании и экономике. М.:Просвещение.1999.

2. Епишева О.Б. Общая методика преподавания математики в средней школе: Курс лекций. Тобольск: Изд. ТГПИ им. Д.И.Менделеева.1997.

3. Паламарчук В.Ф. Школа учит мыслить. М.:Просвещение. 1987

4. Фридман Л.М., Турецкий Е.Н. Как научиться решать задачи. М.:Просвещение.1984.

5. Хеннер Е.К., Шестаков А.П. Математическое моделирование. Пособие для учителя. Пермь.1995.

6. Штофф В.А. Моделирование и философия. М.,Л.1966.

7. Левитас Г.Г. Об алгебраическом решении текстовых задач.//Математика в школе, №8, с.13.2000.

8. Мордкович А.Г. Алгебра. Учебник для 7 класса общеобразовательной школы. М.:Мнемозина.1997.

9. Чаплыгин В.Ф. Некоторые методические соображения по решению текстовых задач.//Математика в школе, №4, с.28.2000.

10. Большая энциклопедия Кирилла и Мефодия 2000."Кирилл и Мефодий".1999.