Основні положення
Статистика – це наука, що збирає, обробляє та вивчає різні дані, пов’язані з масовими явищами, процесами, подіями. Предметом вивчення статистики є кількісна сторона масових явищ (від випуску продукції до катастроф у природі та політичних баталій) у зв’язку з їхньою якісною стороною. Розділ прикладної математики, який досліджує кількісні характеристики називається математичною статистикою. Вона присвячена математичним методам систематизації, обробки та використання статистичних даних для наукових та практичних висновків.
Статистичне спостереження – перший етап статистичного дослідження. Воно буває суцільним та несуцільним. Видами несуцільного спостереження є: вибіркове, спостереження основного масиву та анкетування.
Найпоширенішим видом є вибіркове спостереження. Обстеженню підлягають відібрані певним чином одиниці усієї сукупності, а результати обчислення цієї частини сукупності поширюються на всю сукупність в цілому.
Багато графіків мають схожу форму, незважаючи на те, що досліджувались зовсім інші ознаки. Це пояснюється тим, що врожайність, маса, зріст, розмір взуття – випадкові величини. А найбільш поширеним є нормальний (гаусів) розподіл частот.
Вибірки характеризують центральними тенденціями: середнім значенням, модою і медіаною. Статистика оперує такими середніми значеннями: середнє арифметичне (вибіркове середнє), середнє квадратичне, середнє кубічне, середнє геометричне, середнє гармонічне та ін. Всі перераховані типи середніх можуть бути розраховані для випадків, коли кожна з ознак ряду зустрічається тільки один раз (тоді середня називається простою) та коли ці ознаки повторюються. Для характеристики ряду один з перерахованих типів середніх вибирається не довільно, а в залежності від особливостей явища, для якого вираховується середнє. Практично під час вибору того чи іншого типу середнього слід виходити з принципу осмислення результату. Лише тоді середня використана вільно, коли в результаті виходять величини, які мають реальний зміст. Варто пам’ятати, що середня тільки в тому випадку є узагальнюючою характеристикою, якщо вона застосовується до однорідної сукупності.
Математична статистика
Основною задачею математичної статистики є розробка методів одержання науково обгрунтованих висновків про поведінку масових явищ і процесів за результатами спостережень.Умовно дану задачу можна розчленити на дві. Першою з них є розробка методів збору і групування статистичних даних, одержаних в результаті спостережень, опрацювання статистичних звітів чи даних у результаті спеціально поставлених експериментів.
Друга задача полягає в розробці методів аналізу статистичних даних залежно від мети. Сюди належать:
Висновки за допомогою методів математичної статистики, зроблені за зібраними статистичними даними, повинні правильно відображати загальні ймовірнісні характеристики процесу, що досліджується.
Сучасна математична статистика розробляє способи визначення числа необхідних випробувань до початку дослідження(планування експерименту) , а в ході дослідження вказує, як проводити послідовний аналіз даних. Тому математичну статистику визначають як науку про прийняття рішень в умовах невизначеності. Статистичне спостереження – перший етап статистичного дослідження. Спостереження за ступенем повноти охоплення безпосередньо пов”язане з математикою. Воно поділяється на суцільне – у якому реєструється ознака всіх без винятку одиниць, що входять у сукупність(перепис населення), та несуцільне – під час якого реєструють ознаки лише частини одиниць досліджуваної сукупності, і за частиною роблять висновок про всю сукупність.Видами несуцільного спостереженняє: вибіркове спостереження, спостереження основного масиву і анкетне спостереження.
Основними поняттями в математичній статистиці є генеральна та вибіркова сукупності.Під генеральною сукупністю розуміємо множину об”єктів В, що підлягає статистичному дослідженню. Підмножину А множини В відібраних об”єктів називають вибірковою сукупністю, або вибіркою. Об”єкти множини можуть характеризуватися однією або кількома ознаками, які можуть бути якісними і кількісними. Якісна ознака характеризує певну властивість або стан, якими володіють об”єкти генеральної сукупності(наприклад, професія, якість продукції тощо). Кількісна ознака вимірюється числом.
Часто використовують геометричне зображення вибірки, за допомогою якого можна зробити певні теоретичні висновки. Наочно зобразити ці дані можна за допомогою емпіричної функції розподілу, полігонів частот та відносних частот або стовпчастої діаграми, яку у математичній статистиці називають гістограмою. Їй надають перевагу, коли зображують не більше одного розподілу. Але якщо треба порівняти два або більше розподілів, то для цього краще підходять полігони частот, бо їх можна накласти один на одного при меншому перетині ліній.
В результаті статистичної обробки матеріалів можна порахувати число одиниць, що мають конкретні ознаки. Зміну цієї ознаки називають варіацією, а кожне окреме значення ознаки – варіантою. Абсолютне число, що показує скільки разів зустрічається та чи інша варіанта, - частотою. Якщо здійснити групування варіант за окремими значеннями ознаки, матимемо дискретне(перервне) групування.
Вибірки характеризують центральними тенденціями: середнім значенням, модою і медіаною. Статистика оперує такими середніми значеннями: середнє арифметичне(вибіркове середнє), середнє квадратичне, середнє кубічне, середнє геометричне, середнє гармонічне та ін. Всі перераховані типи середніх можуть бути розраховані для випадків, коли кожна з варіант варіаційного ряду зустрічається тільки один раз( тоді середня називається простою) та коли варіанти повторюються. Для характеристики варіаційного ряду один з перерахованих типів середніх вибирається не довільно, а в залежності від особливостей явища, для якого вираховується середнє. Практично під час вибору того чи іншого типу середнього слід виходити з принципу осмислення результату. Лише тоді середня використана вірно, коли в результаті виходять величини, які мають реальний зміст. Варто пам”ятати, що середня тільки в тому випадку є узагальнюючою характеристикою, якщо вона застосовується до однорідної сукупності. Науковою основою статистичного аналізу є метод статистичного групування, тобто розчленування сукупності на якісно однорідні групи.
Середнє квадратичне відхилення:
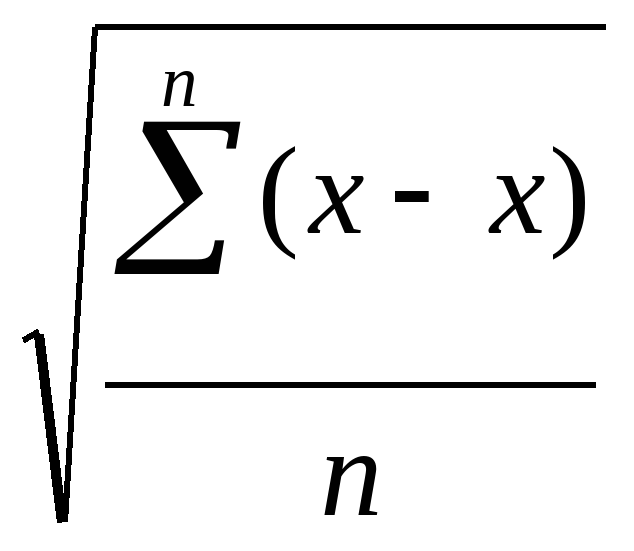 =
= 
В якості характеристики варіаційного ряду використовують моду – варіанту, яка трапляється найчастіше. Для дискретного ряду мода, що є характеристикою варіаційного ряду, визначається за частотами варіант. Варіаційні ряди, у яких частоти варіант, рівновіддалених від середньої, рівні між собою, називаються симетричними. Особливість симетричних варіаційних рядів полягає у рівності трьох характеристик – середньої арифметичної, моди та медіани.Мода використовується у практиці торговельної статистики під визначення купівельного попиту на товари, рівня цін на ринках тощо. Медіаною називають значення середнього елемента варіаційного ряду. Якщо обсяг вибірки n=2m + 1непарний, то медіаною буде значення елемента варіаційного ряду з номером m + 1. Якщо обсяг вибірки n=2m парний, то медіаною буде середнє значення елементів варіаційного ряду з номерами m і m + 1.Медіана має таку властивість: сума абсолютних величин відхилень елементів вибірки від медіани менша, ніж від будь-якої іншої величини.
Завдання математичної статистики – дійти певних висновків щодо експериментальних даних. При цьому мається на увазі, що до експериментів застосовуються теоретико-ймовірнісні концепції. Точніше, задачі математичної статистики можна сформулюавти з різним ступенем загальності з різноманітних точок зору. Теорія статистичного виведення – це формалізована система методів розв”язування задач, що характеризуються намаганням вивести властивості великого масиву даних обстеженням вибірки.
Задачі з математичної статистики
Задача 1. 10 абітурієнтів дістали на трьох екзаменах таку кількість балів: 10;9;11;10;12;14;13;15;9;10.Побудувати статистичний розподіл цих даних, заповнивши таблицю:
| Кількість балів | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| Кількість абітурієнтів |
|
|
|
|
|
|
|
Задача 2. За таблицею побудуйте гістограму розподілу учнів класу за роками народження:
| Рік народження | 1991 | 1992 | 1993 | 1994 |
| Кількість учнів | 1 | 20 | 3 | 2 |
Задача 3.Рівень рентабельності підприємства легкої промисловості характеризується даними:
| Рівень рентабельності | До 5 | 5-10 | 10-15 | 15-20 | 20-25 | 25-30 |
| Кількість підприємств | 3 | 8 | 16 | 22 | 24 | 18 |
Побудувати полігон розподілу частот та гістограму.
Задача 4.За даними таблиці про врожайність пшениці на різних ділянках посівної площі побудувати гістограму
| Врожайність ц/га | 20-25 | 25-30 | 30-35 | 35-40 | 40-45 | 45-50 |
| Частка ділянки від загальної посівної площі % |
5 |
10 |
33 |
21 |
25 |
6 |
Задача 5.Програма кредитування населення у 2004 році банком”Мрія” складала:
| місяць | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Планове кредитування(тис.грн.) | 12 | 10 | 12 | 9 | 8 | 11 | 10 | 9 | 10 | 12 | 12 | 15 |
| Дійсне кредитування(тис.грн.) | 14 | 9 | 11 | 6 | 8 | 12 | 9 | 7 | 9 | 17 | 21 | 23 |
Побудувати полігон частот.Чи доцільно у даній задачі використовувати гістограму?
Задача 6.Рівні води в річці Прип”ять по відношенню до номіналу вимірювали протягом 50 весняних паводків і дані вносили в таблицю:
| Рівень,см | 0-25 | 25-50 | 50-75 | 75-100 | 100-125 | 125-150 | 150-175 | 175-200 | 200-225 | 225-250 | 250-275 | 275-300 |
|
| Кількість випадків | 0 | 1 | 4 | 6 | 7 | 8 | 5 | 4 | 6 | 4 | 3 | 2 |
|
Побудувати за цими даними гістограму та полігон частот.
Задача 7. Знайти центральні тенденції вибірки: 1,5; 1,4; 1,8; 1,5; 0; 2,1; 1,5; 2,1; 1,8.(моду, середнє значення і медіану).
Задача 8. За розв”язання задач учасники незалежного тестування отримали: від 0 до 5 балів – шість учнів; від 6 до 10 балів – десять учнів; від 11 до 15 балів – чотирнадцять учнів; від 16 до 20 – чотири; від 21 до 25 – шість; від 26 до 30 – два учні.Скласти частотну таблицю, побудувати гістограму та визначити центральні тенденції вибірки.
Задача 9.Місцевому молокозаводу потрібно спланувати випуск кисломолочної продукції на місяць.Як це зробити?
Задача 10. На одному з відрізків залізниці планується створити зупинку пасажирського поїзда. Розподіл населених пунктів з чисельністю їх населення наведено в таблиці.
| На якому кілометрі залізниці розташований населений пункт,км |
10 |
12 |
15 |
25 |
28 |
30 |
33 |
| Чисельність населення, тис.чол. |
5 |
2 |
3 |
10 |
1 |
4 |
6 |
На якому кілометрі залізниці потрібно розташувати цю зупинку, щоб сумарна відстань, яку покриватимуть потенційні пасажири до цієї зупинки, була найменшою.
Задача 11.На автостраді довжиною 100 км є 10 автостоянок. Для проектування будівництва заправки були зібрані дані про число допустимих поїздок до неї з кожної автостоянки. Результати занесені в таблицю
| На якому кілометрі розміщена стоянка |
7 |
26 |
28 |
37 |
40 |
46 |
60 |
78 |
86 |
92 |
Всьго поїздок |
| Проектоване число поїздок |
10 |
15 |
5 |
20 |
5 |
25 |
15 |
30 |
10 |
65 |
200 |
Потрібно спроектувати заправку так, щоб загальний пробіг машин до неї був найменшим.
Задача 12.Обчислити середній стаж вчителів нашого міста, використовуючи дані таблиці
| Стаж,років | До 4 | 4-8 | 8-12 | 12-16 | Більше16 | всього |
| Кількість вчителів,у% |
12,0 | 18,5 |
30,4 |
26,0 |
13,1 |
100 |
Задача 13.Розподіл сімей по кількості дітей характеризується наступними даними
| Кількість дітей | 0 | 1 | 2 | 3 | 4 | всього |
| Кількість сімей,% | 10 | 30 | 40 | 15 | 5 | 100 |
Визначити середню кількість дітей у сім”ї.
Тема: Статистика та її методи. Наочне представлення статистичного розподілу: полігон та гістограма. Мода і медіана. Поняття середнього у статистиці. Завдання математичної статистики.
Мета:
Ознайомити учнів з поняттями статистика та математична статистика.
Навчити будувати та проводити аналіз гістограм.
Розкрити суть моди та медіани.
Ввести поняття середнього у статистиці.
Узагальнити завдання математичної статистики.
Математика оперує ідеальними об’єктами - числами, а за допомогою чисел передають кількісні та якісні характеристики предметів. Одна справа, коли чисел 10 чи 20, і зовсім інша – коли десятки тисяч.
Статистика – це наука, що збирає, обробляє та вивчає різні дані, пов’язані з масовими явищами, процесами, подіями. Предметом вивчення статистики є кількісна сторона масових явищ (від випуску продукції до катастроф у природі та політичних баталій) у зв’язку з їхньою якісною стороною. Розділ прикладної математики, який досліджує кількісні характеристики називається математичною статистикою. Вона присвячена математичним методам систематизації, обробки та використання статистичних даних для наукових та практичних висновків.
Статистичне спостереження – перший етап статистичного дослідження. Воно буває суцільним та несуцільним. Видами несу цільного спостереження є: вибіркове, спостереження основного масиву та анкетування.
Анкета для учнів: чи комфортно вам на сьогоднішньому уроці?
Найпоширенішим видом є вибіркове спостереження. Обстеженню підлягають відібрані певним чином одиниці усієї сукупності, а результати обчислення цієї частини сукупності поширюються на всю сукупність в цілому.
Систематизувати зібрані дані найкраще у таблицю. Зазвичай ці таблиці складаються з двох рядків: перший – статистичний підмет, це та сукупність про яку йдеться мова, другий – статистичний присудок, це ті ознаки, які характеризують статистичний підмет.
Задача 1. Взуттєвикам треба знати, скільки взуття слід випускати того чи іншого розміру. Опитати всіх, тобто десятки мільйонів чоловіків і жінок, надто дорого і довго. Тому роблять вибірку: наприклад, опитали 60 жінок, їх розміри взуття записали в таблицю.
| 23.5 | 24 | 23 | 24.5 | 23 | 22.5 | 24.5 | 22.5 | 23.5 | 23.5 | 23.5 | 23.5 |
| 25.5 | 21 | 24 | 25 | 23.5 | 22 | 23 | 24.5 | 23 | 24.5 | 23 | 24.5 |
| 25 | 24 | 21.5 | 23.5 | 24.5 | 22.5 | 22 | 23.5 | 26.5 | 25.5 | 25 | 26 |
| 24 | 23 | 21 | 25 | 24.5 | 23 | 23.5 | 23.5 | 23 | 22 | 24.5 | 23.5 |
| 21.5 | 24.5 | 21.5 | 22 | 23.5 | 23 | 22 | 24.5 | 25.5 | 24.5 | 25 | 22 |
Для зручності її групують у класи (за розмірами взуття) і відмічають, скільки значень вибірки містить кожен клас. (Учень заповнює на дошці).
| розмір | 21 | 21.5 | 22 | 22.5 | 23 | 23.5 | 24 | 24.5 | 25 | 25.5 | 26 | 26.5 |
| кількість |
|
|
|
|
|
|
|
|
|
|
|
|
Такі таблиці називають частотними.
Інд. завдання: (3 хв.)
Задача 1. 10 абітурієнтів дістали на трьох екзаменах таку кількість балів: 10; 9; 11; 10; 12; 14; 13; 15; 9; 10. Побудувати статистичний розподіл цих даних, заповнивши таблицю:
| Кількість балів | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| Кількість абітурієнтів |
|
|
|
|
|
|
|
За частотною таблицею можна побудувати стовпчасту діаграму (гістограму), яка дає наочне представлення даних таблиці. На практиці прийнято зображувати гістограму у формі контура, а не окремими стовпцями.
Задача 2. За таблицею побудуйте гістограму розподілу учнів класу за роками народження (учень працює біля дошки).
| Рік народження | 1990-1991 | 1991-1992 | 1992-1993 | 1993-1994 |
| Кількість учнів | 1 | 20 | 3 | 2 |
Інд. завдання: (5 хв.)
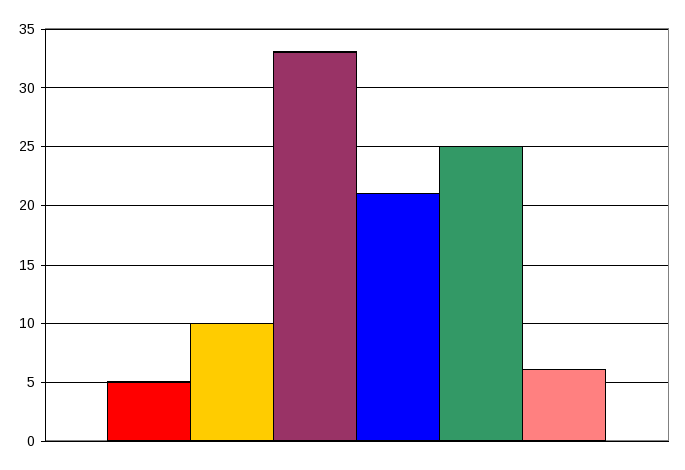
Задача 2. За даними таблиці про врожайність пшениці на різних ділянках посівної площі побудувати гістограму.
| Врожайність ц/г | 20-25 | 25-30 | 30-35 | 35-40 | 40-45 | 45-50 |
| Частка ділянки від загальної посівної площі % |
5 |
10 |
33 |
21 |
25 |
6 |
Задача 3. Рівні води в річці Прип’ять по відношенню до номіналу вимірювали протягом 50 весняних паводків і дані вносили в таблицю:
| Рівень, см | 0-25 | 25-50 | 50-75 | 75-100 | 100-125 | 125-150 | 150-175 | 175-200 | 200-225 | 225- 250 | 250-275 | 275-300 |
| Кількість випадків | 0 | 1 | 4 | 6 | 7 | 8 | 5 | 4 | 6 | 4 | 3 | 2 |
Побудувати за цими даними гістограму та полігон частот.
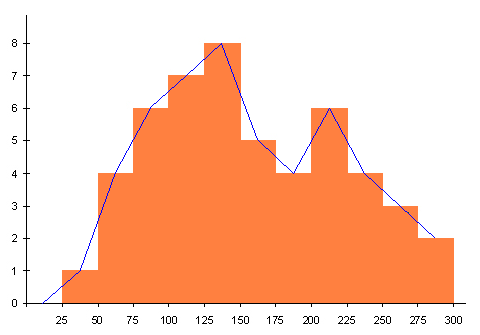
Побудова полігона розподілу нагадує побудову гістограми. В гістограмі кожен стовпчик закінчується горизонтальною лінією, причому на висоті, що відповідає частоті в цьому розряді. А в полігоні він закінчується точкою на середині свого розрядного інтервалу на такій самій висоті.
Завдання для групи (5 хв.).
Задача 3. Програма кредитування населення у 2004 році банком „Мрія” складала:
| місяць | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Планове Кредитування (тис. грн. ) | 12 | 10 | 12 | 9 | 8 | 11 | 10 | 9 | 10 | 12 | 12 | 15 |
| Дійсне Кредитування (тис. грн. ) | 14 | 9 | 11 | 6 | 8 | 12 | 9 | 7 | 9 | 17 | 21 | 23 |
Побудувати полігон частот. Чи доцільно у даній задачі використовувати гістограму?
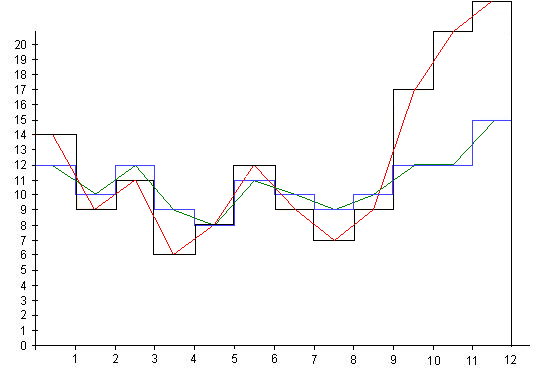
Багато графіків мають схожу форму, незважаючи на те, що досліджувались зовсім інші ознаки. Це пояснюється тим, що врожайність, маса, зріст, розмір взуття – випадкові величини. А найбільш поширеним є нормальний (гаусів) розподіл частот.
Вибірки характеризують центральними тенденціями: середнім значенням, модою і медіаною. Статистика оперує такими середніми значеннями: середнє арифметичне (вибіркове середнє), середнє квадратичне, середнє кубічне, середнє геометричне, середнє гармонічне та ін. Всі перераховані типи середніх можуть бути розраховані для випадків, коли кожна з ознак ряду зустрічається тільки один раз (тоді середня називається простою) та коли ці ознаки повторюються. Для характеристики ряду один з перерахованих типів середніх вибирається не довільно, а в залежності від особливостей явища, для якого вираховується середнє. Практично під час вибору того чи іншого типу середнього слід виходити з принципу осмислення результату. Лише тоді середня використана вільно, коли в результаті виходять величини, які мають реальний зміст. Варто пам’ятати, що середня тільки в тому випадку є узагальнюючою характеристикою, якщо вона застосовується до однорідної сукупності. Найпростішою є характеристика „ в середньому”. Та вона може виявитись досить бідною. Зрозуміти це допоможе цитата з книги Фелікса Кривина „Подражание театру”:
„Не беда, что Янус был двулик,
в общем- то он жизнь достойно прожил.
Пусть он был одним лицом ничтожен,
Но зато другим лицом – велик.
Пусть в одном лице он был пройдоха,
Но в другом был честен и правдив.
Пусть с людьми он был несправедлив,
Но с богами вёл себя неплохо.
Пусть подчас был резок на язык,
Но подчас довольно осторожен.
Не беда, что Янус был двулик.
В среднем он считается хорошим”.
Заслухати завдання групи!
Я прошу самостійно опрацювати та сформулювати означення основних тенденцій вибірки.
Мода – це те значення вибірки, яке трапляється найчастіше.
Медіана – це число, яке „поділяє” навпіл упорядковану сукупність усіх значень вибірки.
Задача 4. Знайти центральні тенденції вибірки: 1,5; 1,4; 1,8; 1,5; 0; 2,1; 1,5; 2,1; 1,8 (моду, середнє значення і медіану).
Мода: 1,5.
Середнє арифметичне: 1,52.
Медіана: 1,5.
Медіана має таку властивість: сума абсолютних величин відхилень елементів вибірки від медіани менша, ніж від будь-якої іншої величини.
Задача 5. На автостраді довжиною 100 км є 10 автостоянок. Для проектування будівництва заправки були зібрані дані про число допустимих поїздок до неї з кожної автостоянки. Результати занесені в таблицю
| На якому кілометрі Розміщена стоянка |
7 |
26 |
28 |
37 |
40 |
46 |
60 |
78 |
86 |
92 | Всього поїздок |
| Проектоване число поїздок |
10 |
15 |
5 |
20 |
5 |
25 |
15 |
30 |
10 |
65 |
200 |
Потрібно спроектувати заправку так, щоб загальний пробіг машин до неї був найменшим.
Варіант 1. Якщо збудувати заправку на середині автостради, тобто на 50-му кілометрі (середнє арифметичне), то пробіг з врахуванням числа поїздок складатиме:
В одному напрямку
43*10+24*15+22*5+13*20+10*5+4*25 = 1310 км
В іншому напрямку
10*15+28*30+36*10+42*65 = 4080 км
Загальний пробіг в обидва напрямки 1310 + 4080 = 5390 км
Варіант 2. Зменшення пробігу можна добитись якщо заправку збудувати на
(7*10+26*15+28*5+37*20+40*5+46*25+60*15+78*30+86*10+92*65) /(10+15+5+20+25+25+15+30+10+65)=63,85, тобто на середній ділянці шосе з врахуванням числа поїздок (середнє арифметичне зважене). У цьому випадку пробіг буде складати по 2475,75 км в обидва напрямки, тобто загальний пробіг 4951,5 км менший, ніж у першому варіанті на 5390-4951,5=438,5 км.
Варіант 3. Найкращий результат, тобто мінімальний загальний пробіг, отримаємо, якщо збудуємо заправку на 78-му кілометрі, що відповідатиме медіані. Тоді пробіг складатиме 3820 км і 990 км. Загальний пробіг 4810 км.
Задача 6. На одному з відрізків залізниці планується створити зупинку пасажирського поїзда. Розподіл населених пунктів з чисельністю їх населення наведено в таблиці
| На якому км залізниці розташований населений пункт |
10 |
12 |
15 |
25 |
28 |
30 |
33 |
| Чисельність населення, тис. чол. |
5 |
2 |
3 |
10 |
1 |
4 |
6 |
На якому кілометрі залізниці потрібно розташувати цю зупинку, щоб сумарна відстань, яку покриватимуть потенційні пасажири до цієї зупинки, була найменшою?
Зробити висновок щодо задач.
Анкета для учнів:
Сформулювати означення термінів:
Математична статистика;
Види несуцільних спостережень;
Мода;
Медіана.
Аналіз відповідей на питання анкети та висновок: коли людину вчать – вона запам’ятовує 10% інформації, а, коли вчиться сама – 60%.
Висновок: елементи математичної статистики вивчаються не стільки для формування графічної культури та обчислювальних навичок, як для того, щоб ознайомити вас із сучасним станом науки, формувати уявлення про ідеї та методи математики та її роль у пізнанні навколишнього світу.
Завдання до уроку
Задача 1. Взуттєвикам треба знати, скільки взуття слід випускати того чи іншого розміру. Опитати всіх, тобто десятки мільйонів чоловіків і жінок, надто дорого і довго. Тому роблять вибірку: наприклад, опитали 60 жінок, їх розміри взуття записали в таблицю.
| 23.5 | 24 | 23 | 24.5 | 23 | 22.5 | 24.5 | 22.5 | 23.5 | 23.5 | 23.5 | 23.5 |
| 25.5 | 21 | 24 | 25 | 23.5 | 22 | 23 | 24.5 | 23 | 24.5 | 23 | 24.5 |
| 25 | 24 | 21.5 | 23.5 | 24.5 | 22.5 | 22 | 23.5 | 26.5 | 25.5 | 25 | 26 |
| 24 | 23 | 21 | 25 | 24.5 | 23 | 23.5 | 23.5 | 23 | 22 | 24.5 | 23.5 |
| 21.5 | 24.5 | 21.5 | 22 | 23.5 | 23 | 22 | 24.5 | 25.5 | 24.5 | 25 | 22 |
Для зручності її групують у класи (за розмірами взуття) і відмічають, скільки значень вибірки містить кожен клас.
| розмір | 21 | 21.5 | 22 | 22.5 | 23 | 23.5 | 24 | 24.5 | 25 | 25.5 | 26 | 26.5 |
| кількість |
|
|
|
|
|
|
|
|
|
|
|
|
Такі таблиці називають частотними.
Задача 2. За таблицею побудуйте гістограму розподілу учнів класу за роками народження.
| Рік народження | 1990-1991 | 1991-1992 | 1992-1993 | 1993-1994 |
| Кількість учнів | 1 | 20 | 3 | 2 |
Задача 3. Рівні води в річці Прип’ять по відношенню до номіналу вимірювали протягом 50 весняних паводків і дані вносили в таблицю:
| Рівень, см | 0-25 | 25-50 | 50-75 | 75-100 | 100-125 | 125-150 | 150-175 | 175-200 | 200-225 | 225- 250 | 250-275 | 275-300 |
| Кількість випадків | 0 | 1 | 4 | 6 | 7 | 8 | 5 | 4 | 6 | 4 | 3 | 2 |
Побудувати за цими даними гістограму та полігон частот.
Задача 4. Знайти центральні тенденції вибірки: 1,5; 1,4; 1,8; 1,5; 0; 2,1; 1,5; 2,1; 1,8 (моду, середнє значення і медіану).
Задача 5. На автостраді довжиною 100 км є 10 автостоянок. Для проектування будівництва заправки були зібрані дані про число допустимих поїздок до неї з кожної автостоянки. Результати занесені в таблицю
| На якому кілометрі Розміщена стоянка |
7 |
26 |
28 |
37 |
40 |
46 |
60 |
78 |
86 |
92 | Всього поїздок |
| Проектоване число поїздок |
10 |
15 |
5 |
20 |
5 |
25 |
15 |
30 |
10 |
65 |
200 |
Потрібно спроектувати заправку так, щоб загальний пробіг машин до неї був найменшим.
Задача 6. На одному з відрізків залізниці планується створити зупинку пасажирського поїзда. Розподіл населених пунктів з чисельністю їх населення наведено в таблиці
| На якому км залізниці розташований населений пункт |
10 |
12 |
15 |
25 |
28 |
30 |
33 |
| Чисельність населення, тис. чол. |
5 |
2 |
3 |
10 |
1 |
4 |
6 |
На якому кілометрі залізниці потрібно розташувати цю зупинку, щоб сумарна відстань, яку покриватимуть потенційні пасажири до цієї зупинки, була найменшою?
2. Сформулювати означення термінів:
2. Сформулювати означення термінів:
Завдання для індивідуальної роботи
Задача 1. 10 абітурієнтів дістали на трьох екзаменах таку кількість балів: 10;9;11;10;12;14;13;15;9;10.Побудувати статистичний розподіл цих даних, заповнивши таблицю:
| Кількість балів | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| Кількість абітурієнтів |
|
|
|
|
|
|
|
Задача 2..За даними таблиці про врожайність пшениці на різних ділянках посівної площі побудувати гістограму
| Врожайність ц/га | 20-25 | 25-30 | 30-35 | 35-40 | 40-45 | 45-50 |
| Частка ділянки від загальної посівної площі % |
5 |
10 |
33 |
21 |
25 |
6 |
Завдання для групи:
Задача 3.Програма кредитування населення у 2004 році банком”Мрія” складала:
| місяць | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Планове кредитування(тис.грн.) | 12 | 10 | 12 | 9 | 8 | 11 | 10 | 9 | 10 | 12 | 12 | 15 |
| Дійсне кредитування(тис.грн.) | 14 | 9 | 11 | 6 | 8 | 12 | 9 | 7 | 9 | 17 | 21 | 23 |
Побудувати полігон частот.Чи доцільно у даній задачі використовувати гістограму





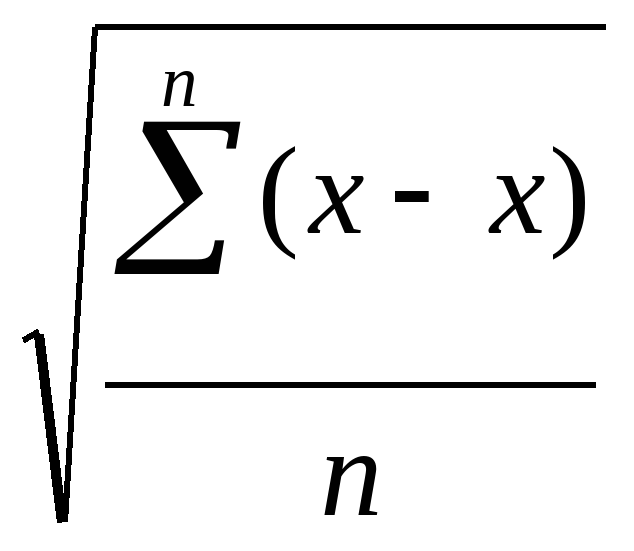 =
= 












